Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа № 4 Упрощенная процедура обработки результатов прямых измерений с многократными наблюдениямиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1 Цель работы Ознакомление с упрощенной процедурой обработки результатов прямых измерений с многократными наблюдениями. Получение, применительно к упрощенной процедуре, навыков обработки результатов наблюдений, оценивания погрешностей результатов измерений и планирования количества наблюдений. 2 Сведения, необходимые для выполнения работы Используя рекомендованную литературу, ознакомьтесь со следующими вопросами: - измерения с многократными наблюдениями; - упрощенный способ обработки и представления результатов прямых измерений с многократными, независимыми наблюдениями при наличии случайной погрешности; - правилами суммирования погрешностей; - способы получения и представления результатов измерений при наличии нескольких составляющих погрешности; - принцип действия, устройство и характеристики средств измерений, используемых при выполнении настоящей работы. Для обработки результатов многократных наблюдений могут быть использованы различные процедуры. Стандартная методика (см. работу 3) весьма трудоемка, причем, далеко не всегда можно выполнить серию наблюдений, объем которой достаточен для выявления закона распределения случайной составляющей погрешности и применения стандартной методики. Кроме того, если неисключенный остаток систематической погрешности сравнительно велик, выполнение длинной серии наблюдений для максимального уменьшения влияния случайной составляющей погрешности теряет смысл. Упрощенная процедура обработки результатов прямых измерений с многократными наблюдениями применяется, если число наблюдений n ≤30. При использовании этой процедуры за результат измерения также как и всегда принимается среднее арифметическое результатов исправленного ряда наблюдений, которое вычисляют по формуле:
где xi – i-й исправленный результат наблюдения, Для расчета среднего квадратического отклонения результата измерения S(x) используется формула:
Среднее квадратическое отклонение S(x) является основной характеристикой размера случайных погрешностей результата измерений. Для нахождения границ доверительного интервала случайной погрешности измерений в рассматриваемом случае рекомендуется проанализировать априорную информацию об объекте измерений и условиях проведения измерений. Если явно выраженных причин, способных привести к отклонению закона распределения результатов наблюдений от нормального, не выявлено, то доверительные границы находят с помощью квантилей распределения Стьюдента по формулам:
где xн и xв – соответственно координаты нижней и верхней границ доверительного интервала, t – квантиль распределения Стьюдента. Значения квантиля в зависимости от числа наблюдений n и доверительной вероятности Рд приведены таблицах. Если на результат измерений оказывает влияние только случайная составляющая погрешности, то этот результат представляют в виде: Часто имеет место ситуация, когда на результат измерений оказывают влияние две составляющие, а именно: погрешность средства измерений и случайная составляющая погрешности, зависящая от внешних факторов. Погрешность средства измерений определяется по его классу точности, а случайная – оценивается с помощью приведенной выше методики. В этом случае при определении результирующей погрешности измерений возникает задача суммирования погрешностей. В теории измерений показывается, что в случае независимых составляющих погрешности справедливо следующее соотношение:
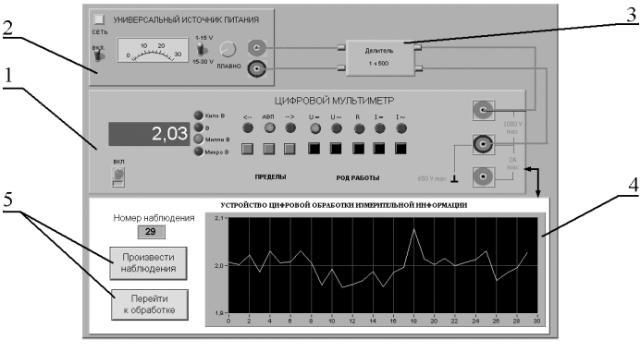
где ∆Σ – результирующая погрешность,∆1 и∆2 – составляющие погрешности, причем, если модуль одной из составляющих превышает модуль другой составляющей более чем в 8 раз, то влиянием меньшей составляющей на результирующую погрешность можно пренебречь. Если доверительная вероятность для погрешности средства измерений не указана, то при расчетах ее можно принимать равной 95%. Результат измерений представляют в виде: Видно, что по мере того, как количество наблюдений растет, вклад случайной составляющей погрешности в окончательный результат постепенно уменьшается и может настать момент, когда вклад случайной погрешности в общую погрешность измерений станет пренебрежимо мал. Ясно, что в этом случае дальнейшее увеличение количества наблюдений бессмысленно. Таким образом, измерения с многократными наблюдениями оправданы не всегда, а при их планировании полезно заранее оценить требуемый объем выборки. В противном случае трудоемкость измерений может оказаться неоправданно высокой, а увеличение точности - незначительным. 4 Описание лабораторного стенда Лабораторный стенд представляет собой LabVIEW компьютерную модель, располагающуюся на рабочем столе персонального компьютера (рис. 4.1). Оформление стенда, состав оборудования на нем, и порядок работы с ним полностью повторяют вариант, описанный в работе № 3. Схема включения приборов при выполнении работы соответствует показанной на рис. 3.2.
1-электронныйцифровой мультиметр,2-универсальныйисточник питания,3-делительнапряжения, 4- индикатор устройства обработки измерительной информации,5-элементыуправления устройством обработки измерительной информации Рисунок 4.1 – Вид модели лабораторного стенда на рабочем столе компьютера при выполнении лабораторной работы №4 4 Рабочее задание 4.1 Изучите описание работы и рекомендованную литературу. Продумайте свои действия за компьютером. 4.2 Запустите программу лабораторного практикума и выберите лабораторную работу № 1.4 в группе работ «Обработка и представление результатов измерений». На рабочем столе автоматически появится страница для выбора числа наблюдений. Самостоятельно или по указанию преподавателя выберите в интервале от 3 до 30 число наблюдений и установите выбранное значение в соответствующем окне (рис. 4.2). После этого нажмите кнопку «Продолжить». На экране компьютера появится лабораторный стенд со средствами измерений и вспомогательными устройствами (рис. 4.1) и окно лабораторного журнала, созданного в среде MS Excel. Журнал служит для формирования отчета по результатам выполнения лабораторной работы.
Рисунок 4.2 – Вид рабочего стола компьютера при выборе числа многократных наблюдений 4.3 Приготовьте к работе проверенную на отсутствие вирусов, отформатированную 3,5-дюймовуюдискету и вставьте её в дисковод. 4.4 Ознакомьтесь с расположением моделей отдельных средств измерений и других устройств на рабочем столе. 4.5 Приступите к выполнению лабораторной работы. Задание 1 Выполнение многократных независимых наблюдений в автоматическом режиме. a С помощью регулятора выходного напряжения УИП установите на его выходе напряжение в диапазоне от 1 В до 15 В. Напряжение на выходе делителя напряжение будет, соответственно, в пятьсот раз меньше. b Убедитесь, что УЦОИИ запрограммировано на выбранное ранее число наблюдений, после чего, нажатием на кнопку «Произвести наблюдения» на лицевой панели устройства, запустите режим сбора данных. УЦОИИ начнет получение измерительной информации от цифрового мультиметра, причем, результаты будут, по мере поступления, отображаться на графическом индикаторе устройства. c После окончания сбора данных изучите результаты наблюдений, представленные на графическом индикаторе. Задание 2 Выполнение автоматизированной упрощенной процедуры обработки результатов многократных независимых наблюдений. a Оцените среднее арифметическое и среднее квадратическое отклонение результатов многократных наблюдений для чего: 1 с помощью расположенной на лицевой панели УЦОИИ кнопки «Перейти к обработке» запустите режим автоматизированной упрощенной обработки ряда наблюдений (УЦОИИ проводит обработку в точном соответствии с методикой, описанной в разделе 3 настоящей работы) 2 дождитесь появления в окне УОЦИИ результатов обработки, а именно: значения среднего арифметического результатов наблюдений, оценки среднего квадратического отклонения результатов наблюдений и оценки среднего квадратического отклонения среднего арифметического результатов Наблюдений 3 запишите в отчет показания УЦОИИ, результаты обработки, а также сведения о классе точности цифрового мультиметра. b Найдите доверительные границы случайной погрешности результата измерений, длячего: 1 с помощью расположенной на лицевой панели УЦОИИ кнопки «Продолжить» запустите режим расчета границ случайной погрешности результата измерений, в ответ УЦОИИ запросит данные о выбранном значении доверительной вероятности (см. рис. 3.4); 2 выберите значение доверительной вероятности и установите его в соответствующем окне на лицевой панели УЦОИИ; 3 с помощью расположенной на лицевой панели УЦОИИ кнопки «Вычислить» запустите режим вычисления границ случайной погрешности. УЦОИИ при выбранном значении доверительной вероятности вычислит значения квантиля распределения Стьюдента и координаты границ доверительного интервала для случайной погрешности и отобразит полученный результат в соответствующем окне; 4 запишите полученные результаты в отчет. c С помощью расположенной на лицевой панели УЦОИИ кнопки «Продолжить» запустите режим вычисления инструментальной погрешности и доверительных границ погрешности результата измерений. Запишите полученные результаты в отчет. d С помощью кнопки «Продолжить» перейдите в режим сохранения массива ряда наблюдений. Для сохранения данных введите оригинальное имя файла и используйте расположенную рядом кнопку «Сохранить». Затем остановите программу при помощи кнопки «СТОП». e Запишите результат измерений в отчет и сохраните отчет с результатами работы под оригинальным именем в виде ***.XLS файла на дискете. f Дважды повторите измерения согласно п.п. a-e,каждый раз изменяя напряжение на выходе УИП и количество наблюдений. 4.6 После сохранения результатов закройте приложение LabVIEW и, при необходимости, выключите компьютер. 5 Оформление отчета Отчет должен содержать: - сведения о цели и порядке выполнения работы. - сведения об использованных методах измерений. - сведения о характеристиках использованных средств измерений. - необходимые электрические схемы. - данные, на основании которых выбирались средства измерений для выполнения каждого из пунктов задания. - экспериментальные данные. - полностью заполненные таблицы отчета (см. табл. 4.1), а также примеры расчетов, выполнявшихся при заполнении таблиц. - анализ полученных данных и вывод об особенностях и качестве проведенных измерений и результатах проделанной работы. Таблица 4.1 – Упрощенная процедура обработки результатов прямых измерений с многократными наблюдениями
6 Контрольные вопросы 1 В каких случаях проводят измерения с многократными независимыми наблюдениями? Что принимают за результат таких измерений, если количество наблюдений не превышает тридцати? 2 Когда проводится упрощенная процедура обработки результатов измерений с многократными наблюдениями, в чем она заключается? 3 Всегда ли для повышения точности результата измерений желательно проводить многократные наблюдения? Как оценить необходимое количество таких наблюдений в отдельно взятой серии? 4 Как представить результаты измерений с многократными наблюдениями? От чего зависит выбор способа представления результатов? 5 Что такое инструментальная погрешность? Всегда ли она оказывает влияние на результаты измерений? Когда ее влиянием можно пренебречь? 6 Как вычислить результирующую погрешность измерений, если на результаты одновременно влияют: - инструментальная составляющая погрешности и случайная составляющая погрешности? - неисключенный остаток систематической погрешности и случайная составляющая погрешности? - две и более систематических составляющих? 7 Какие возможности ВП были использованы при выполнении настоящей работы?
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 876; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.199.54 (0.012 с.) |

 (4.1)
(4.1) среднее арифметическое исправленного ряда наблюдений, n – число результатов наблюдений.
среднее арифметическое исправленного ряда наблюдений, n – число результатов наблюдений. (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4)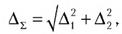 (4.5)
(4.5)