Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа № 5 Обработка результатов прямых измерений с многократными наблюдениями при наличии грубых погрешностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1 Цель работы Ознакомление с методикой выполнения прямых измерений с многократными наблюдениями при наличии грубых погрешностей (выбросов). Получение, применительно к этому случаю, навыков обработки результатов наблюдений и оценивания погрешностей результатов измерений. 2 Сведения, необходимые для выполнения работы Используя рекомендованную литературу, настоящее описание, ознакомьтесь со следующими вопросами: - процедуры обработки результатов наиболее широко используемые в практике прямых измерений с многократными наблюдениями; - критерии грубой погрешности. Методы обнаружения и исключения грубых погрешностей; - критерии согласия, используемые для проверки принадлежности результатов наблюдений к нормальному закону распределения при малом (15<n<50) количестве наблюдений; - правилами суммирования погрешностей; - принцип действия, устройство и характеристики средств измерений, используемых при выполнении настоящей работы. Для повышения качества измерений часто выполняют измерения с многократными наблюдениями, т.е. один и тот же оператор несколько раз повторяет однократные измерения в одинаковых условиях, с использованием одного и того же средства и метода измерений. После получения результатов наблюдений полученные данные обрабатывают, при этом могут быть использованы различные процедуры статистической обработки, например, стандартная или упрощенная методика (см. работы № 3 и № 4). Одним из условий правомерности статистической обработки результатов многократных наблюдений является требование однородности выборки, т.е. принадлежности всех членов выборки к одной и той же генеральной совокупности. Иными словами, если в выборке имеются наблюдения, результаты которых явно выходят за границы, обусловленные ходом эксперимента в целом, то результаты этих наблюдений следует из выборки исключить. Такие «чужие» результаты называют выбросами или промахами, а соответствующую погрешность – грубой погрешностью. Вэкспериментальной практике поиск «чужого» наблюдения основан на процедуре, которая называется «цензурированием выборки». Цензурирование выборки предполагает использование формальных критериев. Существует целый ряд таких критериев, простейший из которых известен как правило трех сигм. Всоответствии с этим правилом вычисляется оценка среднеквадратического отклонения результата измерения:
где xi –i-йисправленный результат наблюдения, Существует более квалифицированный критерий, согласно которому проверяется гипотеза о том, что сомнительный результат наблюдения xi не содержит грубой погрешности. Сомнительными в первую очередь являются наибольший xмакс или наименьший xмин из результатов наблюдений. Поэтому для проверки гипотезы пользуются статистикой При заданной доверительной вероятности Рд = α или уровне значимости q =1 −α можно найти те наибольшие значения νq, которые случайная величина ν в принципе может принять по совершенно случайным причинам. Таким образом, если вычисленное по опытным данным значение ν окажется меньше νq, то принимается гипотеза об однородности ряда наблюдений, в противном случае эту гипотезу отвергают, как противоречащую экспериментальным данным. Если ряд наблюдений неоднороден, то результат xмакс или соответственно xмин рассматривают как содержащий грубую погрешность и из дальнейшего рассмотрения исключают. Отметим, что в q =1−α доле случаев из ста мы можем допустить ошибку первого рода, т.е. принять за неоднородную выборку, которая на самом деле является однородной. Важно, что удалять промахи из выборки более одного раза не рекомендуется. После удаления промахов обработка результатов наблюдений ведется обычным образом (см. работы № 3 и № 4). Следует особо упомянуть о том, что упомянутые критерии грубых погрешностей работают только при условии, если распределение результатов наблюдений подчиняется нормальному закону. При небольшом числе наблюдений 15<n<50 критерий Пирсона не работает и для проверки гипотезы о принадлежности результатов наблюдений к нормальному распределению можно использовать тот факт, что и коэффициент асимметрии и эксцесс для нормального распределения равны нулю. Эмпирическая оценка Γ1 коэффициента асимметрии находится по формуле:
Эмпирическая оценка Γ2 эксцесса находится по формуле:
Степень рассеяния для величин Γ1 иΓ2 может быть приближенно оценена путем сравнения их с оценкой среднего квадратического отклонения коэффициентов асимметрии σΓ1 и эксцесса σΓ2:
Распределение считают нормальным, если одновременно выполняются соотношения:
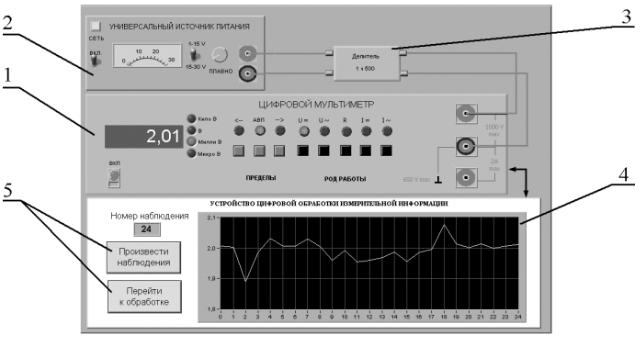
В случае если число результатов наблюдений n ≤15, принадлежность их к нормальному распределению с помощью критериев согласия не проверяют. 3 Описание лабораторного стенда Лабораторный стенд представляет собой LabVIEW компьютерную модель, располагающуюся на рабочем столе персонального компьютера (рис. 5.1). Оформление стенда, состав оборудования на нем и порядок работы с ним полностью повторяют вариант, описанный в работе № 3. Схема включения приборов при выполнении работы изображена на рис. 3.2.
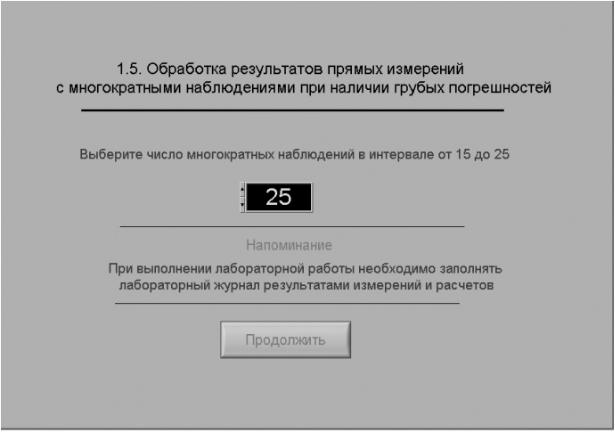
1-электронныйцифровой мультиметр,2-универсальныйисточник питания,3-делительнапряжения, 4- индикатор устройства обработки измерительной информации,5-элементыуправления устройством обработки измерительной информации Рисунок 5.1 – Вид модели лабораторного стенда на рабочем столе компьютера при выполнении лабораторной работы № 5 4 Рабочее задание 4.1 Изучите описание работы и рекомендованную литературу. Продумайте свои действия за компьютером. 4.2 Запустите программу лабораторного практикума и выберите лабораторную работу № 1.5 в группе работ «Обработка и представление результатов измерений». На рабочем столе автоматически появится страница для выбора числа наблюдений. Самостоятельно или по указанию преподавателя выберите в интервале от 15 до 25 число наблюдений и установите выбранное значение в соответствующем окне (рис. 5.2). После этого нажмите кнопку «Продолжить». На экране компьютера появится лабораторный стенд со средствами измерений и вспомогательными устройствами (рис. 5.1) и окно лабораторного журнала, созданного в среде MS Excel. Журнал служит для формирования отчета по результатам выполнения лабораторной работы.
Рисунок 5.2 – Вид рабочего стола при выборе числа многократных наблюдений 4.3 Приготовьте к работе проверенную на отсутствие вирусов, отформатированную 3,5-дюймовуюдискету и вставьте её в дисковод. 4.4 Ознакомьтесь с расположением моделей отдельных средств измерений и других устройств на рабочем столе. 4.5 Приступите к выполнению лабораторной работы. Задание 1 Выполнение многократных независимых наблюдений в автоматическом режиме. a С помощью регулятора выходного напряжения УИП установите на его выходе напряжение в диапазоне от 1 В до 15 В. Напряжение на выходе делителя напряжение будет, соответственно, в пятьсот раз меньше. b Убедитесь, что УЦОИИ запрограммировано на выбранное ранее число наблюдений, после чего, нажатием на кнопку «Произвести наблюдения» на лицевой панели устройства, запустите режим сбора данных. УЦОИИ начнет получение измерительной информации от цифрового мультиметра, причем, результаты будут, по мере поступления, отображаться на графическом индикаторе устройства. c После окончания сбора данных изучите результаты наблюдений, представленные на графическом индикаторе.
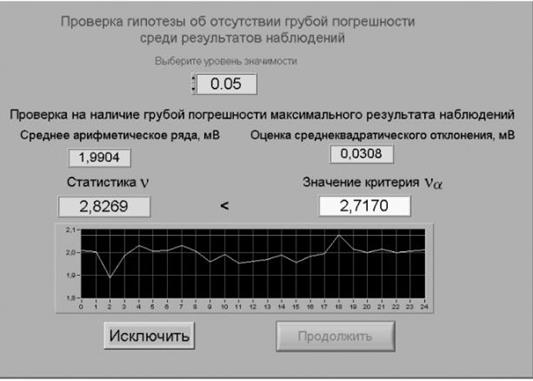
Рисунок 5.3 – Вид рабочего стола при проверке гипотезы об отсутствии грубой погрешности среди результатов наблюдений Задание 2 Выполнение автоматизированной процедуры исключения результатов многократных независимых наблюдений, содержащих грубые погрешности. a Проверьте гипотезу об отсутствии среди полученных результатов наблюдений грубой погрешности, для чего: 1 выберите уровень значимости для проверки гипотезы и установите его в соответствующем окне на лицевой панели УЦОИИ; 2 с помощью расположенной на лицевой панели УЦОИИ кнопки «Перейти к обработке» запустите режим автоматизированной обработки ряда наблюдений (УЦОИИ проводит обработку в точном соответствии с методикой, описанной в разделе 3 настоящей работы); 3 дождитесь появления в окне УЦОИИ результатов обработки, а именно: значения среднего арифметического результатов наблюдений, оценки среднего квадратического отклонения результатов наблюдений, статистики ν и значения критерияνq (см. рис. 5.3). Если значение статистики ν оказывается меньше значения критерия νq, то максимальное значение ряда наблюдений не содержит грубой погрешности; 4 при наличии грубой погрешности нажмите кнопку «Исключить». В результате максимальное значение будет исключено из ряда и среднее арифметическое, оценка среднего квадратического отклонения ряда наблюдений и статистика ν будут рассчитаны заново; 5 запишите полученные результаты в отчет и нажмите кнопку «Продолжить».
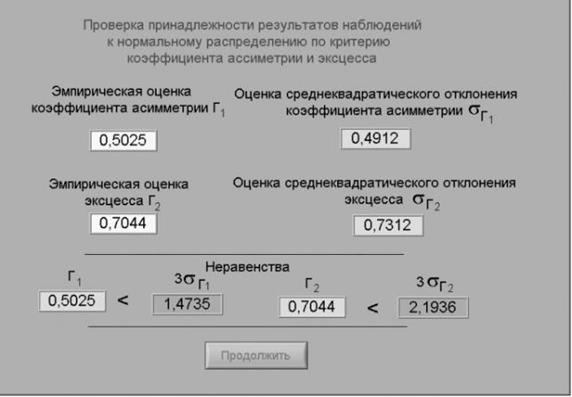
Рисунок 5.4 – Вид рабочего стола при проверке гипотезы о принадлежнрости результатов наблюдений к нормальному распределению по критерию коэффициента асимметрии и эксцесса b Повторите процедуру, описанную в пункте a, для минимального из полученных результатов наблюдений. Задание 3 Выполнение автоматизированной процедуры проверки принадлежности результатов многократных независимых наблюдений к нормальному распределению и получение результатов измерения. a На следующей странице осуществляется проверка принадлежности результатов наблюдений нормальному распределению по критериям коэффициента асимметрии и эксцесса (см. рис. 5.4). Для этого по формулам 5.2 – 5.5 рассчитываются: 1) эмпирическая оценка коэффициента асимметрии Γ1; 2) эмпирическая оценка эксцесса Γ2; 3) оценка среднего квадратического отклонения коэффициента асимметрии σΓ1; 4) оценка среднего квадратического отклонения эксцесса σΓ2. b Если неравенства выполняются (см. формулы 5.6 и 5.7), то гипотезу о нормальном распределении следует принять. c Внесите необходимые величины в лабораторный журнал и нажмите кнопку «Продолжить». d На очередной странице программа производит расчет доверительных границ случайной погрешности результата измерений (см. рис. 3.4). Для определения доверительных границ необходимо выбрать доверительную вероятность и затем нажать кнопку «Вычислить». Внесите значения доверительной вероятности, квантиля распределения Стьюдента и доверительные границы случайной погрешности в лабораторный журнал и нажмите кнопку «Продолжить». e На следующей странице на основе сведений о погрешности цифрового мультиметра сначала вычисляется инструментальная погрешность. Затем находится отношение погрешности средства измерения к ширине доверительного интервала, после чего находятся доверительные значения погрешности результата измерения. Перечисленные значения должны быть занесены в лабораторный журнал. f С помощью кнопки «Продолжить» перейдите в режим сохранения массива ряда наблюдений. Для сохранения данных введите оригинальное имя файла и используйте расположенную рядом кнопку «Сохранить». Затем остановите программу при помощи кнопки «СТОП». g Запишите результат измерений в отчет и сохраните отчет с результатами работы под оригинальным именем в виде ***.XLS файла на дискете. h Дважды повторите измерения согласно п.п. a-g,каждый раз изменяя напряжение на выходе УИП и количество наблюдений. 4.6 После сохранения результатов закройте приложение LabVIEW и, при необходимости, выключите компьютер. 5. ОФОРМЛЕНИЕ ОТЧЕТА Отчет должен содержать: - сведения о цели и порядке выполнения работы; - сведения об использованных методах измерений; - сведения о характеристиках использованных средств измерений; - необходимые электрические схемы; - данные, на основании которых выбирались средства измерений для выполнения каждого из пунктов задания; - экспериментальные данные; - полностью заполненные таблицы отчета (см. табл. 5.1), а также примеры расчетов, выполнявшихся при заполнении таблиц; - анализ полученных данных и вывод об особенностях и качестве проведенных измерений и результатах проделанной работы. Таблица 5.1 – Обработка результатов прямых измерений с многократными наблюдениями при наличии грубых погрешностей
6 Контрольные вопросы 1 Что такое грубые погрешности? Как устранить их влияние на результат измерений? 2 Какие критерии согласия используют при обработке результатов многократных наблюдений, если предполагается наличие грубых погрешностей? 3 Каковы преимущества и недостатки правила «трех сигм»? 4 Сколько раз рекомендуется устранять грубые погрешности из выборки? 5 Как обрабатывают результаты наблюдений после устранения грубых погрешностей?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 1535; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

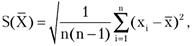 (5.1)
(5.1) – среднее арифметическое исправленного ряда наблюдений, n – число результатов наблюдений. Далее граница цензурирования назначается в виде |хгр −
– среднее арифметическое исправленного ряда наблюдений, n – число результатов наблюдений. Далее граница цензурирования назначается в виде |хгр −  ), после чего все |хгр −
), после чего все |хгр −  или
или 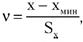 где
где  - оценка среднего квадратического отклонения ряда наблюдений. Соответствующие функции распределения совпадают между собой и протабулированы для нормального закона распределения результатов наблюдений.
- оценка среднего квадратического отклонения ряда наблюдений. Соответствующие функции распределения совпадают между собой и протабулированы для нормального закона распределения результатов наблюдений.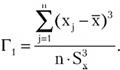 (5.2)
(5.2) (5.3)
(5.3)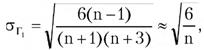 (5.4)
(5.4)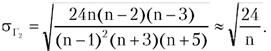 (5.5)
(5.5)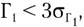 (5.6)
(5.6) (5.7)
(5.7)