
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов измерения токаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
2.4.3.1. Записать результат с учётом инструментальной погрешности.
2.4.3.2. Найти методическую погрешность:
2.4.3.3. Определить поправку и погрешность поправки:
2.4.3.4. Результат с учётом инструментальной и методической погрешности записывается в виде:
2.5. Содержание отчета : 1. Цель работы. 2. Схема измерения. 3. Таблицы и графики результатов измерения. 4. Результаты обработки эксперимента. 5. Выводы и замечания по работе. 2.6. Контрольные вопросы: 1. Прямые и косвенные измерения. 2. Совместные и совокупные измерения. 3. Истинное, действительное и измеренное значения физической величины. 4. Как рассчитать абсолютную и относительную погрешности? 5. Что такое класс точности прибора? 6. Причины возникновения методических погрешностей. 7. Как рассчитать методическую погрешность измерения напряжения тока? ЛАБОРАТОРНА РОБОТА №3 Цель работы: ознакомиться с измерительными приборами; изучить методику измерений сопротивления прямым и косвенным методами и определения их погрешностей. Теоретические сведения (приведены в лабораторной работе №2)
Подготовка приборов к измерению сопротивления 3.2.1. В7-26
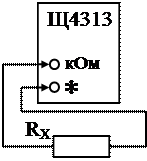
3.2.2. Щ4313 Переключатель рода работ выставить в положение «
3.3.1 На магазине сопротивлений установить:
3.3.2. Подключить RX к В7-26 (рис.2) и измерить его величину. Конечное значение шкалы Rk = 3.3.3. Подключить RX к Щ4313 (рис.3) и измерить его величину.Записать значения Rизм, Rk, коэффициентов a и b (см. паспорт прибора), вычислить класс точности KП прибора. Для мультиметра Щ4313 класс точности определяется по формуле:
3.3.4. С учетом инструментальной погрешности результат измерений прибором В7-26 записать в виде:
где Rизм – измеренное значение, RK – конечное значение шкалы прибора. 3.3.5. Результат измерений прибором Щ4313 записать в виде:
3.3.6. На магазине сопротивлений установить R2 = (кОм) и выполнить пункты 2.1. - 2.5.
3.4. Измерение сопротивлений R1 и R2 косвенным методом
3.4.1. Собрать схему (рис. 4). Установить на источнике питания Е = (В).
Записать результат измерения сопротивлений R1(R2) с учетом инструментальной погрешности косвенных измерений:
Методическая погрешность измерений:
Окончательный результат измерения сопротивления:
3.4.2. Собрать схему (рис. 5). Записать результаты измерений тока и напряжения:
Записать результат измерения с учетом инструментальной погрешности косвенных измерений:
Методическая погрешность измерений:
Поправка на методическую погрешность:
Случайная погрешность поправки
Результат измерения сопротивления с учетом погрешностей:
5. По полученным результатам сделать выводы. 3.4. Содержание отчета: 1. Цель работы. 2. Схема измерения. 3. Таблицы и графики результатов измерения. 4. Результаты обработки эксперимента. 5. Выводы и замечания по работе. 3.5. Контрольные вопросы: 1. Как измерить сопротивление резистора методом амперметра-вольтметра? Как при этом определить погрешность измерения сопротивления? 2. Как определить методическую погрешность измерения сопротивления методом амперметра-вольтметра? 3. Как определить погрешность измерения сопротивления омметром? ЛАБОРАТОРНА РОБОТА №4 Цель работы: изучить порядок обработки результатов многократных, равноточных наблюдений при прямых измерениях; приобрести навыки стандартной обработки результатов наблюдений, оценки погрешностей и способов представления результатов измерений. Теоретические сведения В измерительной практике для уменьшения влияния случайных погрешностей на результат измерения проводят измерения с многоразовыми наблюдениями, а затем статистически обрабатывают полученные результаты. При этом могут быть использованы различные процедуры обработки. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. Результат измерения содержит погрешность, представляющую сумму систематической составляющей DС и случайной составляющей
Эти две составляющие погрешности резко отличаются по своим свойствам. Систематическая погрешность DС остается постоянной или изменяется по определенному закону при повторных измерениях одной и той же физической величины. Она является математическим ожиданием
Обнаружение систематической погрешности – трудоемкая операция и может быть выполнена несколькими способами: 1) Проверка данного измерительного прибора с помощью образцового (более точного). При измерении одной и той же физической величины измерительным и образцовым приборами получают разные показания: X раб и X обр. Их разность является абсолютной систематической погрешностью прибора:
Тогда показания рабочего прибора корректируются введением поправки П, численно равной
При этом за результат измерения необходимо принимать величину
2) Метод замещения. В этом случае измеряемая величина 3) Метод компенсации по знаку применяется при направленном действии причины, вызывающей систематическую погрешность. Выполняют измерения так, чтобы погрешность входила с разными знаками в формулы
тогда Переменные систематические погрешности разделяют на прогрессирующие и периодические. Для устранения этих составляющих необходимо найти функциональную связь погрешности и влияющего фактора и вводить поправку на основании полученных зависимостей. Сложную задачу по выявлению и исключению систематической погрешности не всегда удается довести до конца и поэтому остается неисключенная часть систематической погрешности. Нетрудно убедиться, что результат измерения – случайная величина. Таким образом, случайная погрешность Одной из важнейших характеристик случайной погрешности является закон распределения плотности вероятности – плотность распределения вероятностей Законы распределения могут быть дискретными (для дискретных случайных величин) и непрерывными (для непрерывных величин). Дискретный закон распределения представляет совокупность значений случайной величины
Для непрерывных случайных величин с известным законом распределения
Условие нормировки для непрерывной случайной величины имеет вид:
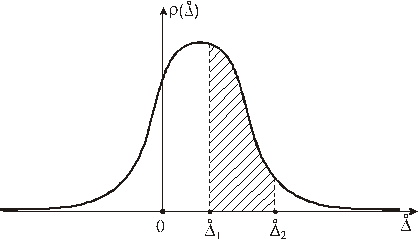
Рисунок 4.1 – Нормальный закон распределения
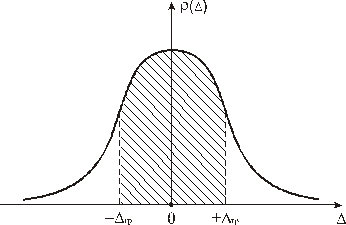
Если дестабилизирующих факторов, обуславливающих случайную погрешность много (3 и более), то закон распределения плотности вероятности
Из представленного графика видно: если в состав погрешности входит систематическая составляющая
достигается при
а) б) Рисунок 4.2 – Кривые Гаусса а) для разных значений систематической составляющей погрешности б) для разных значений среднеквадратического отклонения s. Характер закона распределения изменяется в зависимости от параметров s и s2 (рис. 4.2, б). Дисперсия
характеризует рассеяние случайной величины относительно среднего значения. Среднеквадратическое значения отклонения (СКО)
Дисперсия и СКО характеризуют точность измерений. Чем больше s2 и s, тем меньше точность, т.е. больше погрешность измрений. При нормальном законе распределения с
При введении нормированной случайной переменной
где Ф(z) – интеграл вероятности. Доверительная вероятность P дов при заданных граничных значениях погрешности – это вероятность нахождения случайной величины
Рисунок 4.3 – Доверительная вероятность при заданных граничных значениях погрешности Функция Ф(z) табулирована или определяется по графику (рис. 4.4).
Рисунок 4.4 – Функция Лапласа для разных значений нормированной переменной Если задана P дов, то по графику или таблице находят z гр, затем определяют Dгр = z гр×s. Доверительный интервал Dдов = –Dгр … +Dгр, он с заданной вероятностью накрывает истинное значение В зависимости от целей измерений доверительную вероятность на практике устанавливают Р дов = 0,95 … 0,99. За максимальное значение погрешности, описываемой нормальным законом распределения Вероятность того, что погрешность превысит максимальное значение, определяется выражением:
означающим, что погрешность в 369 случаях из 370 попадает в интервал ±3s и лишь в одном случае выходит за эти пределы.
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 847; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

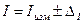 .
. .
. ;
; 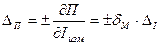 .
.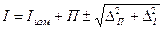 .
. Переключатель рода работ перевести в положение «r» и проверить нулевое положение указателя при замкнутых накоротко гнездах «r» и «*» (рис. 3.1). Затем разомкнуть гнезда и установить указатель (стрелку) в положение «∞» на шкале
Переключатель рода работ перевести в положение «r» и проверить нулевое положение указателя при замкнутых накоротко гнездах «r» и «*» (рис. 3.1). Затем разомкнуть гнезда и установить указатель (стрелку) в положение «∞» на шкале  ручкой «Устан. “∞”» (для
ручкой «Устан. “∞”» (для  ». Выбрать шкалу прибора.
». Выбрать шкалу прибора.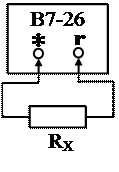 3.3. Измерение сопротивлений прямым методом
3.3. Измерение сопротивлений прямым методом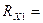 (Ом),
(Ом), 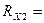 (кОм).
(кОм).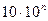 Ом (10n – множитель шкалы). Записать Rизм, Rk, KП.
Ом (10n – множитель шкалы). Записать Rизм, Rk, KП.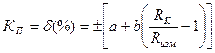 .
.
 ,
,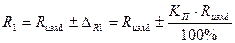 .
.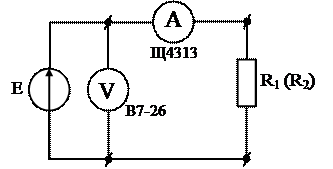
 ,. RV = 30 МОм, IK – конечное значение шкалы. Записать результаты измерений тока и напряжения в виде:
,. RV = 30 МОм, IK – конечное значение шкалы. Записать результаты измерений тока и напряжения в виде: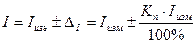 ,
,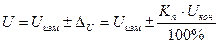 .
.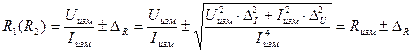 .
.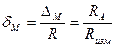 ,
,  . Поправка П = -RA.
. Поправка П = -RA.

 .
. .
.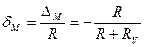 ;
;  .
.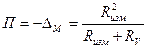 .
.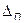 :
: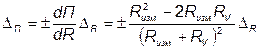 .
.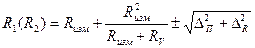 .
. :
: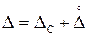 .
.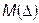 погрешности D измерения
погрешности D измерения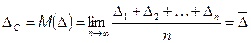 .
.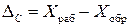 .
.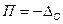 .
.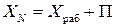 .
.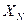 заменятся известной величиной
заменятся известной величиной 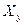 таким образом, чтобы показание прибора осталось неизменным. Тогда результат измерения
таким образом, чтобы показание прибора осталось неизменным. Тогда результат измерения  .
. ;
; 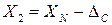 ,
,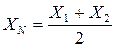 .
.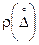 или
или  – функция распределения вероятностей.
– функция распределения вероятностей.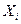 и соответствующих им вероятностей
и соответствующих им вероятностей  . Условие нормировки закона распределения вероятностей дискретной случайной величины:
. Условие нормировки закона распределения вероятностей дискретной случайной величины: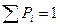 .
. вероятность того, что данная случайная величина
вероятность того, что данная случайная величина 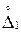 до
до  , определяется площадью, ограниченной этой кривой и осью абсцисс (рис. 4.1), т.е.
, определяется площадью, ограниченной этой кривой и осью абсцисс (рис. 4.1), т.е.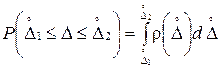 .
.
 .
.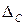 , то закон распределения плотности вероятности будет смещен на эту величину. Если же систематическая погрешность исключена
, то закон распределения плотности вероятности будет смещен на эту величину. Если же систематическая погрешность исключена 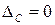 (М[D] = 0), то
(М[D] = 0), то  и максимальное значение такой кривой Гаусса
и максимальное значение такой кривой Гаусса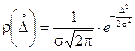
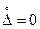 (рис. 4.2.б).
(рис. 4.2.б).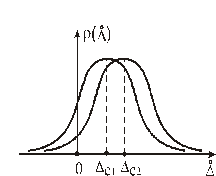
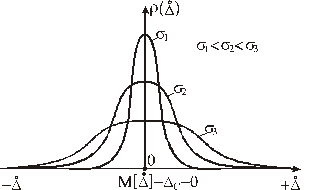
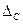
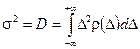
 .
. .
.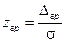 выражение P (D) преобразуется к виду:
выражение P (D) преобразуется к виду: ,
,

 , Р дов = …
, Р дов = …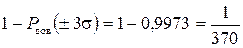 ,
,


