
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы метрологии и измеренийСодержание книги
Поиск на нашем сайте ОСНОВЫ МЕТРОЛОГИИ И ИЗМЕРЕНИЙ
Учебное пособие
Казань 2002 .
УДК 621.317.7 (077)
Мартынов Е.В. Основы метрологии и измерений: Учебное пособие. Казань: 2012. 57с. ISBN
В учебном пособии рассмотрены основные метрологические характеристики средств измерений, методы измерений, систем единиц физических величин, вопросы обеспечения точности и единства измерений, организации государственной метрологической службы. Изложена методика подготовки и проведения метрологического эксперимента. Рассмотрена методики планирования и обработки результатов эксперимента, оценки статистических характеристик результатов эксперимента, построения аналитических моделей измерительных устройств и систем по результатам метрологического эксперимента. Предназначено для студентов инженерных специальностей технических вузов.
ISBN
Содержание
ВВЕДЕНИЕ ГЛАВА 1. термины и определения……………………………………4 ГЛАВА 2. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ…………………..……. 8 Глава 3. ХАРАКТЕРИСТИКИ СРЕДСТВ измерений…………….… 13 ГЛАВА 4.ГОСУДАРСТВЕННАЯ МЕТРОЛОГИЧЕСКАЯ СЛУЖБА…….18 Глава 5. Планирование и проведение физического метрологического эксперимента для построения аналитических моделей измерительных устройств и систем............................................................................................................................... 24 Глава 6. Оценка статистических характеристик результатов эксперимента, определение точности полученных результатов................................................................................................. 34 Глава 8. Обобщение методов вычисления размерных коэффициентов аналитических моделей измерительных устройств и систем на многофакторный эксперимент. 47 Глава 9. Проверка адекватности модели............................... 49 ПРИЛОЖЕНИЯ................................................................................................ 53 1. Значения t -критерия Стьюдента при 5%-ном уровне значимости (фрагмент). 53 2. Значения G -распределения Кохрена в зависимости от чисел степеней свободы v 1, v 2 при 5%-ном уровне значимости (фрагмент)......................................... 54 3. Значения F -распределения Фишера в зависимости от чисел степеней свободы v 1, v 2 при 5%-ном уровне значимости (фрагмент)............................................. 55 СПИСОК ЛИТЕРАТУРЫ................................................................................ 57
Введение. Развивая материальное производство, человеческое общество создало науку об измерениях - метрологию. Метрология решает задачи обеспечения единства и точности измерений, унификации единиц измерения физических величин. Настоящее пособие ориентировано на студентов технических специальностей и посвящено основам измерения физических величин, характеризующих состояние технических устройств и систем. Глава 1. Термины и определения.
Метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. Различают предметные области метрологии. Теоретическая метрология – раздел метрологии, предметом которого является разработка фундаментальных основ теории методов и технических средств обеспечения необходимой точности и единства измерений. Законодательная метрология – раздел метрологии, предметом которого является установление обязательных юридических требований к применению методов и технических средств обеспечения необходимой точности и единства измерений в интересах общества и государства. Прикладная метрология – раздел метрологии, предметом которого являются вопросы применения на практике разработок теоретической метрологии и законодательной метрологии. Физическая величина – одно из свойств материальнного объекта (материальной системы, явления или процесса), общее в качественном отношении для многих объектов, но в количественном отношении индивидуальное для каждого из них. Размером физической величины называют количественную оценку физической величины, присущую конкретному материальному объекту, системе, явлению или процессу. Значение физической величины - представление размера физической величины в виде некоторого числа единиц измеренияфизической величины. Измерение – процесс определения количественных характеристик окружающегомира (значений физических величин) и действующих в природе закономерностей.
Истинное значение физической величины - значение физической величины, идеальным образом характеризующее в количественном отношении соответствующую физическую величину. Истинное значение на практике недостижимо. Оно может быть получено только в результате бесконечного числа измерений с бесконечно высокой точностью. Поэтому на практике истинное значение физической величины заменяют его оценкой – действительным значением физической величины. Действительным значением физической величины считают значение физической величины полученное экспериментальным путем с точностью достаточной для решаемой измерительной задачи, которое используется вместо истинного значения физической величины. Системой физических величин называют совокупность физических величин, используемую для описания на языке математических моделей раздела или области науки и техники и образованную двумя группами величин: группой основных физических величин, условно принятых независимыми, и группой производных физических величин, определяемых через основные величины на основании уравнений связи физических величин. Алгоритм выбора основных величин условно сводится к следующим операциям. Из группы физических величин, образующих систему, выделяют в отдельную подгруппу физические величины (основные физические величины), число которых равно разности между числом физических величин входящих в систему и числом независимых уравнений связи между ними. Персональный выбор физических величин в качестве основных не имеет теоретического обоснования, при их выборе руководствуются качественными критериями эффективности и целесообразности использования выбранных основных величин на практике. Размерность физических величин – выражение составленное из произведений символов основных физических величин и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе величин за основные. В соответствие с международными стандартами ИСО 31/0, размерность величин следует обозначать знаком dim (dim – от лат. dimension (размерность)). Размерность производной физической величины выражается через размерность основных физических величин с помощью степенного одночлена: dim X = L a × M b × T g …, где L, М, Т – размерности соответствующих основных физических величин; a,b,g - показатели степени, в которую возведены размерности основных физических величин. Единица измерения физической величины – размер физической величины, которому условно присвоено числовое значение 1. Система единица физических величины – совокупность основных и производных единиц физических величин, образованная в соответствии с принятыми принципами для заданной системы физических величин. Основная единица системы единиц физических величин – единица основной физической величины в заданной системе единиц. Производная единица системы единиц физических величин – единица производной физической величины системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами или же с основными и уже определенными производными. В качестве основных выбирают величины, вторые характеризуют фундаментальные свойства материального мира. Механика базируется на трех основных величинах, теплотехника – на четырех, физика – на семи. ГОСТ 8.417 устанавливает семь основных физических величин – длина, масса, время, термодинамическая температура, количество вещества, сила света, сила электрического тока, с помощью которых создается все многообразие производных физических величин и обеспечивается описание любых свойств физических объектов и явлений, единицы этих физических величин являются основой системы единиц СИ. Различают системные и внесистемные единицы физических величин. Системными единицами считают основные, производные, кратные и дольные единицы, входящие в систему единиц. Внесистемной считается единица физической величины не входящая в принятую систему единиц, например в систему СИ. Внесистемные единицы, разделяют на четыре группы: допускаемые к применению наравне с единицами СИ; допускаемые к применению в специальных областях; временно допускаемые и устаревшие (не допускаемые к применению). Шкала физической величины - упорядоченная совокупность значений физической величины. Простейший способ получения информации, который позволяет составить некоторое представление о размере измеряемой величины, заключается в сравнении его с другим по принципу «что больше (меньше)?» или «что лучше (хуже)?». При этом число сравниваемых между собой размеров может быть достаточно большим. Расположенные в порядке возрастания или убывания размеры измеряемых величин образуют шкалы порядка. Операция расстановки размеров в порядке их возрастания или убывания с целью получения измерительной информации по шкале порядка называется ранжированием. Для обеспечения измерений по шкале порядка некоторые точки на ней можно зафиксировать в качестве опорных (реперных). Точкам шкалы могут быть присвоены цифры, часто называемые баллами. Знания, например, оценивают по четырехбалльной реперной шкале, имеющей следующий вид: неудовлетворительно, удовлетворительно, хорошо, отлично. По реперным шкалам измеряются твердость минералов, чувствительность пленок и другие величины (интенсивность землетрясений измеряется по двенадцатибалльной шкале, называемой международной сейсмической шкалой). Второй тип шкалы – шкала интервалов. Примером ее может служить шкала измерения времени, которая разбита на крупные интервалы (годы), равные периоду обращения Земли вокруг солнца; на более мелкие (сутки), равные периоду обращения Земли вокруг своей оси. По шкале интервалов можно судить не только о том, что один размер больше другого, но и том, на сколько больше. Наиболее совершенной является шкала отношений. Примером ее может служить температурная шкала Кельвина. В ней за начало отсчета принят абсолютный нуль температуры, при котором прекращается тепловое движение молекул, более низкой температуры быть не может. Второй реперной точкой служит температура таяния льда. По шкале Цельсия интервал между этими реперами равен 273,16 °С. По шкале отношений можно определить не только, на сколько один размер больше или меньше другого, но и во только раз больше или меньше. В зависимости от того, на какие интервалы разбита шкала, один и тот же размер представляется по-разному. Например, длина перемещения некоторого тела на 1 м может быть представлена как L = 1 м = 100 см = 1000 мм. Отмеченные три варианта являются значениями измеряемой величины – оценками размера физической величины в виде некоторого числа принятых для нее единиц. Входящее в него отвлеченное число называется, числовым значением. В приведенном примере это 1, 100, 1000. Измерение – совокупность операций, выполняемых с помощью технического средства, хранящего единицу величины, позволяющего сопоставить измеряемую величину с ее единицей и получить значение величины. Это значение называют результатом измерений. Например, прикладывая линейку с делениями к какому-либо предмету, сравнивают размер предмета с единицей, хранимой линейкой, и, произведя отсчет, получают значение величины (длины, высоты и других параметров). Значение физической величины получают в результате ее измерения или вычисления в соответствии с основным уравнением измерения:
Q = X [ Q ], (2)
где Q, – значение физической величины; Х – числовое значение измеряемой величины в принятой единице; [ Q ] –выбранная для измерения единица. Погрешность измерений – отклонение результата измерений от истинного (действительного) значения измеряемой величины. Средство измерений – техническое устройство, предназначенное для осуществления измерений. Эталон единицы величины – средство измерения, предназначенное для воспроизведения и хранения единицы величины с точностью достижимой при современном уровне развития науки и техники с целью передачи единицы величины образцовым и рабочим средствам измерений данной величины. Единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений известны с заданной вероятностью. В большинстве стран мира, узаконенными единицами являются единицы величин Международной системы единиц, принятой Генеральной конференцией по мерам и весам, рекомендованные Международной организацией законодательной метрологии. Главным нормативным актом по обеспечению единства измерений в Российской Федерации является Закон Российской Федерации «Об обеспечении единства измерений». Единство измерений в государственном масштабе обеспечивает метрологическая служба. Метрологическая служба - это сеть организаций и отдельных подразделений, на которые возложена ответственность за обеспечение единства измерений. Различают государственную метрологическую службу, метрологические службы государственных органов управления и метрологические службы юридических лиц (ведомств). Одним из основных видов деятельности метрологической службы является обеспечение и проведение поверки средства измерений. Поверка средства измерений – совокупность операции, выполняемых органами государственной метрологической службы (другими уполномоченными на то органами, организациями) с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям. Передача размера единиц.
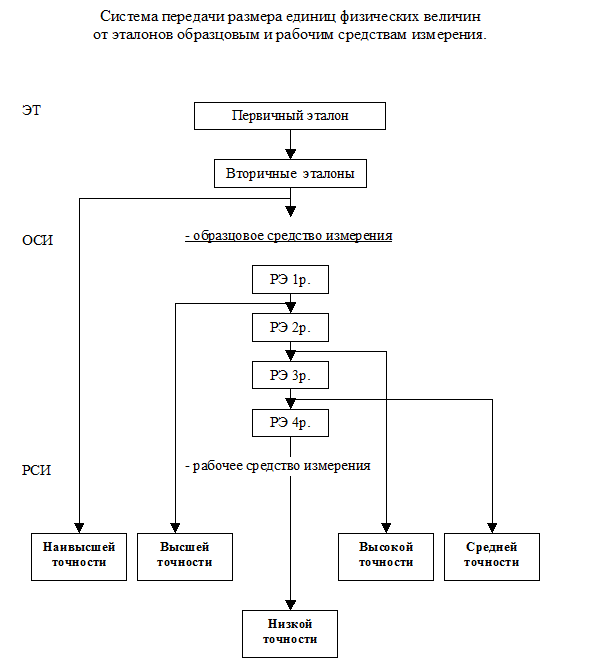
Передача размера единицы представляет собой приведение размера единицы физической величины, хранимой поверяемым СИ, к размеру единицы, воспроизводимой эталоном. При передаче информации о размере единиц СИ используют многоступенчатую процедуру. По размеру единицы, воспроизводимому государственным эталоном, устанавливаются значения единицы, воспроизводимой вторичными эталонами. Среди вторичных эталонов различают: эталоны-сравнения, применяемые для сличения эталонов, которые по тем или иным причинам не могут непосредственно сличаться друг с другом; эталоны-свидетели, предназначенные для поверки сохранности и неизменности государственного эталона и для замены его в случае порчи или утраты; эталоны-копии, используемые для передачи информации о размере единицы рабочим эталонам. Самым распространенными по численности парка вторичными эталонами являются рабочие эталоны – 1, 2, 3-го (иногда 4-го) разрядов. От рабочих эталонов низшего разряда размер передаётся рабочим средствам измерения (РСИ). Число РСИ по каждому из видов измерений достигает сотен тысяч и более (например, термометры, манометры). Наиболее точные РСИ поверяются от вторичных эталонов или рабочих эталонов 1-го разряда; наименее точные – от эталонов низшего разряда (3-го или 4-го). В качестве метода передачи размера единиц используют метод непосредственного сличения.
Рис.6 На каждой ступени передачи размера единицы точность теряется. Поэтому для высокоточных СИ сличение или поверка ведется с рабочими эталонов 1-го разряда. Документ, который устанавливает соподчинение СИ, участвующих в передаче размера единицы от эталона к рабочим СИ с указанием методов и погрешности при передаче называют поверочной схемой СИ. Различают государственные и локальные поверочные схемы. Государственные схемы регламентируют передачу информации о размере единицы парку СИ. Во главе этой схемы находится государственный эталон. Государственные поверочные схемы закладываются в основу государственных стандартов. Локальные поверочные схемы распространяются на СИ, подлежащие поверке, организуемой метрологической службой министерства (ведомства) или юридического лица. Нормативная база метрологии
Комплекс нормативных документов, устанавливающих правила, нормы, требования, направленные на достижение и поддержание единства измерений в стране при требуемой точности, составляет государственную систему обеспечения единства измерений. К системе относятся: Федеральный закон Российской Федерации от 26 июня 2008 г. N 102-ФЗ "Об обеспечении единства измерений". Государственные стандарты (ГОСТ, ГОСТ Р) системы обеспечения единства измерений. Правила государственной системы обеспечения единства измерений, утверждаемые Госстандартом РФ. Рекомендации (гриф «МИ») государственной системы обеспечения единства измерений, разрабатываемые государственными метрологическими научными центрами.
Процедуру соблюдения правил законодательной метрологии обеспечивает комплекс нормативных документов, которые регламентирует государственный метрологический контроль за: утверждением типа средств измерений, поверкой средств измерений, в том числе эталонов, лицензированием деятельности юридических и физических лиц по изготовлению, ремонту, продаже и прокату средств измерений. Процедуру утверждения типа проводят для новых СИ, предназначенных для производства или ввоза по импорту. Процедура предусматривает обязательные испытания СИ на соответствие, государственную регистрацию, выдачу сертификата об утверждении типа. Испытания проводятся государственными научными метрологическими центрами, аккредитованными в качестве государственных центров испытаний СИ (ГЦИ СИ). Утвержденный тип СИ вносится в Государственный реестр, который ведет Госстандарт. На СИ утвержденного типа и эксплуатационные документы, сопровождающие каждый экземпляр, наносится знак утверждения типа установленной формы (рис. 8). Знаки в метрологии: а – знак утверждения типа, б – поверительное клеймо, в – знак системы добровольной сертификации.
Рис.8
Каждый экземпляр СИ при выпуске из производства или ремонта, при ввозе по импорту подлежит поверке органами государственного метрологического контроля. В соответствии с международными соглашениями, заключенными Россией с другими странами, Госстандартом может быть принято решение о признании результатов испытаний или утверждении типа СИ, что является основанием для внесения типа импортируемых СИ в Государственный реестр и их применения в РФ. Информация об утверждении типа СИ и решение об его, отмене публикуется в официальных изданиях Госстандарта.
Глава 6. Планирование и проведение физического метрологического эксперимента для построения аналитических моделей объектов и систем. 6.1. Выбор функции отклика и варьируемых параметров.
Задачей эксперимента является получение данных необходимых для установления математической модели (аналитической зависимости), описывающей характеристику устройства или системы, которая в общем виде записывается y = f (x 1, x 2,..., xr), (6.1) где y – выходная характеристика устройства или системы; x 1, x 2,..., xr – входные сигналы и внешние факторы, определяющие поведение устройства или системы. Полученная аналитическая зависимость позволяет предсказывать значения выходной характеристики по значениям входных переменных. Эта возможность важна в случаях, когда прямые измерения выходной характеристики затруднены или дорого стоят. Установление математической модели включает в себя выбор вида математической модели и определение ее параметров (коэффициентов, показателей степени и т.п.). В современной теории эксперимента независимые переменные (x 1, x 2,..., xr) принято называть факторами, а зависимую переменную y – функцией отклика или откликом. Для описания функции отклика могут быть использованы уравнения различного типа, однако при обработке результатов эксперимента часто используют алгебраические полиномы, которые достаточно универсальны и удобны при обработке результатов эксперимента на ЭВМ: y = b 0 + b 1 x 1 + b 2 x 2 + … brxr + … (6.2) В принципе с помощью полиномов можно с высокой степенью точности описать любую гладкую функцию. Для описания сложных процессов обычно используются либо математические модели не выше второго порядка, которые описывают процесс в узком интервале изменения независимых переменных, либо строятся модели для широкого интервала изменения независимых переменных, используя при этом уравнения высоких порядков. В первом из указанных случаев модель оказывается достаточно простой и удобной для применения, но не всегда является достаточно информативной. Во втором случае уравнения содержат значительно больше информации, но их применение затруднительно ввиду большой сложности и громоздкости. Для вычисления параметров моделей высоких порядков требуется большой объем экспериментальных данных. Однако в ряде случаев получение уравнений даже второй степени оказывается невозможным вследствие препятствий математического характера. Наиболее простым является описание процесса с помощью линейной функции. В нелинейном случае сводят, если это возможно к линейному случаю с несколькими независимыми переменными. Например, если f (x) = a + bx + c ln x, то полагая x 1 = x, x 2 = ln x, получаем: f (x) = g (x 1, x 2) = a + bx 1+ c ln x 2. При обработке экспериментальных данных приходится выполнять большой объем вычислений. Для автоматизации вычислений целесообразно использовать один из математических пакетов, функционирующих на ПК. Для решения задач обработки экспериментальных данных популярен интегрированный пакет автоматизации математических вычислений MATLAB фирмы Mathworks (США) [10,11]. Функции, обеспечивающие выполнение простейших процедур анализа данных, включены разработчиками MATLAB в состав ядра системы. Основные инструменты анализа данных сосредоточены в библиотеке Statistics Toolbox (набор инструментов статистического анализа). Всего в библиотеке сосредоточено более 200 функций, обеспечивающих проведение статистических экспериментов, анализ и обработку данных.
6.2. Планирование эксперимента.
Проведение эксперимента на объекте исследования связано с материальными и временными затратами. Поэтому необходимо применение математических методов планирования эксперимента, позволяющих существенно повысить эффективность проведения экспериментальных работ. Применение методов планирования эксперимента предполагает возможность проведения экспериментов в заданных исследователем условиях и выбора в каждом опыте тех уровней факторов, которые представляют интерес. Такой способ проведения эксперимента называют активным. Активный подход к эксперименту в сочетании с методами планирования позволяет получить требуемые результаты, затратив минимальные средства и время на проведение исследования. Каждый фактор имеет область определения. Под областью определения понимается совокупность всех значений, которые в принципе может принимать данный фактор. Совокупность значений фактора, которая используется в эксперименте, является подмножеством из множества значений, образующих область определения. Область определения может непрерывной или дискретной. В реальных задачах планирования эксперимента используются дискретные области определения. Так, для факторов с непрерывной областью определения, таких как, температура, напряжение питания и т.п., всегда выбираются дискретные множества уровней. Под уровнем понимают дискретные значения фактора, которые задаются в процессе эксперимента. К факторам предъявляется ряд требований. Во-первых, факторы должны быть управляемыми. Чтобы точно определить фактор, нужно указать последовательность действий, с помощью которых устанавливаются его конкретные значения. Во-вторых, факторы должны быть однозначны. Трудно управлять фактором, который является функцией других факторов. Кроме того, требования устанавливаются и к совокупности факторов. Прежде всего, факторы должны быть совместимы, т.е. все их комбинации должны быть осуществимы и безопасны. Важна и независимость факторов, т.е. возможность установления фактора на любом уровне вне зависимости от уровней других факторов. При выборе области эксперимента прежде всего необходимо оценить границы областей определения факторов. При этом должны учитываться ограничения нескольких типов. Первый тип – принципиальные ограничения для значений факторов, которые не должны быть нарушены ни при каких обстоятельствах. Например, если фактор – температура, то нижним пределом будет абсолютный нуль. Второй тип – ограничения, связанные с технико-экономическими соображениями, например со стоимостью сырья, дефицитностью отдельных компонентов, временем ведения процесса. Третий тип – ограничения, с которыми чаще всего приходится иметь дело, определяются конкретными условиями проведения процесса, например, существующей аппаратурой, технологией, организацией. Множество всех значений факторов
используемых в эксперименте, где i – номер опыта, представляется с помощью матрицы плана
Выбор числа и значений факторов, обеспечивающих получение наилучших в определенном смысле результатов исследования, составляет цель планирования экспериментов. Процедура выбора подобласти проведения эксперимента включает два этапа: выбор основного уровня и выбор интервалов варьирования. Наилучшим условиям, определенным из анализа априорной информации, соответствует комбинация или несколько комбинаций уровней факторов. Каждая из комбинаций является точкой в факторном пространстве, которую можно рассматриваться как исходную точку для построения плана эксперимента. Назовем ее основным (нулевым) уровнем. Основной уровень x 0 j факторов xj – центр проведения эксперимента. После того, как основной уровень выбран, переходим к следующему шагу – выбору интервалов варьирования. Для каждого фактора необходимо выбрать не менее двух крайних уровня, на которых он будет варьироваться в эксперименте. Представим себе координатную ось, на которой откладывается значение данного фактора, например, температуры. Пусть основной уровень выбран и равен 100°С. Это значение отображается точкой. Тогда два интересующих нас уровня можно отобразить двумя точками, симметричными относительно первой. Один из этих уровней будем называть верхним, а другой нижним. Интервал варьирования фактора Ij – число, прибавление которого к основному уровню дает верхний уровень, а вычитание – нижний уровень варьирования фактора xj. Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбирают так, чтобы верхний уровень соответствовал +1, нижний –1, а основной 0. Для факторов с непрерывной областью определения это всегда можно сделать с помощью преобразования
где Одной из важнейших характеристик плана, влияющей, с одной стороны, на стоимость и длительность исследования, а с другой – на точность результатов, является число экспериментов. План с минимально возможным количеством экспериментов N = r +1(насыщенный план), где r – число оцениваемых параметров модели, не позволяет проверить адекватность модели. Поэтому обычно выбирают N > r +1. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом. Общее число опытов в полном факторном эксперименте (ПФЭ) определяется на основании зависимости N = pr, где N – число опытов, r – число факторов, p – число уровней. Такой эксперимент называется полным факторным, так как в нем полностью использованы все возможные сочетания уровней всех факторов. Для удобства проведения ПФЭ составляется матрица планирования, в которой значению фактора на каждом уровне соответствует условное обозначение кода. Матрица ПФЭ составляется следующим образом: в первом столбце знаки меняются поочередно, во втором – через два, в третьем – через четыре и т.д. по степени двойки. Таблица 1. План эксперимента 22.
Проведение ПФЭ требует больших временных затрат на его подготовку и проведение. Рассмотрим планирование эксперимента для случая 2-х уровней, т.е. p =2. Предположим, что нас интересует функция отклика вида y = b 0 + b 1 x 1+ b 2 x 2. Тогда число оцениваемых параметров r =3, и минимально необходимое число экспериментов для определения параметров модели n = r + 1 = 4. Для этого достаточно провести ПФЭ N = 22 с четырьмя опытами. Однако при этом не останется степеней свободы для проверки адекватности модели. Таким образом, в данном случае двух уровней варьирования факторов не достаточно. При увеличении числа оцениваемых факторов r число опытов N =2 r резко превышает n. Так при r = 6 имеем N = 64, n = 7 и число степеней свободы N – n =57. Очевидно, что в этом случае можно значительно уменьшить число экспериментов. Как правило, ПФЭ проводят при необходимости исследования эффектов взаимодействия всех факторов модели. Для уменьшения объема проводимых опытов используют частичный факторный эксперимент (ЧФЭ). Известны различные способы проведения ЧФЭ. Для определения параметров линейных моделей используются дробные факторные планы, являющиеся подмножествами ПФЭ [6,7]. Разработан ряд критериев оптимальности планов экспериментов [7]. Перечислим некоторые критерии планирования экспериментов, используемые в практических исследованиях. 1. Критерий ортогональности плана. Критерий ортогональности требует выбора такого плана X эксперимента, чтобы матрица (XTX)-1была диагональна. Использование этого критерия имеет целью упрощение вычислений и получение независимых оценок коэффициентов модели. 2. Критерий ротабельности. Этот критерий требует такого расположения точек в области планирования эксперимента, при котором дисперсия оценки значений функции отклика в некоторой точке факторного пространства x зависит только от расстояния этой точки от центра плана. 3. Критерий D-оптимальности. Этот критерий требует такого расположения точек в области планирования эксперимента, при котором определитель матрицы (XTX) максимален. Это приводит к максимальной точности предсказания коэффициентов модели.
Рандомизация. Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой температуры, сырья, лаборанта и т. д.), рекомендуется случайная последовательность при постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать во времени. Термин «рандомизация» происходит от английского слова random – случайный. Рандомизировать во времени означает придать последовательности опытов случайный характер. Приведем простой пример рандомизации условий эксперимента. В полном факторном эксперименте 23 предполагается каждое значение функции отклика определять по двум параллельным опытам. Нужно случайно расположить всего 16 опытов. Присвоим параллельным опытам номера с 9 по 16, и тогда опыт № 9 будет повторным по отношению к первому опыту, десятый – ко второму и т. д. Следующий этап рандомизации – использование таблицы случайных чисел. Обычно таблица случайных чисел приводится в руководствах по математической статистике. В стандартном математическом обеспечении большинства ЭВМ имеются так называемые генераторы случайных чисел.
6.3. Проведение эксперимента на объекте исследования.
Проведению эксперимента предшествует постановка задачи, которая вносится в журнал экспериментатора и включает: · краткое описание объекта; · формулировку цели эксперимента (если задач несколько – ранжирование их по степени важности); · выбор функции отклика; · желаемая точность; · какой результат будет считаться удовлетворительным, какой – неудовлетворительным; · список факторов, которые влияют на объект; · список факторов, включаемых в реальный эксперимент:
Таблица 3.
· заключение о возможности установления значения факторов на любом заданном уровне и сохранения заданных значений уровней в течение опыта; · заключение о невозможности комбинации значений факторов, используемых в эксперименте; · число опытов, ограничения на число опытов; · срок проведения эксперимента; · примерная длительность одного опыта; · стоимость и затраты труда при проведении одного опыта серии; · число уровней для одного фактора; · возможность выполнения параллельных опытов и их число; · возможность проведения параллельных измерений; · стратегия проведения опытов (например, по одному в день и т.п.); · условия и результаты, достигнутые при изучении аналогичных процессов; · результаты предварительного эксперимента и данные (литературные и собственные) о величине ошибки эксперимента; · взаимодействия (взаимовлияние) факторов.
До проведения эксперимента необходимо собрать установку, проверить и прокалибровать измерительные приборы. Журнал заранее оформляют в соответствии с методикой и планом эксперимента, отражая в нем последовательность действий, цели исследования. - Выбирают функцию отклика, с указанием размерности. Описывают все факторы, которые могут служить характеристиками процесса и фиксируют наличие между ними корреляции. Если сведения о корреляции отсутствуют, определяют коэффициенты парной корреляции, проверяют их значимость и выделяют группу некоррелированных факторов. - Формируют таблицу уровней факторов и интервалов варьирования. Указывают единицы измерения факторов. Составляют матрицу планирования. В матрице планирования целесообразно проставлять не только кодовые значения
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.60.62 (0.018 с.) |



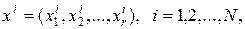
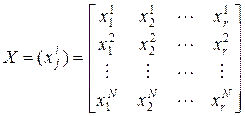 .
.
 – натуральное значение фактора;
– натуральное значение фактора;  – натуральное значение основного уровня; Jj – интервал варьирования; j – номер фактора. Преобразованное значение фактора называют кодированным значением.
– натуральное значение основного уровня; Jj – интервал варьирования; j – номер фактора. Преобразованное значение фактора называют кодированным значением.


