
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 8. Вычисление размерных коэффициентов аналитических моделей объектов и систем по результатам однофакторного эксперимента.Содержание книги
Поиск на нашем сайте
Как уже отмечалось, задачей эксперимента является получение данных необходимых для установления математической модели (аналитической зависимости), описывающей характеристику устройства или системы, которая в общем виде записывается y = f (x 1, x 2,..., xr) + ε, (8.1) где y – выходная характеристика устройства или системы; x 1, x 2,..., xr – входные сигналы и внешние факторы, определяющие поведение устройства или системы, ε – случайная “остаточная” составляющая. Наличие случайной составляющей ε в уравнении (8.1) обусловлено причинами двоякой природы: во-первых, она отражает влияние на формирование значений y факторов, не учтенных в перечне переменных xi; во-вторых, она может включать в себя случайную погрешность в измерении выходной характеристики y. Установление математической модели включает в себя выбор вида математической модели и определение ее параметров (коэффициентов, показателей степени и т.п.). Объективный анализ связи между величинами в значительной степени должен основываться на статистических методах. Для решения задачи построения математической модели системы используется статистический метод обработки наблюдений – метод регрессионного анализа. В схеме регрессионного анализа предполагается, что независимые переменные (факторы) xi являются неслучайными величинами, значения которых задаются заранее, перед началом эксперимента; зависимая переменная y – случайная величина. Нас интересует только среднее значение y при заданных xi –
Предполагается, что математическое ожидание, от случайной составляющей ε в уравнении (8.1) равно нулю: M [ε] = 0. В регрессионном анализе вид функции предполагается известным и по результатам эксперимента нужно значения неизвестных коэффициентов модели b 0, b 1, b 2,… При выборе вида кривой регрессии следует использовать экспертные оценки, т.е. совокупность сведений профессионального характера об изучаемом реальном устройстве или системе. Обоснованное применение регрессионного анализа требует выполнения ряда предпосылок: 1) при каждых значениях xi, 2) дисперсия D [ y (x)] величины y постоянна: D [ y (x)] = σ2, где σ = const. 3) наблюдения являются стохастически независимыми. 4) факторы не должны быть линейно связаны с другими независимыми переменными. Замечание. Третье условие регрессионного анализа часто нарушается при использовании времени в качестве одного из факторов. Существует много разнообразных методов обработки результатов эксперимента. Обоснованный и точный выбор метода для оценки параметров математической модели опирается на знание вероятностной природы (типа закона распределения) остатков ε в модели (8.1). Если при любых значениях xi, Рассмотрим применение метода наименьших квадратов для определения коэффициентов b 0 и b 1 линейной функции отклика с одним фактором вида y = b 0 + b 1 x. (8.2) Если бы все экспериментальные точки лежали строго на прямой линии, то для каждой из них было бы справедливо равенство y i – b 0 – b 1 x i = 0, (8.3) где i = 1, 2,..., n – номер опыта. На практике это неравенство нарушается и вместо него используется: y i – b 0 – b 1 x i = xi, (8.4) где xi – разность между экспериментальным и вычисленным по уравнению регрессии значениями y в i -ой экспериментальной точке, эту величину называют невязкой. Необходимо найти такие коэффициенты регрессии, при которых невязки будут минимальны. Выражение минимизации невязки
приводит к методу наименьших квадратов (МНК). Уравнение регрессии содержит два неизвестных коэффициента. Значит, применяя МНК, получим два уравнения. Соотношение (8.5) запишем в следующем виде:
Минимум функции достигается при одновременном равенстве нулю частных производных по всем неизвестным:
Из соотношения (8.6) с учетом (8.7) получаем уравнения для определения коэффициентов функции отклика
если раскрыть скобки, то получим
Окончательно формулы для вычисления коэффициентов регрессии имеют вид
График аппроксимирующего линейного полинома представлен на рис.2. Экспериментально полученные результатам обозначены кружками.
Рис. 2.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.170.196 (0.007 с.) |

 , т.е. функциональная зависимость условного среднего значения функции отклика y (при условии, что факторы xi,
, т.е. функциональная зависимость условного среднего значения функции отклика y (при условии, что факторы xi,  , фиксированы) от xi:
, фиксированы) от xi: = f (x 1, x 2,..., xr, b 0, b 1, b 2, …).
= f (x 1, x 2,..., xr, b 0, b 1, b 2, …).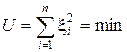 (8.5)
(8.5)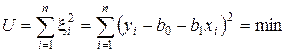 (8.6)
(8.6)
 (8.7)
(8.7) (8.8)
(8.8)
 (8.9)
(8.9)
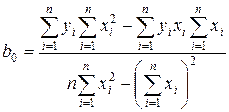 , (8.10)
, (8.10) .
.



