Глава 4. Характеристики средств измерений

 

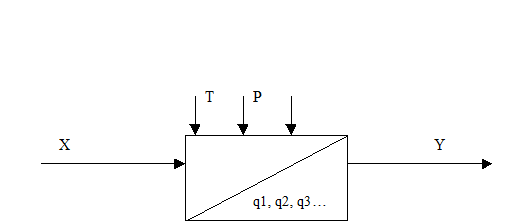
В общем случае измерительное устройство (рис.5), преобразует входную физическую величину Х в выходную Y, при этом, на результат измерения влияют внешние факторы, например, температура Т и давления Р окружающей среды и т.д., а также вариация внутренних параметров: q1, q2, q3 …, которые являются источниками погрешности измерительного устройства.

 

 

 

Рис.5

 

Метрологические характеристики это устанавливаемые нормативной документацией количественные характеристики, определяющие точность и область применения средств измерений.

К основным метрологическим характеристикам относятся.

Диапазон измерений – область значений величи­ны, в пределах которых нормированы допускаемые пределы погрешности. Значения величины, ограни­чивающие диапазон измерений снизу или сверху (слева и справа), называют соответственно нижним или верхним пределом измерений.

Порог чувствительности – наименьшее измене­ние измеряемой величины, которое вызывает заметное изменение выходного сигнала. Например, если порог чувствительности весов равен 10 мг, то это озна­чает, что заметное перемещение стрелки весов достигается при таком малом изменении массы, как 10 мг.

Погрешность – это разность между показаниями СИ и истинным значением измеряемой физической величины. Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением. Для СИ за действительное значение принимают показания рабочего эталона.

D X _n = X _n – X ₀, (4.1)

D X _n – погрешность поверяемого СИ; X _n – значение физической величины, найденное с помощью поверяемого СИ; X ₀ – значение физической величины, принятое за базу для сравнения – действительное значение (показания рабочего эталона). Например, при измерении барометром атмосферного давления получено значение X _n = 1017 гПа. За действительное значение принято показание рабочего эталона, которое равнялось X ₀ = 1020 гПа. Следо­вательно, погрешность измерения барометром составила:

D X _n = 1017 - 1020 = –3 гПа. (4.2)

Погрешности СИ классифицируются по ряду признаков, в частности:

· по способу выражения – абсолютные, относительные;

· по характеру проявления – систематические, случайные;

· по отношению к условиям применения – основные, дополнительные.

Абсолютная погрешность D X _n является разностью между показаниями СИ и истинным (действительным) значением измеряемой физической величины, выраженной в единицах измерения измеряемой физической величины, определяется по формуле (4.1).

Относительная погреш­ность (d) - отношение абсолютной погрешности к действительному значению измеряемой величины, выраженное в процентах:

d = 100·D X _n / X ₀ (4.3).

Точность - величина обратная относительной погрешности – 1/d. Если погрешность d = 0,1% или 10^-3, то точность, равна 10³.

Систематическая погрешность – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины в одинаковых условиях.

Систематическую погрешность устраняют введением поправок.

Случайная погрешность – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины в одинаковых условиях.

Случайная погрешность всегда присутствует в результатах измерения и порождает рассеяние результатов измерения.

Характеристиками рассеяния результатов измерений, одной и той же величины, вследствие влияния случайных погрешностей, являются дисперсия или среднее квадратичное отклонение (S _d).

Обычно метрологические характеристики СИ нормируют раздельно для нормальных и рабочих условий эксплуатации.

Основная погрешность СИ – погрешность, определяемая при нормальных условиях эксплуатации СИ.

Дополнительная погрешность СИ – составляющая погрешности СИ, дополнительно возникающая, вследствие отклонения рабочих условий эксплуатации СИ от нормальных.

Под нормальными условиями эксплуатации, как правило, принимают условия с температурой окружающей среды (298 ± 15) К, атмосферным давлением 760 мм.рт.ст., относительной влажностью (65 ± 15)%, параметрами электропитания в сети соответствующим номинальным, положением СИ в пространстве соответствующим стандартному и т.д. Дополнительная погрешность СИ суммируется с основной и нормируется через коэффициенты и функции влияния внешних факторов и внутренних параметров СИ на погрешность.

Сходимость результатов измерений – характеристика, отражающая близость друг к другу результатов измерении одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях.

Количественная оценка сходимости может быть дана с помощью разных показателей, например, разности среднего арифметического двух параллельных измерений.

Воспроизводимость результатов измерений – повторяемость результатов измерений одной и той же величины, полученных в разных местах, разными ме­тодами, в разное время, но приведенных к одним и тем же условиям измерений (тем­пературе, давлению, влажности и др.).

Номенклатура и предельные значения нормируемых метрологических характеристик СИ определяются техническими условиями (ТУ) на СИ и зависят от назначения, условий эксплуатации и других факторов.

Класс точности СИ – предельно допустимое суммарное значение основной и дополнительной погрешностей.

Как правило, класс точности обозначают числовым значением, которое равно предельно допустимому суммарному значению основной и дополнительной погрешностей, выраженному в процентах. Так, класс точности 0,001 свидетельствует о том, что суммарное значение основной и дополнительной погрешностей СИ не превышает 0,001%.

Уравнение измерения - математическое описание (математическая модель) процедуры сравнения неизвестного размера Q физической величины с единицой измерения [ Q ]. Уравнение измерения имеет вид:

 

Q /[ Q ] = Х.

 

В качестве единицы измерения [ Q ] при измерении физических величин выступает соответствующая единица измерения Международной системы единиц или внесистемная единица. Значение единицы измерения заложено в память СИ при его градуировке, например при разметке шкалы, или указывается в технической документации на СИ.

Теоретически отношение двух размеров физических величин должно быть вполне определенным, неслучайным числом. На практике при проведении измерений размеры физических величин сравниваются в условиях множества случайных обстоятельств. Поэтому при многократном измерении одной и той же величины по­стоянного размера результат измерения является случайным числом.

При подготовке и проведении высокоточных измерений в метрологической практике учитывают влияние объекта измерения, метода измерения, средства измерения, условий измерения, экспериментатора (оператора). Оператор, вносит в результат из­мерения промахи и погрешности, которые зависят от квалификации, санитарно-гигиенических и эргономических условий труда, психофизиологического состояния оператора.

Часто измерение одной и той же величины постоянного размера разными мето­дами дает различные результаты, причем каждый из них имеет свои недостатки и достоинства. Искусство оператора состоит в том, чтобы соответствующими способами исключить, компенсировать или учесть факторы, искажающие результаты. Если измерение не удается выполнить так, чтобы исключить или компенсировать какой-либо фактор, влияющий на результат, то в последний вносят поправку.

Поправки могут быть аддитивными (от лат. additivus – прибавляемый) и мультипликативными (от лат. multipico – умножаю). Например, для расчета сопротивления измеряют значение электрического тока, протекающего через резистор, и падение напряжения на нем. При этом возможны два варианта включения вольтметра и амперметра и соответственно различные аддитивные поправки. В одном случае из показания амперметра нужно вычесть ток, протекающий через вольтметр, в другом – из показания у вольтметра нужно вычесть, падение напряжения на амперметре. Другой пример (по учету мультипликативной поправки): при измерении ЭДС вольтметром учитывают сопротивление источника питания путем умножения показания вольтметра на поправочный множитель, определяемый расчетным путем.

Влияние СИ на измеряемую величину во многих случаях проявляется как возмущающий фактор. Например, ртутный термометр, опущенный в пробирку с охлажденной жидкостью, подогревает ее и показывает не первоначальную температуру жидкости, а температуру, при которой устанавливается термодинамическое равновесие. Другим фактором является инерционность СИ.

По итогам устанавливается аддитивная, или мультипликативная поправка в виде числа или функции, она может задаваться графиком, таблицей или формулой.

Условия измерения как влияющий на результат фактор включают температуру; окружающей среды, влажность, атмосферное давление, напряжение в сети и многое другое.

Рассмотрев факторы, влияющие на результаты измерений, можно сделать следующие выводы: при подготовке к измерениям они должны по возможности исключаться, в процессе измерения компенсиро­ваться, а после измерения учитываться.

Учет указанных факторов предполагает исключение ошибок и внесение поправок к измеренным величинам.

Появление ошибок вызвано недостаточной надежностью системы, в которую входят оператор, объ­ект измерения, СИ и окружающая среда. В данной системе могут происходить отказы аппаратуры, отвлечение внимания человека, описки в записях сбои в аппаратуре, колебания напряжения в сети.

При однократном измерении ошибка может быть выявлена при сопоставлении результата с априорным, представлением о нем или путем логического анализа. Измерения повторяют для устранения причины ошибки.

При многократном измерении одной и той же величины ошибки проявляются в том, что результаты отдельных измерений заметно отличаются от остальных. Если отличие велико, ошибочный результат необходимо отбросить. При этом руководствуются «правилом трех сигм»: если при многократном измерений сомнительный результат отдельного измере­ния отличается от среднего больше чем на 3δ (δ –среднее квадратическое отклонение значения измеряемой величины от среднего значения); то с вероятностью 0,997 он является ошибочным и его следует отбросить. Условно к однократному измерению относят двукратные и трехкратные измерения, так как для большей уверенности в получаемом результате одним измерением не ограничиваются. Начиная с какого числа можно считать измерение многократным? Практически при четырем измерениях, и более измерение, можно считать многократным, так как именно при этом минимальном числе отдельных измерений может быть произведена математическая обработка.

Качество измерений является главным фактором производства, базирующегося на быстропротекающих процессах, автоматических процессах на боль­шом числе измеряемых величин. Нередко причиной брака продукции становятся неверно назначенные СИ (в первую очередь по точности). Бывает и так, что СИ вовсе не назначаются там, где это необходимо, из-за: их отсутствия. Как доказывает анализ, если весь брак, причиной которого являются недостатки метрологической деятельности, принять за 100%, брак продукции вследствие неправильно выбранных или совсем не назначенных СИ составит 48,5%; из-за неумелого применения СИ, отсутствия метрологически аттестованных методик измерения и низкой квалификации операторов - 46%; 5,5% обуславливается неисправностьюСИ.