
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Государственная система обеспечения единства измеренийСодержание книги
Поиск на нашем сайте
Единство измерений – состояние системы измерений, при котором достигаются сопоставимые по точности результаты измерений одних и тех величин, выполненных в разное время, в разных местах, с помощью разных методов и технических средств. Задача единства измерений решается метрологическими службами, которые обеспечивают выполнение государственных стандартов и других нормативных документов в области метрологии. Государственный метрологический контроль и надзор осуществляют Государственная метрологическая служба РФ (ГМС), метрологические службы федеральных органов исполнительной власти, метрологические службы юридических лиц, международные метрологические организации. Государственная метрологическая служба находится в ведении Госстандарта РФ и включает: Государственные научные метрологические центры (ГНМЦ), органы Государственной метрологической службы РФ в субъектах РФ. Государственными научными метрологическими центрами являются: ВНИИ метрологической службы (ВНИИМС, г. Москва), ВНИИ метрологии им. Д.И. Менделеева (ВНИИМ, г. Санкт-Петербург); НПО «ВНИИ физико-технических и радиотехнических измерений» (ВНИИФТРИ, пос. Менделеево, Московской обл.); Уральский НИИ метрологии (УНИИМ, г. Екатеринбург) и др. Государственные научные метрологические центры разрабатывают научно-методические основы совершенствования российской системы измерений и являются держателями государственных эталонов. Функции региональных органов Государственной метрологической службы РФ в субъектах РФ выполняют более 100 центров стандартизации и метрологии. В систему Госстандарта входят государственные справочные службы: Государственная служба времени, частоты и определения параметров вращения Земли, Государственная служба стандартных образцов состава и свойств веществ и материалов и Государственная служба стандартных справочных данных о физических константах и свойствах веществ и материалов. Ведущей международной метрологической организацией является Международное бюро мер и весов, которое координирует деятельность метрологических организаций более чем 100 стран мира. Международное бюро мер и весов хранит международные прототипы метра и килограмма и некоторые другие эталоны, а также организует периодическое сличение национальных эталонов с международными, располагается во Франции, в г. Севр. Руководство деятельностью Международного бюро мер и весов осуществляет Международным комитетом мер и весов.
С 1956 г. действует Международная организация законодательной метрологии, членами которой являются более 80 стран мира. Усилиями международных метрологических организаций на сегодня в 51 стране мира принята Международная система единиц физических величин, действует сопоставимая терминология, приняты рекомендации по способам нормирования метрологических характеристик СИ, по сертификации СИ, по испытаниям СИ перед выпуском серийной продукции. Нормативная база метрологии
Комплекс нормативных документов, устанавливающих правила, нормы, требования, направленные на достижение и поддержание единства измерений в стране при требуемой точности, составляет государственную систему обеспечения единства измерений. К системе относятся: Федеральный закон Российской Федерации от 26 июня 2008 г. N 102-ФЗ "Об обеспечении единства измерений". Государственные стандарты (ГОСТ, ГОСТ Р) системы обеспечения единства измерений. Правила государственной системы обеспечения единства измерений, утверждаемые Госстандартом РФ. Рекомендации (гриф «МИ») государственной системы обеспечения единства измерений, разрабатываемые государственными метрологическими научными центрами.
Процедуру соблюдения правил законодательной метрологии обеспечивает комплекс нормативных документов, которые регламентирует государственный метрологический контроль за: утверждением типа средств измерений, поверкой средств измерений, в том числе эталонов, лицензированием деятельности юридических и физических лиц по изготовлению, ремонту, продаже и прокату средств измерений. Процедуру утверждения типа проводят для новых СИ, предназначенных для производства или ввоза по импорту. Процедура предусматривает обязательные испытания СИ на соответствие, государственную регистрацию, выдачу сертификата об утверждении типа. Испытания проводятся государственными научными метрологическими центрами, аккредитованными в качестве государственных центров испытаний СИ (ГЦИ СИ). Утвержденный тип СИ вносится в Государственный реестр, который ведет Госстандарт. На СИ утвержденного типа и эксплуатационные документы, сопровождающие каждый экземпляр, наносится знак утверждения типа установленной формы (рис. 8). Знаки в метрологии: а – знак утверждения типа, б – поверительное клеймо, в – знак системы добровольной сертификации.
Рис.8
Каждый экземпляр СИ при выпуске из производства или ремонта, при ввозе по импорту подлежит поверке органами государственного метрологического контроля. В соответствии с международными соглашениями, заключенными Россией с другими странами, Госстандартом может быть принято решение о признании результатов испытаний или утверждении типа СИ, что является основанием для внесения типа импортируемых СИ в Государственный реестр и их применения в РФ. Информация об утверждении типа СИ и решение об его, отмене публикуется в официальных изданиях Госстандарта.
Глава 6. Планирование и проведение физического метрологического эксперимента для построения аналитических моделей объектов и систем. 6.1. Выбор функции отклика и варьируемых параметров.
Задачей эксперимента является получение данных необходимых для установления математической модели (аналитической зависимости), описывающей характеристику устройства или системы, которая в общем виде записывается y = f (x 1, x 2,..., xr), (6.1) где y – выходная характеристика устройства или системы; x 1, x 2,..., xr – входные сигналы и внешние факторы, определяющие поведение устройства или системы. Полученная аналитическая зависимость позволяет предсказывать значения выходной характеристики по значениям входных переменных. Эта возможность важна в случаях, когда прямые измерения выходной характеристики затруднены или дорого стоят. Установление математической модели включает в себя выбор вида математической модели и определение ее параметров (коэффициентов, показателей степени и т.п.). В современной теории эксперимента независимые переменные (x 1, x 2,..., xr) принято называть факторами, а зависимую переменную y – функцией отклика или откликом. Для описания функции отклика могут быть использованы уравнения различного типа, однако при обработке результатов эксперимента часто используют алгебраические полиномы, которые достаточно универсальны и удобны при обработке результатов эксперимента на ЭВМ: y = b 0 + b 1 x 1 + b 2 x 2 + … brxr + … (6.2) В принципе с помощью полиномов можно с высокой степенью точности описать любую гладкую функцию. Для описания сложных процессов обычно используются либо математические модели не выше второго порядка, которые описывают процесс в узком интервале изменения независимых переменных, либо строятся модели для широкого интервала изменения независимых переменных, используя при этом уравнения высоких порядков. В первом из указанных случаев модель оказывается достаточно простой и удобной для применения, но не всегда является достаточно информативной. Во втором случае уравнения содержат значительно больше информации, но их применение затруднительно ввиду большой сложности и громоздкости. Для вычисления параметров моделей высоких порядков требуется большой объем экспериментальных данных. Однако в ряде случаев получение уравнений даже второй степени оказывается невозможным вследствие препятствий математического характера.
Наиболее простым является описание процесса с помощью линейной функции. В нелинейном случае сводят, если это возможно к линейному случаю с несколькими независимыми переменными. Например, если f (x) = a + bx + c ln x, то полагая x 1 = x, x 2 = ln x, получаем: f (x) = g (x 1, x 2) = a + bx 1+ c ln x 2. При обработке экспериментальных данных приходится выполнять большой объем вычислений. Для автоматизации вычислений целесообразно использовать один из математических пакетов, функционирующих на ПК. Для решения задач обработки экспериментальных данных популярен интегрированный пакет автоматизации математических вычислений MATLAB фирмы Mathworks (США) [10,11]. Функции, обеспечивающие выполнение простейших процедур анализа данных, включены разработчиками MATLAB в состав ядра системы. Основные инструменты анализа данных сосредоточены в библиотеке Statistics Toolbox (набор инструментов статистического анализа). Всего в библиотеке сосредоточено более 200 функций, обеспечивающих проведение статистических экспериментов, анализ и обработку данных.
6.2. Планирование эксперимента.
Проведение эксперимента на объекте исследования связано с материальными и временными затратами. Поэтому необходимо применение математических методов планирования эксперимента, позволяющих существенно повысить эффективность проведения экспериментальных работ. Применение методов планирования эксперимента предполагает возможность проведения экспериментов в заданных исследователем условиях и выбора в каждом опыте тех уровней факторов, которые представляют интерес. Такой способ проведения эксперимента называют активным. Активный подход к эксперименту в сочетании с методами планирования позволяет получить требуемые результаты, затратив минимальные средства и время на проведение исследования. Каждый фактор имеет область определения. Под областью определения понимается совокупность всех значений, которые в принципе может принимать данный фактор. Совокупность значений фактора, которая используется в эксперименте, является подмножеством из множества значений, образующих область определения. Область определения может непрерывной или дискретной. В реальных задачах планирования эксперимента используются дискретные области определения. Так, для факторов с непрерывной областью определения, таких как, температура, напряжение питания и т.п., всегда выбираются дискретные множества уровней. Под уровнем понимают дискретные значения фактора, которые задаются в процессе эксперимента.
К факторам предъявляется ряд требований. Во-первых, факторы должны быть управляемыми. Чтобы точно определить фактор, нужно указать последовательность действий, с помощью которых устанавливаются его конкретные значения. Во-вторых, факторы должны быть однозначны. Трудно управлять фактором, который является функцией других факторов. Кроме того, требования устанавливаются и к совокупности факторов. Прежде всего, факторы должны быть совместимы, т.е. все их комбинации должны быть осуществимы и безопасны. Важна и независимость факторов, т.е. возможность установления фактора на любом уровне вне зависимости от уровней других факторов. При выборе области эксперимента прежде всего необходимо оценить границы областей определения факторов. При этом должны учитываться ограничения нескольких типов. Первый тип – принципиальные ограничения для значений факторов, которые не должны быть нарушены ни при каких обстоятельствах. Например, если фактор – температура, то нижним пределом будет абсолютный нуль. Второй тип – ограничения, связанные с технико-экономическими соображениями, например со стоимостью сырья, дефицитностью отдельных компонентов, временем ведения процесса. Третий тип – ограничения, с которыми чаще всего приходится иметь дело, определяются конкретными условиями проведения процесса, например, существующей аппаратурой, технологией, организацией. Множество всех значений факторов
используемых в эксперименте, где i – номер опыта, представляется с помощью матрицы плана
Выбор числа и значений факторов, обеспечивающих получение наилучших в определенном смысле результатов исследования, составляет цель планирования экспериментов. Процедура выбора подобласти проведения эксперимента включает два этапа: выбор основного уровня и выбор интервалов варьирования. Наилучшим условиям, определенным из анализа априорной информации, соответствует комбинация или несколько комбинаций уровней факторов. Каждая из комбинаций является точкой в факторном пространстве, которую можно рассматриваться как исходную точку для построения плана эксперимента. Назовем ее основным (нулевым) уровнем. Основной уровень x 0 j факторов xj – центр проведения эксперимента. После того, как основной уровень выбран, переходим к следующему шагу – выбору интервалов варьирования. Для каждого фактора необходимо выбрать не менее двух крайних уровня, на которых он будет варьироваться в эксперименте. Представим себе координатную ось, на которой откладывается значение данного фактора, например, температуры. Пусть основной уровень выбран и равен 100°С. Это значение отображается точкой. Тогда два интересующих нас уровня можно отобразить двумя точками, симметричными относительно первой. Один из этих уровней будем называть верхним, а другой нижним. Интервал варьирования фактора Ij – число, прибавление которого к основному уровню дает верхний уровень, а вычитание – нижний уровень варьирования фактора xj.
Для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбирают так, чтобы верхний уровень соответствовал +1, нижний –1, а основной 0. Для факторов с непрерывной областью определения это всегда можно сделать с помощью преобразования
где Одной из важнейших характеристик плана, влияющей, с одной стороны, на стоимость и длительность исследования, а с другой – на точность результатов, является число экспериментов. План с минимально возможным количеством экспериментов N = r +1(насыщенный план), где r – число оцениваемых параметров модели, не позволяет проверить адекватность модели. Поэтому обычно выбирают N > r +1. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом. Общее число опытов в полном факторном эксперименте (ПФЭ) определяется на основании зависимости N = pr, где N – число опытов, r – число факторов, p – число уровней. Такой эксперимент называется полным факторным, так как в нем полностью использованы все возможные сочетания уровней всех факторов. Для удобства проведения ПФЭ составляется матрица планирования, в которой значению фактора на каждом уровне соответствует условное обозначение кода. Матрица ПФЭ составляется следующим образом: в первом столбце знаки меняются поочередно, во втором – через два, в третьем – через четыре и т.д. по степени двойки. Таблица 1. План эксперимента 22.
Проведение ПФЭ требует больших временных затрат на его подготовку и проведение. Рассмотрим планирование эксперимента для случая 2-х уровней, т.е. p =2. Предположим, что нас интересует функция отклика вида y = b 0 + b 1 x 1+ b 2 x 2. Тогда число оцениваемых параметров r =3, и минимально необходимое число экспериментов для определения параметров модели n = r + 1 = 4. Для этого достаточно провести ПФЭ N = 22 с четырьмя опытами. Однако при этом не останется степеней свободы для проверки адекватности модели. Таким образом, в данном случае двух уровней варьирования факторов не достаточно. При увеличении числа оцениваемых факторов r число опытов N =2 r резко превышает n. Так при r = 6 имеем N = 64, n = 7 и число степеней свободы N – n =57. Очевидно, что в этом случае можно значительно уменьшить число экспериментов. Как правило, ПФЭ проводят при необходимости исследования эффектов взаимодействия всех факторов модели. Для уменьшения объема проводимых опытов используют частичный факторный эксперимент (ЧФЭ). Известны различные способы проведения ЧФЭ. Для определения параметров линейных моделей используются дробные факторные планы, являющиеся подмножествами ПФЭ [6,7]. Разработан ряд критериев оптимальности планов экспериментов [7]. Перечислим некоторые критерии планирования экспериментов, используемые в практических исследованиях. 1. Критерий ортогональности плана. Критерий ортогональности требует выбора такого плана X эксперимента, чтобы матрица (XTX)-1была диагональна. Использование этого критерия имеет целью упрощение вычислений и получение независимых оценок коэффициентов модели. 2. Критерий ротабельности. Этот критерий требует такого расположения точек в области планирования эксперимента, при котором дисперсия оценки значений функции отклика в некоторой точке факторного пространства x зависит только от расстояния этой точки от центра плана. 3. Критерий D-оптимальности. Этот критерий требует такого расположения точек в области планирования эксперимента, при котором определитель матрицы (XTX) максимален. Это приводит к максимальной точности предсказания коэффициентов модели.
Рандомизация. Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой температуры, сырья, лаборанта и т. д.), рекомендуется случайная последовательность при постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать во времени. Термин «рандомизация» происходит от английского слова random – случайный. Рандомизировать во времени означает придать последовательности опытов случайный характер. Приведем простой пример рандомизации условий эксперимента. В полном факторном эксперименте 23 предполагается каждое значение функции отклика определять по двум параллельным опытам. Нужно случайно расположить всего 16 опытов. Присвоим параллельным опытам номера с 9 по 16, и тогда опыт № 9 будет повторным по отношению к первому опыту, десятый – ко второму и т. д. Следующий этап рандомизации – использование таблицы случайных чисел. Обычно таблица случайных чисел приводится в руководствах по математической статистике. В стандартном математическом обеспечении большинства ЭВМ имеются так называемые генераторы случайных чисел.
6.3. Проведение эксперимента на объекте исследования.
Проведению эксперимента предшествует постановка задачи, которая вносится в журнал экспериментатора и включает: · краткое описание объекта; · формулировку цели эксперимента (если задач несколько – ранжирование их по степени важности); · выбор функции отклика; · желаемая точность; · какой результат будет считаться удовлетворительным, какой – неудовлетворительным; · список факторов, которые влияют на объект; · список факторов, включаемых в реальный эксперимент:
Таблица 3.
· заключение о возможности установления значения факторов на любом заданном уровне и сохранения заданных значений уровней в течение опыта; · заключение о невозможности комбинации значений факторов, используемых в эксперименте; · число опытов, ограничения на число опытов; · срок проведения эксперимента; · примерная длительность одного опыта; · стоимость и затраты труда при проведении одного опыта серии; · число уровней для одного фактора; · возможность выполнения параллельных опытов и их число; · возможность проведения параллельных измерений; · стратегия проведения опытов (например, по одному в день и т.п.); · условия и результаты, достигнутые при изучении аналогичных процессов; · результаты предварительного эксперимента и данные (литературные и собственные) о величине ошибки эксперимента; · взаимодействия (взаимовлияние) факторов.
До проведения эксперимента необходимо собрать установку, проверить и прокалибровать измерительные приборы. Журнал заранее оформляют в соответствии с методикой и планом эксперимента, отражая в нем последовательность действий, цели исследования. - Выбирают функцию отклика, с указанием размерности. Описывают все факторы, которые могут служить характеристиками процесса и фиксируют наличие между ними корреляции. Если сведения о корреляции отсутствуют, определяют коэффициенты парной корреляции, проверяют их значимость и выделяют группу некоррелированных факторов. - Формируют таблицу уровней факторов и интервалов варьирования. Указывают единицы измерения факторов. Составляют матрицу планирования. В матрице планирования целесообразно проставлять не только кодовые значения факторов, но и натуральные. В журнал заносят даты проведения эксперимента, фамилии экспериментатора. Результаты анализа эксперимента и расчеты.
6.4. Основные этапы подготовки и проведения эксперимента.
Покажем на примере основные этапы подготовки и проведения эксперимента. 1. Цель исследования. Определить аналитическую зависимость между выходным параметром экспериментальной установки и факторами, определяющими процесс. 2. Параметры, характеризующие процесс: y 1 – выходной параметр, у 2 – ограничение. 3. Факторы, определяющие процесс (варьируемые факторы): x 1 – измеряемая величина; x 2 – температура среды, °С; x 3 – давление, Па.
4. Формулировка задачи. Получить сведения о влиянии фактора х 1, x 2, x 3 на выходной параметр y 1, при ограничении у 2. 5. Варьируемые факторы. Принято решение изменять в опытах факторы x 1, x 2 и x 3. 6. Описание экспериментальной установки. Приводится техническое описание установки. 7. Опубликованные данные и сведения из отчетов других исследователей (априорная информация), влияние факторов. 8. На основании анализа имеющихся сведений выбираются уровни и интервалы варьирования факторов. Пример таблицы кодирования уровней эксперимента для трех факторов варьируемых на трех уровнях, 10%, 50%, 90% от диапазона изменения значений факторов.
Таблица 4.
9. Проведение эксперимента с занесением его результатов в таблицу планирования и результатов эксперимента.
Таблица 5. Пример таблицы планирования и результаты эксперимента
Имея такую таблицу, можно приступить к обработке экспериментальных данных.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.183.165 (0.017 с.) |


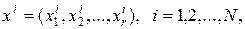
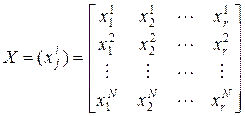 .
.
 – натуральное значение фактора;
– натуральное значение фактора;  – натуральное значение основного уровня; Jj – интервал варьирования; j – номер фактора. Преобразованное значение фактора называют кодированным значением.
– натуральное значение основного уровня; Jj – интервал варьирования; j – номер фактора. Преобразованное значение фактора называют кодированным значением.


