
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электронно-лучевой осциллографСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
СОДЕРЖАНИЕ ВВЕДЕНИЕ.. 5 ЛАБОРАТОРНА РОБОТА №1 ОСЦИЛЛОГРАФИЧЕСКИЕ ИЗМЕРЕНИЯ.. 6 ЛАБОРАТОРНА РОБОТА №2 ИЗМЕРЕНИЕ ПОСТОЯННОГО НАПРЯЖЕНИЯ И СИЛЫ ЭЛЕКТРИЧЕСКОГО ТОКА.. 31 ЛАБОРАТОРНА РОБОТА №3 ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ПРЯМЫМ И КОСВЕННЫМ МЕТОДАМИ.. 47 ЛАБОРАТОРНА РОБОТА №4 ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОКРАТНЫХ РАВНОТОЧНЫХ НАБЛЮДЕНИЙ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ.. 51 СПИСОК ЛИТЕРАТУРЫ... 70
ВВЕДЕНИЕ В методических указаниях описан цикл лабораторных работ, которые выполняются студентами (в том числе иностранными студентами) факультета электроники в соответствии с учебным планом дисциплины «Ведение к технике измерений», который входит в вариативную часть программы подготовки бакалавров. Описанные лабораторные работы включают: измерение напряжения, тока (постоянного и переменного) и сопротивления аналоговыми и цифровыми электронными приборами; проведение осциллографических измерений периодических гармонических и импульсных сигналов, обработку многократных равноточных измерений. Описания лабораторных работ содержат основные теоретические сведения о явлениях и процессах, которые исследуются, методики эксперимента и рабочие задания, контрольные вопросы и рекомендованную литературу. Для успешного выполнения лабораторных работ студенту необходимо познакомиться с их целью и объектом исследования. Кроме того, выполнение работы возможно только после освоения метода исследования, ознакомлением с конструкцией лабораторного макета и измерительными приборами. Заключительным этапом работы является итоговый отчет, в котором самая важная творческая часть – выводы по результатам измерений. ЛАБОРАТОРНА РОБОТА №1 Цель работы: изучить работу электронно-лучевого осциллографа; научиться получать осциллограммы и измерять параметры периодических сигналов Измерение параметров гармонического сигнала Параметры гармонического сигнала (рис. 1.13): - амплитуда Um – наибольшее из мгновенных значений напряжения за период повторения Т; - период повторения Т – интервал времени от одного мгновенного значения до следующего мгновенного значения того же уровня при том же значении производной dU(t)/dt; -
частота повторения f – количество периодов колебаний за 1с,  . .
Рисунок 1.13 – Гармонический сигнал Генератор гармонических сигналов ГЗ-109 При включении вырабатывает переменное напряжение в соответствии с установленной оператором частотой от 20 Гц до 200кГц. Амплитуда выходного сигнала может регулироваться оператором и измеряется встроенным вольтметром. Измерение параметров периодического прямоугольного импульсного сигнала Параметры периодического импульсного сигнала: - амплитуда Uт – наибольшее из мгновенных значений (за период повторения Т); - период повторения Т – временной интервал от любого мгновенного значения сигнала до следующего мгновенного значения сигнала того же уровня (при одном значении производной); - частота повторения f – количество периодов колебаний за 1с; - длительность импульса t и – временной интервал на уровне 0.5 Um; - передний фронт - задний фронт (срез) Иногда длительность импульса указывают на некотором заданном уровне, например, на уровне 0,1 Um – Импульсный сигнал считают прямоугольным, если длительность плоской части на уровне Um составляет более трех длительностей На рис. 1.14 изображен периодически повторяющийся импульсный сигнал положительной полярности.
Рисунок 1.14 – Параметры периодического импульсного сигнала Выполнение лабораторной работы Подготовка осциллографа к измерениям – калибровка. Измерение параметров калибровочного сигнала Состав оборудования: осциллограф, кабель. Включить осциллограф переключателем «Сеть», поставить переключатель синхронизации П2 в положение «Внутр» или «Сеть». Вращая регулировку «Уровень», получить изображение линии развертки. Регулировкой «Смещение Y» установить линию в центре экрана, регулировкой «Смещение X» совместить начало развертки с крайним левым делением шкалы. Регулировками «Яркость» и «Фокус» установить необходимую яркость и четкость изображения линии. Включить калибратор, поставить положение переключателя П2 в положение «Внутр. синхр.», переключатель П4 в положение «+», переключатель «Вольт/дел.» поставить в такое положение, чтобы изображение сигнала меры по вертикали занимало всю шкалу, а переключатель «Время/ дел.» в положение, при котором на экране виден период колебания сигнала калибратора. Регулируя «Уровень» и «Стабильность», получить осциллограмму (рис. 16). Измерить параметры калибровочного сигнала.
Сигнал калибратора имеет параметры: U м = 100 мВ, f м = 2 кГц. Определяем: ТМ = 0,5·10-3 с = 500 мкс
Рисунок 1.16 – Осциллограмма калибровочного сигнала По результатам измерений рассчитываем:
Если измеренные значения UМ изм, TМ изм не соответствуют параметрам сигнала меры, то, вращая «верхние части» переключателей «Вольт/дел.» и «Время/дел.», установить их в такие положения, при котором измеренные значения UМ изм и TМ изм будут равны известным параметрам (UМ, TМ) сигнала меры. При калибровке переключатели П1 и ПЗ могут находиться в любом положении, так как постоянная составляющая сигнала калибратора U 0 = 0. После проведения калибровки ручки плавных регулировок «Вольт/дел.» и «Время/дел.» не смещать! Теоретические сведения Виды измерительных приборов Измерительные приборы разнообразны по назначению, принципу действия, метрологическим и эксплуатационным характеристикам. По форме представления измерительной информации их подразделяют на аналоговые и цифровые. Аналоговые приборы бывают электромеханическими и электронными. Электромеханический прибор состоит из измерительной цепи 1, измерительного механизма 2 и отсчетного устройства 3. Измерительная цепь 1 служит для преобразования измеряемой физической величины Х (напряжения, силы тока, мощности и т.п.) в некоторую промежуточную электрическую величину Х 1 (ток или напряжение), функционально связанную с величиной Х и непосредственно воздействующую на измерительный механизм 2 (делитель напряжения, шунт). Отсчетное устройство 3 содержит шкалу с делениями и указатель (механический – стрелка или световой – пятно). Обобщенная структурная схема такого прибора показана на рис. 2.1.
Рисунок 2.1 – Структурная схема электромеханического прибора В целях повышения чувствительности прибора, расширения диапазона измерений величин в сторону малых значений измерительная цепь содержит электронные узлы. Такие приборы, в отличие от обычных аналоговых приборов прямого преобразования, называют электронными. Цифровым называется прибор, у которого выходной сигнал является цифровым, т.е. содержит информацию о значении измеряемой величины, закодированную в цифровом коде. Структура цифрового прибора во входной части подобна структуре электронного аналогового прибора. Необходимым элементом каждого цифрового измерительного прибора является аналого-цифровой преобразователь (АЦП). АЦП – это измерительное устройство, которое осуществляет автоматическое преобразование размера выходной величины (преимущественно напряжения) входного преобразователя в её цифровое (численное) значение. На выходе цифрового прибора используется цифровое отсчетное устройство, с помощью которого через дешифратор результат измерения представляется в виде цифр и других знаков. При измерении часто используются приборы, называемые мультиметрами, предназначенные для измерений в различных диапазонах нескольких электрических величин: постоянных и переменных тока и напряжения, электрического сопротивления и т.д.
Вольтметры Аналоговые вольтметры постоянного и переменного периодического напряжения строят на базе измерительных механизмов различных типов. Измерительный механизм (ИМ) имеет следующие характеристики: Rм – сопротивление механизма, Ім – ток полного отклонения механизма и следовательно, напряжение полного отклонения стрелки механизма.
Если измеряемое постоянное напряжение превышает Uм (Ux>Uм), то включают масштабный преобразователь (делитель) измеряемого напряжения (рис. 2.2). Тогда конечное значение шкалы вольтметра будет Uк = Uм ∙Кмп. Недостатками вольтметра постоянного напряжения будут малое сопротивление между зажимами вольтметра Rv и недостаточная чувствительность.
Рис. 2.2 – Электромеханический вольтметр постоянного напряжения Электронный аналоговый вольтметр имеет большее Rv и большую чувствительность за счет включения электронного масштабного преобразователя с Кмп ≥ 1 (рис. 2.3).
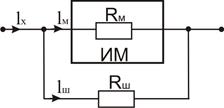
Рисунок 2.3 – Электронный вольтметр постоянного напряжения Амперметры Электрический ток в цепи может быть измерен прямыми или косвенными методами. При прямом измерении постоянного тока используется измерительный механизм, имеющий ток полного отклонения Iм и сопротивление Rм. Расширение шкалы (рис. 2.4) до значения Iх производится за счет включения шунта, сопротивление которого выбирают из условия:
. Рисунок 2.4 – Расширение шкалы амперметра При косвенном методе измерения значение тока с помощью измерительного преобразователя преобразуют в другую физическую величину, значение которой измеряют. Так, при преобразовании значения измеряемого тока в напряжение используют вольтметр, шкала которого градуируется в единицах тока.
При Rш << Rv измеряемое значение тока определится
Рисунок 2.5 – Косвенное измерение тока Виды измерений Измерение тока и напряжения в электрической цепи проводят в диапазоне частот от 0 Гц до 1 ГГц. На более высоких частотах эти величины теряют свою однозначность в линии передачи и в её поперечном сечении. По этим причинам на сверхвысоких частотах предпочитают измерять мощность, а не ток и напряжение. С точки зрения получения значения измеряемой величины по результатам первичных измерений различают прямые и непрямые (косвенные) измерения. Прямое измерение – это измерение, при котором значение величины Х получают непосредственно по показанию соответствующего прибора Х п без дополнительных расчетов Х = Х п.
Примеры прямых измерений: измерение силы тока – амперметром, напряжения – вольтметром и т.д. При непрямом (косвенном) методе измерения величину Х определяют по результатам прямых измерений величин у 1, у 2, … у п, которые связаны с нею определенной функциональной зависимостью Х = f (у 1, у 2 ,… у п). Измерение силы тока В электрическую цепь (рис. 2.7 а) прибор для измерения тока (амперметр) включается последовательно с нагрузкой RH (рис. 2.7 б). Как и при измерении напряжения, так и при измерении тока амперметром, имеющим сопротивление RA, возникаютметодическая и инструментальная погрешности.
Рисунок 2.7 – Схема включения амперметра До включения амперметра через R H протекал ток I, после включения амперметра, имеющего сопротивление R A, в цепи будет протекать измеряемый ток I И (рис. 2.8 в). До включения амперметра через R H протекал ток I, после включения амперметра, имеющего сопротивление R A, в цепи будет протекать измеряемый ток I И (рис. 2.8 в). Относительное значение методической погрешности:
Выполнив преобразования, для относительной методической погрешности получим выражение:
Из выражения видно, что методическая погрешность является систематической и её значение тем меньше, чем меньше сопротивление амперметра RA. Действительное значение тока с учетом поправки на методическую погрешность будет:
Преобразовав последнее выражение, для действительного значения тока, протекающего через RH (без включенного амперметра на рис. 7а), получим выражение:
Конечное значение результата измерения записывают в виде:
Теоретические сведения (приведены в лабораторной работе №2)
Подготовка приборов к измерению сопротивления 3.2.1. В7-26
3.2.2. Щ4313 Переключатель рода работ выставить в положение «
3.3.1 На магазине сопротивлений установить:
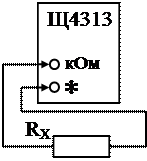
3.3.2. Подключить RX к В7-26 (рис.2) и измерить его величину. Конечное значение шкалы Rk = 3.3.3. Подключить RX к Щ4313 (рис.3) и измерить его величину.Записать значения Rизм, Rk, коэффициентов a и b (см. паспорт прибора), вычислить класс точности KП прибора. Для мультиметра Щ4313 класс точности определяется по формуле:
3.3.4. С учетом инструментальной погрешности результат измерений прибором В7-26 записать в виде:
где Rизм – измеренное значение, RK – конечное значение шкалы прибора. 3.3.5. Результат измерений прибором Щ4313 записать в виде:
3.3.6. На магазине сопротивлений установить R2 = (кОм) и выполнить пункты 2.1. - 2.5.
3.4. Измерение сопротивлений R1 и R2 косвенным методом
3.4.1. Собрать схему (рис. 4). Установить на источнике питания Е = (В).
Записать результат измерения сопротивлений R1(R2) с учетом инструментальной погрешности косвенных измерений:
Методическая погрешность измерений:
Окончательный результат измерения сопротивления:
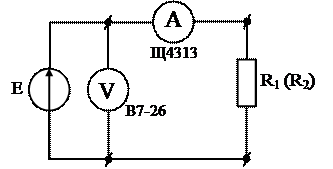
3.4.2. Собрать схему (рис. 5). Записать результаты измерений тока и напряжения:
Записать результат измерения с учетом инструментальной погрешности косвенных измерений:
Методическая погрешность измерений:
Поправка на методическую погрешность:
Случайная погрешность поправки
Результат измерения сопротивления с учетом погрешностей:
5. По полученным результатам сделать выводы. 3.4. Содержание отчета: 1. Цель работы. 2. Схема измерения. 3. Таблицы и графики результатов измерения. 4. Результаты обработки эксперимента. 5. Выводы и замечания по работе. 3.5. Контрольные вопросы: 1. Как измерить сопротивление резистора методом амперметра-вольтметра? Как при этом определить погрешность измерения сопротивления? 2. Как определить методическую погрешность измерения сопротивления методом амперметра-вольтметра? 3. Как определить погрешность измерения сопротивления омметром? ЛАБОРАТОРНА РОБОТА №4 Цель работы: изучить порядок обработки результатов многократных, равноточных наблюдений при прямых измерениях; приобрести навыки стандартной обработки результатов наблюдений, оценки погрешностей и способов представления результатов измерений. Теоретические сведения В измерительной практике для уменьшения влияния случайных погрешностей на результат измерения проводят измерения с многоразовыми наблюдениями, а затем статистически обрабатывают полученные результаты. При этом могут быть использованы различные процедуры обработки. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. Результат измерения содержит погрешность, представляющую сумму систематической составляющей DС и случайной составляющей
Эти две составляющие погрешности резко отличаются по своим свойствам. Систематическая погрешность DС остается постоянной или изменяется по определенному закону при повторных измерениях одной и той же физической величины. Она является математическим ожиданием
Обнаружение систематической погрешности – трудоемкая операция и может быть выполнена несколькими способами: 1) Проверка данного измерительного прибора с помощью образцового (более точного). При измерении одной и той же физической величины измерительным и образцовым приборами получают разные показания: X раб и X обр. Их разность является абсолютной систематической погрешностью прибора:
Тогда показания рабочего прибора корректируются введением поправки П, численно равной
При этом за результат измерения необходимо принимать величину
2) Метод замещения. В этом случае измеряемая величина 3) Метод компенсации по знаку применяется при направленном действии причины, вызывающей систематическую погрешность. Выполняют измерения так, чтобы погрешность входила с разными знаками в формулы
тогда Переменные систематические погрешности разделяют на прогрессирующие и периодические. Для устранения этих составляющих необходимо найти функциональную связь погрешности и влияющего фактора и вводить поправку на основании полученных зависимостей. Сложную задачу по выявлению и исключению систематической погрешности не всегда удается довести до конца и поэтому остается неисключенная часть систематической погрешности. Нетрудно убедиться, что результат измерения – случайная величина. Таким образом, случайная погрешность Одной из важнейших характеристик случайной погрешности является закон распределения плотности вероятности – плотность распределения вероятностей Законы распределения могут быть дискретными (для дискретных случайных величин) и непрерывными (для непрерывных величин). Дискретный закон распределения представляет совокупность значений случайной величины
Для непрерывных случайных величин с известным законом распределения
Условие нормировки для непрерывной случайной величины имеет вид:
Рисунок 4.1 – Нормальный закон распределения
Если дестабилизирующих факторов, обуславливающих случайную погрешность много (3 и более), то закон распределения плотности вероятности
Из представленного графика видно: если в состав погрешности входит систематическая составляющая
достигается при
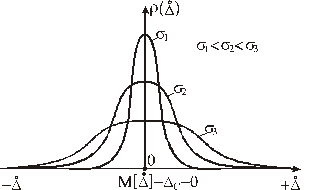
а) б) Рисунок 4.2 – Кривые Гаусса а) для разных значений систематической составляющей погрешности б) для разных значений среднеквадратического отклонения s. Характер закона распределения изменяется в зависимости от параметров s и s2 (рис. 4.2, б). Дисперсия
характеризует рассеяние случайной величины относительно среднего значения. Среднеквадратическое значения отклонения (СКО)
Дисперсия и СКО характеризуют точность измерений. Чем больше s2 и s, тем меньше точность, т.е. больше погрешность измрений. При нормальном законе распределения с
При введении нормированной случайной переменной
где Ф(z) – интеграл вероятности. Доверительная вероятность P дов при заданных граничных значениях погрешности – это вероятность нахождения случайной величины
Рисунок 4.3 – Доверительная вероятность при заданных граничных значениях погрешности Функция Ф(z) табулирована или определяется по графику (рис. 4.4).
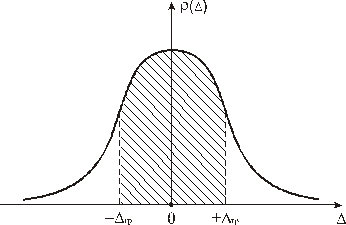
Рисунок 4.4 – Функция Лапласа для разных значений нормированной переменной Если задана P дов, то по графику или таблице находят z гр, затем определяют Dгр = z гр×s. Доверительный интервал Dдов = –Dгр … +Dгр, он с заданной вероятностью накрывает истинное значение В зависимости от целей измерений доверительную вероятность на практике устанавливают Р дов = 0,95 … 0,99. За максимальное значение погрешности, описываемой нормальным законом распределения Вероятность того, что погрешность превысит максимальное значение, определяется выражением:
означающим, что погрешность в 369 случаях из 370 попадает в интервал ±3s и лишь в одном случае выходит за эти пределы. Порядок выполнения работы 1. Измерить сопротивление n резисторов одного номинала прибором Щ 4313 в режиме омметра. Результаты наблюдений занести в табл. 4.1. 2. Предполагаем, что измеряемые значения Ri подчиняются нормальному закону распределения. Последовательность обработки результатов проводить в соответствии с методикой, изложенной в ГОСТ 8.207–76: 2.1. Вычислить среднее арифметическое значение 2.2. Вычислить разности между результатами отдельных наблюдений Ri и среднего значения При большом числе измерений сумма случайных погрешностей стремится к нулю 2.3. Рассчитать величины квадрата абсолютной погрешности Таблица 4.1
Сумма квадратов случайных погрешностей должна быть минимальной 2.4. Определить оценку среднеквадратического отклонения результатов каждого из n одноразовых наблюдений 2.5. Исключить аномальные результаты (грубые промахи) по критерию «трех сигм». Для этого из ряда значений D i найти наибольшие и сравнить их с 2.6 Найти оценку СКО среднего арифметического значения 2.7. Определить доверительные границы случайной составляющей погрешности и записать результат измерений. Если за результат измерений принято среднее значение
При Р дов = 0,997 z гр = 3 и При любой другой доверительной вероятности Р дов можно воспользоваться табличным (или из графика) значением интервала вероятности Ф(z) = Р дов, по его значению можно найти z гр и далее, так как
2.8. В случае, если число измерений n мало 2.9. Учитывая, что систематическая погрешность DС вошла в состав результата измерений
где g – класс точности прибора, %. Для прибора Щ 4313 относительная погрешность определяется по формуле:
где a и b – коэффициенты, зависящие от конечного значения шкалы R к. Согласно паспортным данным прибора Щ4313, при R к = 500 Ом, a = b = 1,5. При R к = 5 кОм и более, a = b = 0,5. Абсолютная погрешность: В случае, если
Числовое значение результата измерения должно заканчиваться цифрой того же порядка, что и значение погрешности D. При этом число значащих цифр при определении D не должно превышать двух. 3. Определить закон распределения погрешностей результатов измерений. Для идентификации закона распределения необходимо построить гистограмму (
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.79 (0.018 с.) |


 – временной интервал, в течение которого сигнал увеличивается от уровня 0,1 Um до уровня 0,9 Um;
– временной интервал, в течение которого сигнал увеличивается от уровня 0,1 Um до уровня 0,9 Um; – временной интервал, в течение которого сигнал уменьшается от уровня 0,9 Um до уровня 0,1 Um;
– временной интервал, в течение которого сигнал уменьшается от уровня 0,9 Um до уровня 0,1 Um; .
. .
.
 Например.
Например. =1/2000 Гц =
=1/2000 Гц = ;
; ;
; .
.
 .
.



 .
.

 , где
, где ,
, 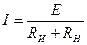 .
. .
.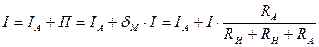 ,
, .
. .
.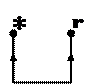 Переключатель рода работ перевести в положение «r» и проверить нулевое положение указателя при замкнутых накоротко гнездах «r» и «*» (рис. 3.1). Затем разомкнуть гнезда и установить указатель (стрелку) в положение «∞» на шкале
Переключатель рода работ перевести в положение «r» и проверить нулевое положение указателя при замкнутых накоротко гнездах «r» и «*» (рис. 3.1). Затем разомкнуть гнезда и установить указатель (стрелку) в положение «∞» на шкале  ручкой «Устан. “∞”» (для
ручкой «Устан. “∞”» (для  ». Выбрать шкалу прибора.
». Выбрать шкалу прибора.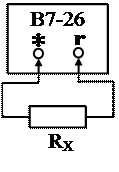 3.3. Измерение сопротивлений прямым методом
3.3. Измерение сопротивлений прямым методом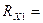 (Ом),
(Ом), 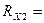 (кОм).
(кОм).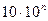 Ом (10n – множитель шкалы). Записать Rизм, Rk, KП.
Ом (10n – множитель шкалы). Записать Rизм, Rk, KП.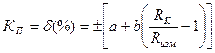 .
.
 ,
,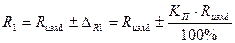 .
.
 ,. RV = 30 МОм, IK – конечное значение шкалы. Записать результаты измерений тока и напряжения в виде:
,. RV = 30 МОм, IK – конечное значение шкалы. Записать результаты измерений тока и напряжения в виде: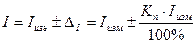 ,
,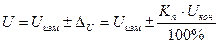 .
.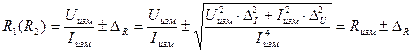 .
.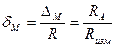 ,
,  . Поправка П = -RA.
. Поправка П = -RA.

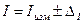 ;
;  .
. .
.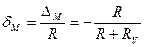 ;
;  .
.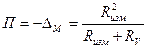 .
.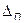 :
: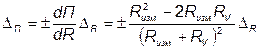 .
.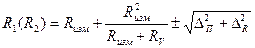 .
. :
: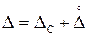 .
.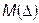 погрешности D измерения
погрешности D измерения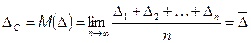 .
.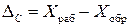 .
.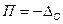 .
.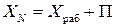 .
.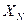 заменятся известной величиной
заменятся известной величиной 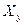 таким образом, чтобы показание прибора осталось неизменным. Тогда результат измерения
таким образом, чтобы показание прибора осталось неизменным. Тогда результат измерения  .
. ;
; 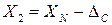 ,
,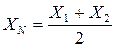 .
.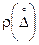 или
или  – функция распределения вероятностей.
– функция распределения вероятностей.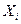 и соответствующих им вероятностей
и соответствующих им вероятностей  . Условие нормировки закона распределения вероятностей дискретной случайной величины:
. Условие нормировки закона распределения вероятностей дискретной случайной величины: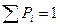 .
. вероятность того, что данная случайная величина
вероятность того, что данная случайная величина 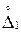 до
до  , определяется площадью, ограниченной этой кривой и осью абсцисс (рис. 4.1), т.е.
, определяется площадью, ограниченной этой кривой и осью абсцисс (рис. 4.1), т.е.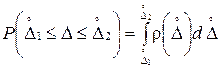 .
.
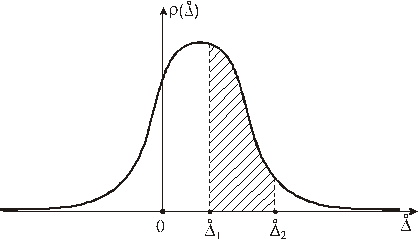
 .
.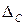 , то закон распределения плотности вероятности будет смещен на эту величину. Если же систематическая погрешность исключена
, то закон распределения плотности вероятности будет смещен на эту величину. Если же систематическая погрешность исключена 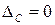 (М[D] = 0), то
(М[D] = 0), то  и максимальное значение такой кривой Гаусса
и максимальное значение такой кривой Гаусса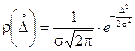
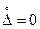 (рис. 4.2.б).
(рис. 4.2.б).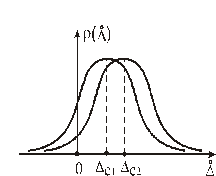
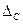
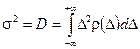
 .
. .
.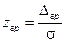 выражение P (D) преобразуется к виду:
выражение P (D) преобразуется к виду: ,
,

 , Р дов = …
, Р дов = …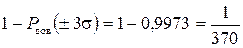 ,
, измеряемой величины
измеряемой величины 
 . Значение D i занести в табл. 4.1. Определить сумму всех погрешностей
. Значение D i занести в табл. 4.1. Определить сумму всех погрешностей  .
. . Этот вывод основывается на аксиоме случайности теории случайных погрешностей, что при очень большом числе измерений и при отсутствии систематических DС погрешностей, положительные и отрицательные погрешности встречаются одинаково часто.
. Этот вывод основывается на аксиоме случайности теории случайных погрешностей, что при очень большом числе измерений и при отсутствии систематических DС погрешностей, положительные и отрицательные погрешности встречаются одинаково часто. , результаты занести в табл. 4.1.
, результаты занести в табл. 4.1.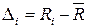

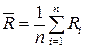


 .
. . Такой критерий надежный при числе измерений
. Такой критерий надежный при числе измерений  . Если
. Если  , то подозреваемый в аномальности результат Dmax исключить, а затем повторить сначала расчеты по пунктам 2.1. – 2.4.
, то подозреваемый в аномальности результат Dmax исключить, а затем повторить сначала расчеты по пунктам 2.1. – 2.4. .
.
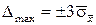 .
. , можно определить Dгр и записать результат
, можно определить Dгр и записать результат
 , то
, то  ,
, ,
, ,
, .
. , то неисключенной систематической погрешностью пренебрегают и принимают D = Dгр; если
, то неисключенной систематической погрешностью пренебрегают и принимают D = Dгр; если  , то пренебрегают случайной погрешностью и считают, что D = DС. В случае равенства
, то пренебрегают случайной погрешностью и считают, что D = DС. В случае равенства  вычисляют
вычисляют  ,
,  , и тогда
, и тогда  , а результат представляют в виде:
, а результат представляют в виде:


