
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С помощью математического маятникаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: экспериментальное определение ускорения свободного падения при помощи математического маятника Приборы и принадлежности: лабораторная установка «Математический маятник», секундомер. Материал для изучения: раздел «Гармонические колебания». 1. Основные понятия и определения Математический маятник – идеализированная система, состоящая из материальной точки массой Колебания – это движения или процессы, которые характеризуются определенной повторяемостью во времени. Свободные колебания – колебания, которые совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Обсудим гармонические колебания на примере тела массой m, прикрепленного к поверхности стены пружиной жесткостью k (рис. 1). Если деформация пружины подчиняется закону Гука
С помощью определения ускорения
Уравнение (1) имеет решения в виде гармонических функций вида
где А – амплитуда колебаний (максимальное значение колеблющейся величины), В общем случае уравнение свободных гармонических колебаний принято записывать в виде:
С помощью решения уравнения гармонических колебаний достаточно легко определить основные характеристики движения: скорость и ускорение:
Следовательно, в моменты времени, когда x =0, скорость приобретает наибольшее значение, когда же x достигает максимального отрицательного значения, то ускорение приобретает максимальное положительное значение. Период гармонического колебания – промежуток времени Т, в течение которого фаза колебаний получает приращение 2p, т.е.
откуда
Частота колебаний – число полных колебаний, совершаемых в единицу времени.
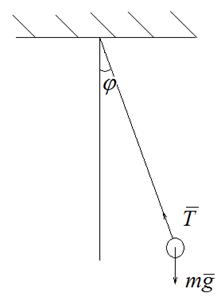
Теоретическое введение Ускорение свободного падения тел можно измерить несколькими методами, в частности, методом математического маятника. Метод математического маятника является одним из наиболее простых и точных методов измерения ускорения свободного падения тел вблизи поверхности Земли. Физической моделью математического маятника является маятник, состоящий из тяжелого шара массой m, подвешенного на длинной стальной нити длиной l (рис.2).
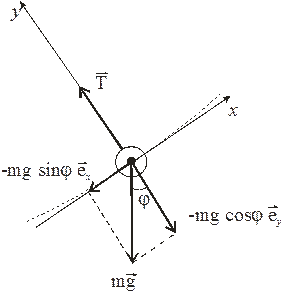
Рисунок 2 Математический маятник. Рисунок 3 Силы, действующие на тело, подвешенное на нити в поле тяжести.
С помощью второго закона Ньютона может быть записано уравнение движения для математического маятника (рис.3):
где Определим проекции сил в уравнении (4) на мгновенные оси OX и OY:
Поскольку нить является нерастяжимой, то в случае малых колебаний Проекция ускорения на ось OX может быть связана с угловым ускорением (при условии нерастяжимости нити):
Подставляя уравнение (6) в первое уравнение системы (5)
или
Решения уравнения (8) в общем случае представляются через эллиптические функции Якоби либо Вейерштрасса. В частном случае, когда амплитуда колебаний маятника мала, а угол отклонения
Решения (8а) представляются через гармонические функции:
где A - амплитуда, Отметим, что амплитуда колебаний A определяется только начальным отклонением и не зависит от циклической частоты колебаний маятника Период колебаний математического маятника связан с угловой частотой выражением:
Из полученного выражения находим связь ускорения свободного падения и характеристик математического маятники (длины нити l и периода колебаний T):
Методика измерений Упражнение 1. Определение периода изохронности маятника. Для определения периода изохронности колебаний маятника необходимо провести измерения периода колебаний для 10 различных амплитуд. Определить период изохронности колебаний с точностью до 1%. Упражнение 2 Определение ускорения свободного падения. Для определения величины ускорения свободного падения необходимо 10 раз измерить величину периода колебаний. Полученные данные занести в табл. 1: Таблица 1
Здесь Затем, используя выражение
где Затем по формуле (11) вычислить ускорение свободного падения, подставив среднее значение периода и измеренную длину маятника. Результат записать в виде: 4. Контрольные вопросы: 1. Что такое математический маятник? Получите уравнение колебаний математического маятника для случая малых углов отклонения от положения равновесия. 2. Что такое колебание, гармоническое колебание? 3. Дайте определение амплитуде, частоте, фазе, периоду колебаний. 4. Чему равна скорость и ускорение точки, если она совершает гармоническое колебание? 5. Будет ли изменяться частота (период) колебаний математического маятника, если изменить массу груза (амплитуду, длину нити)? 6. Выведете расчетную формулу для нахождения величины ускорения свободного падения. 7. Что такое диапазон изохронности математического маятника? Лабораторная работа №4
Цель работы: экспериментальное определение момента инерции тела вращения, изучение уравнения вращательного движения. Приборы и принадлежности: маятник Максвелла, набор металлических накладных колец (массу колец и погрешность определения массы уточнить у инженера).
Материал для изучения: Динамика вращательного движения. Момент инерции.
1. Основные понятия и определения С основными понятиями и определениями динамики вращательного движения можно ознакомиться во вводной части к лабораторной работе №2 настоящего методического пособия.
Теоретическое введение Маятник Максвелла - это колебательная система (рис. 1), которая состоит из кронштейна, на котором бифилярно на тонких нерастяжимых нитях подвешен стержень (шкив) с небольшим диском туго насаженным на стержень (маховиком). Маятник Максвелла предназначен для изучения законов вращательного движения и определения моментов инерции тел, закрепляемых на маховике. Рассмотрим принцип действия маятника Максвелла. Пусть в начальный момент времени нить намотана на ось маховика, который при этом располагается вблизи точки подвеса. Под действием силы тяжести маховик будет опускаться вниз. Нити во время движения разматываются до полной длины, раскрутившийся маховик продолжает вращательное движение в том же направлении и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом вращение. Дойдя до верхней точки, диск опять опускается вниз и т.д. Маховик будет совершать колебания вверх и вниз, поэтому устройство и называют маятником.
Рисунок 1 Схематичное изображение Рисунок 2 Силы действующие маятника Максвелла на маятник Максвелла
Установим связь между ускорением поступательного движения маятника Максвелла и моментом инерции. Введем следующие обозначения: (рис. 2) mg — сила тяжести; T — сила натяжения одной нити; r — радиус шкива, на который наматываются нити; тогда уравнение для поступательного движения можно записать так: ma =mg - 2T, (1) где a — ускорение центра масс, а уравнение для вращательного движения. Поскольку сила тяжести приложена к центру масс, вращающегося маховика, а само вращение происходит вокруг оси проходящей через центр масс, то момент сил M связан только с силами натяжения обеих нитей (для силы тяжести он равен нулю). M =2Tr (2) где M — момент действующих сил. Выражая из уравнения (1) силу натяжения нитей получим окончательное выражение для момента сил. M = mr (g - a)(3) В соответствии с основным уравнением динамики вращательного движения: Ie = M, (4) где e - угловое ускорение, I - момент инерции маховика. Поскольку проходимый маятником путь в единицу времени соответствует длине разматываемой (наматываемой) на шкив нити за то же время, то можно записать уравнение, связывающее скорость поступательного движения v и угловую скорость w: v = r w или для ускорения a = r e. Таким образом, может быть записано соотношение:
Из выражения (5) может быть найдено выражение для ускорения a:
Как видно из формулы (5), движение происходит с постоянным ускорением, которое зависит радиуса шкива, на который намотана нить и момента инерции тела. Отметим, что момент инерции всегда пропорционален массе тела I ~ m. Например, для диска момент инерции составляет ½ mR 2. Таким образом, ускорение с которым движется маятник Максвелла, не зависит от его массы, а зависит только от радиуса маховика R и радиуса шкива r. Зная ускорение а, из формулы (6) можно определить момент инерции I маятника:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.127 (0.009 с.) |

 , подвешенной на длинной, нерастяжимой и невесомой нити, и колеблющаяся под действием силы тяжести.
, подвешенной на длинной, нерастяжимой и невесомой нити, и колеблющаяся под действием силы тяжести. , то в соответствии со вторым законом Ньютона может быть записано уравнение:
, то в соответствии со вторым законом Ньютона может быть записано уравнение:

 уравнение движения может быть переписано в виде:
уравнение движения может быть переписано в виде: (1)
(1) . (2)
. (2) - круговая или циклическая частота,
- круговая или циклическая частота,  - начальная фаза в момент времени
- начальная фаза в момент времени  ,
,  - фаза колебаний в момент времени t. Подстановкой решения (2) в уравнение (1) можно получить связь циклической частоты
- фаза колебаний в момент времени t. Подстановкой решения (2) в уравнение (1) можно получить связь циклической частоты  .
. (3)
(3) .
. .
. ,
, .
. ,
,  .
.
 , (4)
, (4)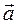 - ускорение маятника,
- ускорение маятника,  - сила натяжения нити.
- сила натяжения нити. (5)
(5) .
. (6)
(6) , (7)
, (7) (8)
(8) , и уравнение (8) можно представить в виде:
, и уравнение (8) можно представить в виде: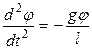 . (8а)
. (8а) (9)
(9) - циклическая частота колебаний маятника,
- циклическая частота колебаний маятника,  - начальная фаза.
- начальная фаза. . Это означает, что для маятников имеющих разную амплитуду, но одинаковые длины нити l, частота колебаний будет одинаковой. Кроме того, частота
. Это означает, что для маятников имеющих разную амплитуду, но одинаковые длины нити l, частота колебаний будет одинаковой. Кроме того, частота  (10)
(10) . (11)
. (11)


 - среднее значение периода колебаний.
- среднее значение периода колебаний. , необходимо найти дисперсию
, необходимо найти дисперсию  . Результат записать в виде:
. Результат записать в виде: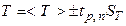 ,
, - коэффициент Стьюдента (определяемый из таблиц [4] для доверительной вероятности p =0.95 и количества измерений n = 10).
- коэффициент Стьюдента (определяемый из таблиц [4] для доверительной вероятности p =0.95 и количества измерений n = 10). . Здесь
. Здесь  - погрешность косвенного измерения, рассчитанная по аналогии с [4].
- погрешность косвенного измерения, рассчитанная по аналогии с [4]. МАЯТНИК МАКСВЕЛЛА
МАЯТНИК МАКСВЕЛЛА
 (5)
(5) (6)
(6) (7)
(7)


