
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические распределения в молекулярной физикеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Ознакомление с основными статистическими закономерностями идеальных газов. Приборы и принадлежности: персональный компьютер, программа LabStat.exe Материал для изучения: основные понятия теории вероятности (вероятность, плотность вероятности, нормировка вероятности, биноминальное распределение, распределение Гаусса), распределение Максвелла.
1. Теоретическое введение. Основные определения В молекулярной физике изучается поведение систем, состоящих из большого числа частиц. Обычно в 1см3 твердого тела содержится 1022 -1023 атомов. Уравнения классической механики не могут быть использованы для описания таких систем, т.к. это требует решения системы дифференциальных уравнений
В соответствии вероятностным подходом некоторые физические величины, характеризующие конкретные частицы (такие как координаты, импульс, энергию), имеют случайные значения. Такие величины в теории вероятностей называют случайными. Случайная величина – величина, значение которой нельзя предсказать заранее. Для описания случайных величин вводится понятие вероятности, которое мы обсудим на примере молекулы, находящейся в объеме V (рис.1). Пусть частица случайным образом блуждает в объеме V, и выйти за пределы этой области не может. Предположим, что мы проводим N ex экспериментов, результатом, которых является проверка наличия одной частицы в объеме V 1. Если из всех N ex экспериментов N 1, соответствует такому событию, тогда по определению вероятностью называется величина P (V 1):
Если случайная величина может принимать дискретный набор значений, то ее характеризуют набором вероятностей всех возможных событий Обсудим одно из важнейших свойств распределения вероятностей, на примере блуждающей частицы в объеме V. Если в пределах объема V выделить несколько непересекающихся элементов объема Vi, тогда можно ввести вероятности попадания в каждый из них Pi по аналогии с (1)
Если
Характер распределения вероятностей
Из этого следует, что вероятность
Во многих случаях приходится работать со случайными величинами, которые могут принимать непрерывные значения (например, координаты частиц). В этом случае распределение вероятностей записывается с помощью функции называемой плотностью вероятности f (x), которая устанавливает связь между вероятностью и интервалом изменения случайной величины. Вероятность такого события, что случайная величина x лежит в пределах (x 0, x 0+ dx) определяется формулой:
Вероятность того, что случайная величина x лежит в пределах от x 1 до x 2 определяется интегралом:
Условие нормировки (2) для случая непрерывного изменения случайной величины x переписывается в виде
где интегрирование ведется по всей области определения случайной величины
Независимые события Определим вероятность события, когда в одном из измерений частица попадает в объем
В случае непрерывных случайных величин x и y плотность вероятности
Биноминальное распределение Рассмотрим систему объемом V, в которой находится N частиц. Определим вероятность события, в соответствии с которым ровно m частиц попадают в объем V 1. Вероятность того, что m частиц попали в объем V 1, в соответствии с (3) и (7):
При этом остальные
Следует учесть, что все частицы в системе одинаковы и обладают идентичными свойствами (неразличимы). Это означает, что m частиц могут быть выбраны из полного числа N произвольным образом. Количество способов выбрать m частиц из полного набора N задается формулой:
Таким образом, пользуясь теоремой об умножении вероятностей (7) и соотношениями (9-11) получим выражение для вероятности
Выражение (12) называется биноминальным распределением. С помощью бинома Ньютона для распределения (12) может быть легко проверено выполнение условия нормировки (2)
где использовано определение
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1085; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 , количество уравнений при этом совпадает с числом частиц в системе. Очевидно, что такая система уравнений не может быть решена для реальных систем, поэтому чаще всего для описания используется вероятностный подход, изучаемый статистической физикой.
, количество уравнений при этом совпадает с числом частиц в системе. Очевидно, что такая система уравнений не может быть решена для реальных систем, поэтому чаще всего для описания используется вероятностный подход, изучаемый статистической физикой. Вероятность
Вероятность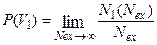 (1)
(1) , называемым распределением вероятностей.
, называемым распределением вероятностей. (1a)
(1a) , тогда очевидно, что
, тогда очевидно, что  , а для вероятностей выполняется условие нормировки:
, а для вероятностей выполняется условие нормировки: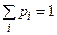 (2)
(2) , где A – константа, определяемая из условия нормировки (2):
, где A – константа, определяемая из условия нормировки (2): ,
,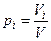 . (3)
. (3) (4)
(4) , (5)
, (5) , (6)
, (6) .
. , а при другом измерении частица попадает в другой объем
, а при другом измерении частица попадает в другой объем  . Вероятность такого события определяется теоремой об умножении вероятностей:
. Вероятность такого события определяется теоремой об умножении вероятностей: (7)
(7) определяется произведением функций плотности вероятности для каждой из случайных величин (
определяется произведением функций плотности вероятности для каждой из случайных величин ( ):
): (8)
(8) (9)
(9)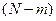 частиц должны попасть в объем
частиц должны попасть в объем  . Вероятность этого события:
. Вероятность этого события: (10)
(10) (11)
(11) :
: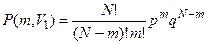 (12)
(12) (13)
(13) .
.


