
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление средних значений физических величинСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для характеристики случайной величины часто пользуются понятием среднего значения, которое определяется как:
Мерой отличия случайной величины x от среднего значения
Раскрывая скобки и пользуясь определением средних величин можно получить простое выражение для расчета дисперсии:
В качестве примера рассчитаем средние значения и дисперсию для биноминального распределения. Установим среднее значение числа частиц попадающих в область V 1 -
Для расчета дисперсии биноминального распределения воспользуемся формулой (15) и результатом вычисления
Подстановка этой формулы в (15) приводит к значению дисперсии в биноминальном распределении:
Вычисление средних значений физических величин, зависящих от случайной величины x, проводится аналогично (14). Если известны вероятности различных состояний системы pi, при этом требуется вычислить значения какой-либо физической величины u имеющей разные значения в каждом из состояний ui=u (xi). Вычисление среднего значения
В случае непрерывного распределения вероятности выражение для среднего значения величины u (x) определяется через функцию плотности вероятности f (x):
Распределение Гаусса Распределение Гаусса достаточно часто встречается при описании реальных физических систем. Одной из основных задач, приводящих к получению распределения Гаусса, является задача о случайном блуждании частицы на плоскости. Если частица начинает блуждания из начала координат, то вероятность ее обнаружения через некоторое время в области площадью dxdy в окрестности точки (x 0, y 0), определяется в виде:
где функция f (x) - распределение Гаусса для случайной величины x:
Здесь
Распределение Максвелла Распределение Максвелла определяет функцию распределения частиц идеального газа по скоростям. По своему виду распределение Максвелла совпадает с распределением Гаусса, когда в качестве случайных величин выбираются проекции скорости молекул. Функция плотности вероятности для проекции скорости
Поскольку компоненты скорости являются независимыми, то выражение (17) может быть перенесено и на компоненты скорости В соответствии с (17) может быть получено распределение по модулю скорости:
График функции F (v) зависит от температуры Распределение Максвелла F (v) может быть охарактеризовано несколькими характерными значениями скорости:
Вычисление среднего значения кинетической энергии молекул идеального газа, описываемых распределением Максвелла, может быть получено в виде:
Методика моделирования Рассмотрим N частиц, идеального газа, имеющих одинаковую массу m, находящихся в закрытом сосуде. Каждая из частиц характеризуется вектором скорости Предположим, что в начальный момент времени частицы идеального газа являются неподвижными. Поскольку частицы являются неподвижными, то кинетическая энергия равна нулю, а, следовательно, и температура, соответствующая такому состоянию, равна нулю (см. формулу (19)). Если частицы газа взаимодействуют с поверхностью сосуда (посредством абсолютно упругого удара, т.е. условие идеальности газа не нарушается), находящегося при некоторой температуре Tсосуда, то температура газа постепенно увеличиваться до тех пор пока не будет достигнуто состояние термодинамического равновесия и температура газа не станет равной Tгаза=Tсосуда. При каждом акте соударения со стенками сосуда происходит случайное изменение проекций импульса частиц газа. Предположим, что при каждом соударении (либо между собой, либо со стенками сосуда) изменяется только одна из проекций импульса на некоторую малую случайную величину D p. Таким образом, в системе реализуется случайное блуждание частиц из начального состояния (vxi =0, vyi =0, vzi =0) с постоянным шагом D p/m. При чем на каждом шаге изменяется только одна из проекций скорости. Так как температура газа имеет связь со средней кинетической энергией, то случайное блуждание в пространстве импульсов прекращается при достижении термодинамического равновесия со стенками сосуда (т.е. при равенстве температуры газа и температуры сосуда):
В результате расчета распределение частиц по скоростям будет соответствовать распределению Максвелла, записанному в формулах (17) и (18).
3. Практические задания Выполнение работы с помощью программы LabStat.exe. Внешний вид программы представлен на рис.4. Для выполнения упражнений 1-3 необходимо выбрать соответствующую кнопку в диалоговом окне программы.
Рисунок 4 Внешний вид программы LabStat.exe Первые два упражнения являются ознакомительными, поскольку позволяют с помощью вычислительного эксперимента познакомиться с некоторыми закономерностями теории вероятностей, применяемыми в молекулярной физике. В третьем упражнении предлагается проведение моделирования распределения частиц по проекции скорости и модулю скорости (распределение Максвелла).
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.36 (0.007 с.) |

 (14)
(14) является дисперсия (среднеквадратичное отклонение), которая определяется как:
является дисперсия (среднеквадратичное отклонение), которая определяется как: (15)
(15) (16)
(16) . По определению среднее значение
. По определению среднее значение .
. можно провести аналогично
можно провести аналогично 

 производится в соответствии с формулой:
производится в соответствии с формулой: (17)
(17) (15)
(15)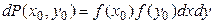
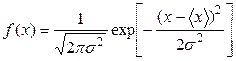 (16)
(16) - среднеквадратичное отклонение случайной величины x. График функции f (x) приведен на рис.2
- среднеквадратичное отклонение случайной величины x. График функции f (x) приведен на рис.2
 :
: (17)
(17) и
и  . Общий вид графика функции (17) соответствует зависимости представленной на рис. 2.
. Общий вид графика функции (17) соответствует зависимости представленной на рис. 2. (18)
(18) ,
, где
где  - среднее значение модуля скорости,
- среднее значение модуля скорости,  - наиболее вероятное значение скорости,
- наиболее вероятное значение скорости,  - среднеквадратичное значение модуля скорости.
- среднеквадратичное значение модуля скорости. (19)
(19) или проекциями скоростей vxi, vyi, vzi.
или проекциями скоростей vxi, vyi, vzi. .
.



