
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика измерений. Ход выполнения работыСодержание книги Поиск на нашем сайте
Используемая в работе для определения момента инерции тел вращения установка «Маятник Максвелла» на рис. 1. На основании 1 закреплена стойка 2, к которой прикреплены неподвижный верхний кронштейн 3 и подвижный кронштейн 4. На верхнем кронштейне находится электромагнит 5, фотоэлектрический датчик №1 (6) и вороток с фиксатором 7 для закрепления и регулировки длины бифилярного маятника. Нижний кронштейн 4 с фотодатчиком №2 (8) можно перемещать вдоль стойки и фиксировать в выбранном положении. Маятник 9 — это диск, закрепленный на оси и подвешенный на бифилярном подвесе. На диск накладываются сменные металлические кольца 10, изменяющие момент инерции системы. Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале стойки прибора. Сигналы с фотодатчиков служат для автоматического пуска и остановки миллисекундомера 11. Для определения момента инерции стального кольца (указанного преподавателем) необходимо с помощью лабораторной установки определить время, в течение которого произошло опускание маховика от верхней до нижней точки движения. Далее с помощью формулы Для определения времени опускания необходимо воспользоваться следующим алгоритмом проведения эксперимента: 1. На диск маятника наложить стальное кольцо. 2. Убедиться, что край стального кольца находится примерно на 2 мм ниже оптической оси нижнего фотоэлектрического датчика. Если нет, отрегулировать высоту нижнего кронштейна с фотоэлектрическим датчиком. 3. Намотать на ось маятника нить подвеса, укладывая ее равномерно, виток к витку. Проверить, отвечает ли нижняя грань кольца нулю на стойке. Если нет, ослабить фиксацию верхнего кронштейна, отрегулировать его высоту и еще раз вернуться к п.2. 4. Включить кнопку «Сеть». 5. Нажать клавишу «Пуск» миллисекундомера. 6. Намотать на ось маятника нить подвески. 7. Зафиксировать маятник с помощью электромагнита, не слишком туго закручивая нить. 8. Повернуть маятник в направлении движения на угол около 5o. Последовательно нажать клавиши «Сброс» и «Пуск». 9. Считать показания миллисекундомера 11.
4. Практическое задание Упражнение: Определение момента инерции маятника Максвелла. 1. С помощью штангенциркуля измерить радиус шкива r. Измерения провести 10 раз в различных местах шкива и занести в табл.1. По измеренным результатам определить среднее значение радиуса шкива Таблица 1
2. Установите нижний кронштейн на отметке, заданной преподавателем. Проведите 10 замеров времени падения маятника. Экспериментальные данные занесите в табл. 2. Определить среднее время падения маятника Так как падение маятника осуществляется с постоянным ускорением, то высота падения h связана с ускорением формулой a = 2 h/t2. Необходимо определить среднее значение ускорения Таблица 2
3. С помощью формулы (7) и найденного значения ускорения 4. Сделать выводы относительно точности метода определения момента инерции тела с помощью маятника Максвелла.
5. Контрольные вопросы 1. Что такое абсолютно твердое тело, вращательное движение твердого тела? 2. Дайте определение угловой скорости и угловому ускорению. Как связано ускорение поступательного движения маятника с его угловым ускорением? 3. Дайте определение момента инерции твердого тела 4. Дайте определение момента силы, момента инерции, момента импульса 5. Сформулируйте основное уравнение динамики вращательного движения. 6. Выведите расчетную формулу момента инерции. 7. Сформулируйте и докажите теорему Гюйгенса-Штейнера. 8. Выведите формулу для определения энергии вращательного движения твердого тела 9. Сформулируйте закон сохранения момента импульса при вращательном движении твердого тела. 10. Какие величины характеризуют динамику вращательного движения? 11. Вывести рабочую формулу для определения момента силы реакции нити относительно центра инерции маятника. Лабораторная работа №5
Цель работы: Ознакомление с методом определения отношения удельных теплоемкостей газов. Приборы и принадлежности: лабораторная установка, ручной насос, часы
Материал для изучения: Первое начало термодинамики, идеальные газы, уравнение состояния идеального газа, теплоемкость, изопроцессы в идеальных газах.
1. Основные понятия и определения Термодинамической системой называется система, состоящая из большого числа частиц (обычно > 1022), находящейся в ограниченной области пространства и характеризуемой температурой, давлением и плотностью (концентрацией) вещества. Равновесным состоянием (или просто состоянием) называется состояние термодинамической системы, характеризуемое значениями температуры, давления, плотности (концентрации) одинакового по всему объему системы, при этом такое состояние может сохраняться неограниченно долго. Равновесным процессом (или просто процессом) называется последовательный переход от одного равновесного состояния к другому равновесному состоянию. При этом все промежуточные состояния являются равновесными. Циклическим процессом называется процесс, начальное и конечное состояния которого совпадают. Идеальным газом называется такой газ, атомы которого при движении испытывают только абсолютно упругие столкновения между собой, а другими видами взаимодействия между частицами газа можно пренебречь. Внутренней энергией термодинамической системы называется энергия U, которая включает в себя энергию движения (кинетическая энергия частиц) и энергию взаимодействия между частицами (потенциальная энергия взаимодействия). Размерность – Дж. Следствие 1: Внутренняя энергия идеального газа связана только с энергией движения (кинетической энергией) атомов. Следствие 2: Внутренняя энергия является функцией состояния U = U (p, n,T). Теплота Q – энергия, которой система обменивается с окружающей средой. Размерность- Дж. Теплоемкостью тела называется величина, которая показывает взаимосвязь между количеством переданной телу теплоты и соответствующим изменением температуры Замечание1: Теплоемкость чаще всего зависит от температуры, давления и плотности и в разных процессах может иметь разные значения. Замечание 2: В качестве индекса у теплоемкости чаще всего указывают величину, которая не изменяется в данном процессе (CV – молярная теплоемкость при постоянном объеме). Уравнением состояния называется уравнение, которое устанавливает взаимосвязь между температурой, давлением и концентрацией вещества. Наиболее простым уравнением состояния является уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):
Замечание: уравнение Менделеева-Клапейрона применяется только к идеальному газу и не может применяться к системам, в которых нельзя пренебречь взаимодействием между частицами. Теоретическое введение Одним из основных положений термодинамики является первое начало термодинамики, которое по своей сути является законом сохранения энергии, сформулированным для систем большого числа частиц. В соответствии с первым началом термодинамики Сообщенное системе тепло Q может быть израсходовано либо на увеличение ее внутренней энергии U, либо на совершение системой работы A. Математически первое начало термодинамики для бесконечно-малых изменений этих величин записывается в виде
Для идеального газа работа и изменение внутренней энергии могут быть записаны с помощью формул:
Объединяя уравнения (1-3) получим систему уравнений, описывающую большинство явлений в идеальных газах:
Изотермический процесс Изотермическим называется процесс, в котором температура не изменяется (T = const). Тогда для идеального газа изменение внутренней энергии равно нулю dU = 0, а все тепло, передаваемое системе, расходуется на совершение работы. Из системы уравнений (4) следует:
При этом ввиду постоянства температуры приводит к зависимости
Уравнение изотермического процесса записанного в виде Изохорный процесс Изохорным процессом называется процесс, протекающий при постоянном объеме (V=const). Для такого процесса работа идеального газа оказывается равной нулю dA=pdV =0. Для такого процесса внутренняя энергия U изменяется в соответствии с теплообменом с окружающей средой. Из системы уравнений (4) следует:
Из уравнения состояния идеального газа следует, справедливость соотношения:
Из последнего уравнения следует, что для любого состояния в изохорном процессе может быть записано соотношение Изобарный процесс Процесс, протекающий при постоянном давлении, носит название изобарного процесса. В случае постоянного давления система уравнений (4) принимает вид:
В случае изобарного процесса элементарная работа
Тогда для молярной теплоемкости при постоянном давлении может быть записано выражение:
Последнее выражение принято называть соотношением Майера. Адиабатный процесс Адиабатным называется процесс, если система не обменивается теплом с окружающей средой, т.е. dQ = 0. Для этого случая система уравнений (4) имеет вид:
Если подставить в первое уравнение выражение для давления из второго, то получим следующее выражение:
Разделяя переменные в этом дифференциальном уравнении можно получить соотношение:
Интегрируя последнее уравнение, получим выражение:
или
Пользуясь уравнением состояния идеального газа из уравнения (14) можно получить уравнение адиабатного процесса в параметрах p-V.
Параметр Методика измерений Величина отношения теплоемкости при постоянном давлении (Ср)к теплоемкости при постоянном объеме (СV)для газов играет очень большую роль при адиабатических процессах и при процессах, близких к ним. Для примера укажем, что ею, в частности, определяется скорость распространения звука в газах, от нее зависит течение газов по трубам со звуковыми скоростями и достижение сверхзвуковых скоростей в расширяющихся трубах. Описываемый ниже способ определения отношения удельных теплоемкостей газов Пусть мы имеем стеклянный сосуд, соединенный с манометром. Посредством крана сосуд может соединяться с атмосферой, и пусть первоначально в нем было атмосферное давление. Если с помощью насоса накачать в сосуд небольшое количество воздуха и закрыть кран, то давление в сосуде, конечно, повысится; но если это повышение было произведено достаточно быстро, манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим, и следовательно, температура его повысилась (в действительности же нагнетание воздуха занимает некоторое время, поэтому процесс этот нельзя считать строго адиабатическим). Окончательная разность уровней в манометре (h1) установится только тогда, когда температура воздуха внутри сосуда сравняется благодаря теплопроводности стенок с температурой окружающего воздуха. Обозначим через T1 абсолютную температуру окружающего воздуха и через р1 — давление газа внутри сосуда, соответствующее показанию манометра h1; совершенно ясно, что р1 = р0 + h1, (15) где р0 — атмосферное давление (конечно, при этом р0 и h1 должны быть выражены в одинаковых единицах). Эти два параметра T1 и р1 характеризуют состояние газа, которое мы назовем первым состоянием газа (состояние I: T1, р1). Если теперь быстро открыть кран, то воздух в сосуде будет расширяться адиабатически, пока давление его не сделается равным р0; при этом он охладится до температуры T2; это будет вторым состоянием газа (состояние II: Т2, р0). Если сразу после открывания снова закрыть кран, то давление внутри сосуда начнет возрастать вследствие того, что охладившийся при расширении воздух в сосуде станет снова нагреваться. Возрастание давления прекратится, когда температура воздуха в сосуде сравняется с внешней температурой T1 это будет третьим состоянием газа (состояние III: T1, р2). Обозначим давление воздуха в сосуде в этот момент через р2 и соответствующее показание манометра — через h2. Ясно, что p2 = р0 + h2, (16) Так как переход от состояния II к состоянию III произошел без изменения объема, то мы вправе применить здесь закон Гей-Люссака
К процессу адиабатического расширения, т. е. к переходу из состояния I в состояние II, может быть применен закон Пуассона, который удобно написать в следующей форме:
где γ — отношение удельных теплоемкостей газа при постоянном давлении и при постоянном объеме (γ=Сp/СV). Подставляя сюда значение р1 из уравнения (15) и переставляя члены, получим:
или
Так как
откуда
Следовательно, можно записать:
Откуда окончательно находим
Описание прибора. Прибор состоит (рис. 1) из стеклянного баллона А и соединенных с ним трехходового крана В и водяного манометра С. Сосуд А через кран В присоединяется к ручному воздушному насосу. 4. Практическое задание Определить показатель адиабаты с помощью лабораторной установки «Показатель адиабаты» с помощью алгоритма: 1. Кран ставят так, чтобы полость насоса соединялась только с баллоном А. Действуя насосом осторожно, нагнетают воздух в сосуд. Когда разность уровней воды в манометре достигнет 20—25 см, кран поворачивают (против стрелки часов) так, чтобы полость баллона полностью изолировалась от воздуха комнаты. 2. Подождать 2 минуты, чтобы установилось давление (температура внутри баллона выровнялась с температурой окружающей среды). После этого производят первый отсчет разности уровней в манометре h1. 3. Нажатием на клапан, расположенный сверху баллона устанавливают сообщение полости сосуда с атмосферой. Через 1с. Клапан отпускают, снова изолируя полость сосуда. 4. Подождать 2 минуты, чтобы установилось давление (температура внутри баллона выровнялась с температурой окружающей среды). После этого производят второй отсчет разности уровней в манометре h2. Опыт следует повторить не менее десяти раз, изменяя в каждом случае величину h1. Для каждой пары значений h1 и h2 по формуле (25) определяют величину отношения удельных теплоемкостей. За истинное значение принимают среднее арифметическое. Затем производят оценку погрешности измерения.
5. Контрольные вопросы 1. Сформулируйте первое начало термодинамики. 2. Дайте определение теплоемкости. Какова связь внутренней энергии с теплоемкостью при постоянном объеме? 3. Сформулируйте и докажите соотношение Майера. 4. Выведите закономерности основных изопроцессов (изотермический, изобарический, изохорный, адиабатный). Представьте полученные закономерности в виде графиков.
Лабораторная работа №6
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.237 (0.009 с.) |

 (h - расстояние, пройденное маховиком, t – время движения), может быть определено значение ускорения при движении и, в конечном итоге, момент инерции стального кольца по формуле (7).
(h - расстояние, пройденное маховиком, t – время движения), может быть определено значение ускорения при движении и, в конечном итоге, момент инерции стального кольца по формуле (7).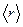 и погрешность измерения
и погрешность измерения  , в качестве которого принять дисперсию Sr (8), умноженную на коэффициент Стьюдента (определяемый из таблиц [4] для доверительной вероятности p =0.95 и количества измерений n = 10).
, в качестве которого принять дисперсию Sr (8), умноженную на коэффициент Стьюдента (определяемый из таблиц [4] для доверительной вероятности p =0.95 и количества измерений n = 10). , мм
, мм
 (8)
(8) и его дисперсию St по аналогии с (8). Также по аналогии с радиусом шкива вычислите погрешность для времени.
и его дисперсию St по аналогии с (8). Также по аналогии с радиусом шкива вычислите погрешность для времени. и погрешность его D a. Погрешность определения ускорения провести в соответствии с методикой вычисления погрешностей косвенных измерений [4].
и погрешность его D a. Погрешность определения ускорения провести в соответствии с методикой вычисления погрешностей косвенных измерений [4]. , c
, c
 вычислить момент инерции маятника Максвелла. Определить погрешность момента инерции D I, по методике определения погрешности косвенных измерений [4]. Результат представить в виде
вычислить момент инерции маятника Максвелла. Определить погрешность момента инерции D I, по методике определения погрешности косвенных измерений [4]. Результат представить в виде  .
. ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ МОЛЯРНЫХ ТЕПЛОЕМКОСТЕЙ ГАЗОВ
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ МОЛЯРНЫХ ТЕПЛОЕМКОСТЕЙ ГАЗОВ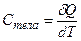 (размерность - Дж/K). Обычно пользуются молярной теплоемкостью
(размерность - Дж/K). Обычно пользуются молярной теплоемкостью 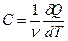 размерность – Дж/(моль К)) или удельной теплоемкостью
размерность – Дж/(моль К)) или удельной теплоемкостью  (размерность – Дж/(кг К)).
(размерность – Дж/(кг К)). или
или  . (1)
. (1) (2)
(2)
 (3)
(3) (4)
(4) (5)
(5) (6)
(6) называется законом Бойля-Мариотта.
называется законом Бойля-Мариотта. . (7)
. (7) (8)
(8) , которое известно в литературе как закон Шарля.
, которое известно в литературе как закон Шарля. (9)
(9) , а для теплоты может быть получено соотношение:
, а для теплоты может быть получено соотношение: . (10)
. (10) . (11)
. (11) (12)
(12) . (13)
. (13) .
.
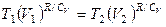 (14)
(14)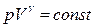
 называется показателем показатель адиабаты.
называется показателем показатель адиабаты. . (17)
. (17) (18)
(18)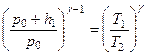 (19)
(19)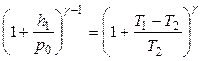 (20)
(20) и
и  - величины малые сравнительно с единицей, то, разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получим:
- величины малые сравнительно с единицей, то, разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получим: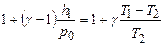 , (21)
, (21)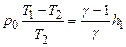 . (22)
. (22) Но выражение, стоящее в левой части уравнения, есть не что иное, как h2; действительно, подставив в уравнение (17) значение р2 из уравнения (16) и разрешив его относительно h2, получим:
Но выражение, стоящее в левой части уравнения, есть не что иное, как h2; действительно, подставив в уравнение (17) значение р2 из уравнения (16) и разрешив его относительно h2, получим: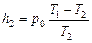 (23)
(23) , (24)
, (24) (25)
(25)


