
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 1 Определение вероятности равновероятных событийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
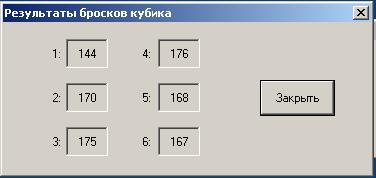
Для проведения эксперимента выбираем кнопку «Упражнение 1». Программа моделирует 1000 бросков кубика и в диалоговом окне выводит количество событий связанных с выпадением различных граней кубика 1 – 6 (рис. 5). Результаты записываются в таблицу №1. Таблица 1 Определение вероятности выпадения граней кубика
Результаты представить в виде гистограммы. Требуется убедиться в том, что вероятности выпадения граней кубика одинаковы и примерно составляют 1/6. Провести проверку условия нормировки вероятностей.
Рисунок 5 Окно выполнения упражнения 1
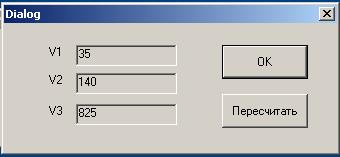
Рисунок 6 Окно выполнения упражнения 2 Упражнение 2 Блуждание частиц в замкнутом объеме Для проведения численного эксперимента выбираем в программе LabStat.exe кнопку «Упражнение 2». С помощью программы производится моделирование случайного блуждания 1000 частиц в объеме из 10000 ячеек. Программа производит 10000 итераций (случайных перемещений частиц внутри системы) и выводит на экран количество частиц попавших в каждый из элементов объема, состоящих из V1 = 400, V2 = 1600 и V3 =8900 (V3 = V - V1 - V2) ячеек. Необходимо произвести 100000 перемещений, при этом через каждые 10000 итераций определяем распределение числа частиц в системе и заносим в таблицу. Таблица 2 Вероятность попадания частицы в элемент объема
После выполнения расчетов заносим сведения в таблицу и определяем вероятность pi попадания в объем Vi. Для этого необходимо рассчитать среднее значение вероятности
где Проверьте выполнимость условия нормировки для величин
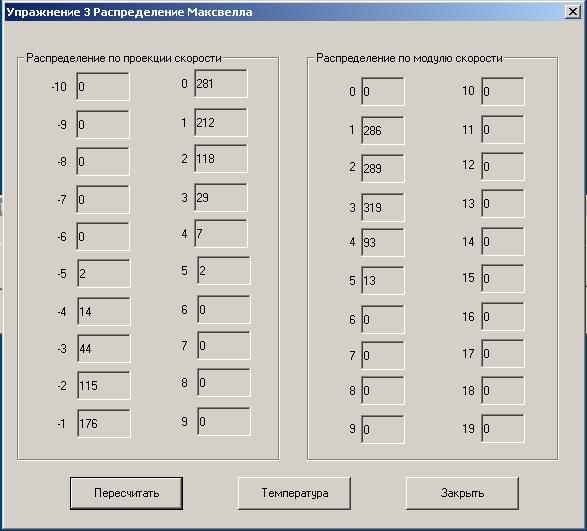
Упражнение 3 В данном упражнении проводится моделирование процесса блуждания частиц в пространстве скоростей, которое принципиально ничем не отличается от блуждания в пространстве координат. 1. Для моделирования нажмите кнопку «Упражнение 3» в программе LabStat.exe. Для осуществления расчетов распределения Максвелла (или их повтора) необходимо нажать кнопку «Пересчитать». Установить температуру, для которой осуществляется моделирование, можно нажав кнопку «Температура». Результаты расчетов выводятся в диалоговом окне, представленном на рис.7. В левой части окна представлено количество частиц имеющих различные значения проекции скорости vx. В правой части указаны количества частиц, имеющих различные значения модуля скорости v. Расчеты с помощью программы LabStat.exe необходимо провести для одной или нескольких температур, указанных преподавателем. Для каждой из температур необходимо провести не менее 3-х попыток перерасчета. Результаты перерасчета необходимо занести в табл. 3 и 4. Таблица 3 Результаты моделирования распределения по проекции скорости
Таблица 4 Результаты моделирования распределения по модулю скорости.
Рисунок 7 Окно выполнения упражнения 3
2. С помощью результатов, полученных при обработке расчетных данных (табл.3 и 4), необходимо построить гистограммы распределения вероятностей в зависимости от значения проекции скорости vx и модуля скорости v для рассмотренных температур. 3. С помощью результатов, полученных при обработке расчетных данных (табл.3 и 4), необходимо построить графики зависимостей 4. Если расчеты проводились для нескольких температур, то необходимо сделать выводы относительно изменения распределений в зависимости от температуры и убедиться в линейности поведения дисперсии от температуры. 4. Контрольные вопросы 1. Дайте определение понятий: вероятность, распределение вероятности и плотность вероятности? В чем состоит условие нормировки? 2. Получите на примере физической системы биноминальное распределение. Вычислите среднее значение и среднеквадратичное отклонение для биноминального распределения. 3. Докажите, что средняя кинетическая энергия молекул идеального газа не зависит от массы молекул. 4. Получите на примере физической системы распределение Максвелла по проекциям и модулю скорости. Вычислите среднее квадратичное значение модуля скорости. 5. Что характеризуют среднеквадратичное значение скорости и наиболее вероятная скорость движения частиц идеального газа?
Погрешности результатов измерений физических величин 1. Основные определения. Прямыми измерениями называют такие измерения, при которых с помощью эталонного прибора измеряют непосредственно исследуемую величину X (например, прямым измерением является измерение длины при помощи линейки). Косвенными измерениями называют такие измерения, при которых искомое значение величины находится на основании известной зависимости между этой величиной и величинами, определяемыми прямыми измерениями (например, косвенным измерением является измерение плотности тела по результатам прямых измерений его массы и объема). Абсолютная погрешность DX измерения – это разность между измеренным (Xизм) и истинным значением (Xист) измеряемой величины:
Относительная погрешность измерения d равна отношению абсолютной погрешности измерения к истинному значению измеряемой величины:
Истинное значение измеряемой величины Xист экспериментатору не известно. Наиболее близко к истинному значению лежит среднее значение измеряемой величины, определяемой по формуле
где Xi – значение измеряемой величины в i -ом измерении, n – число измерений. Оценку абсолютной погрешности i -го измерения можно найти по формуле
Систематическая погрешность измерения – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при измерениях. Она может быть вызвана неточностью метода измерения, погрешностями приборов и другими причинами. Случайная погрешность измерения – это составляющая погрешности измерения, изменяющаяся случайным образом (даже при повторных прямых измерениях).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.19 (0.005 с.) |


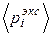

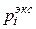
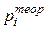
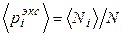 , среднеквадратичное отклонение
, среднеквадратичное отклонение 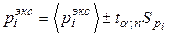 ,
, - коэффициент Стьюдента для доверительной вероятности a=0,95 и n =10.
- коэффициент Стьюдента для доверительной вероятности a=0,95 и n =10.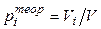 .
.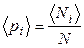
 , отн.ед.
, отн.ед.
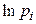
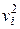 , отн.ед.
, отн.ед.
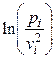 , отн.ед.
, отн.ед.
 от
от  и
и 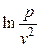 от
от 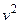 . Линейность этих зависимостей позволяет подтвердить справедливость распределения Максвелла для рассмотренной системы. Сравните между собой коэффициенты наклона для этих двух линейных зависимостей.
. Линейность этих зависимостей позволяет подтвердить справедливость распределения Максвелла для рассмотренной системы. Сравните между собой коэффициенты наклона для этих двух линейных зависимостей.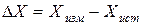 (1)
(1)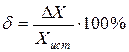 (2)
(2)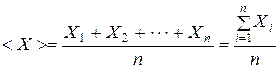 , (3)
, (3)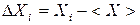 (4)
(4)


