
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По основам механики и молекулярной физикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ФИЗИКА Сборник лабораторных работ По основам механики и молекулярной физики для студентов инженерных специальностей
Ульяновск, 2009 год УДК 531 + 539.19 (075.8) ББК 22.2я73 + 22.36 я73 Ф 50
Печатается по решению Ученого совета Инженерно-физического факультета высоких технологий
Рецензенты: Журавлев В.М. – доктор физико-математических наук, профессор кафедры теоретической физики Ульяновского государственного университета Самохвалов М.К. – доктор физико-математических наук, зав. кафедрой Ульяновского государственного технического университета
СОДЕРЖАНИЕ Механика
Молекулярная физика
ИЗУЧЕНИЕ ЗАКОНОВ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ Цель работы: изучение динамики поступательного движения связанной системы тел с учетом силы трения; оценка роли трения как источника систематической погрешности при определении ускорения свободного падения на лабораторной установке. Приборы и принадлежности: установка «машина Атвуда», набор грузов (массу грузов и погрешность определения масс грузов уточнить у инженера), электронный секундомер (входит в состав установки). Материал для изучения: Уравнения динамики поступательного движения; сила трения; определение погрешностей измерений.
1. Основные понятия и определения Материальная точка – тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь.
Система координат – совокупность тела отсчета и осей координат, позволяющих определять положение тел друг относительно тела отсчета (в простейшем случае декартова прямоугольная система координат – рис.1).
Уравнение движения материальной точки – уравнение, выражающее зависимость радиус-вектора материальной точки (или ее координат) от времени:
Приращение радиус-вектора (вектор перемещения) – это вектор Путь – длина участка траектории, пройденного материальной точкой, за данный промежуток времени.
Скорость – векторная величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Средняя скорость
Направление вектора средней скорости совпадает с направлением Модуль средней скорости:
Мгновенная скорость
Модуль мгновенной скорости:
Ускорение – характеристика неравномерного движения; определяет быстроту изменения скорости по модулю и направлению. Среднее ускорение
Мгновенное ускорение
Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории):
Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории):
где r – радиус кривизны траектории в данной точке. Полное ускорение при криволинейном движении – геометрическая сумма тангенциальной и нормальной составляющих (рис. 4):
Теоретическое введение Рассмотрим задачу о движении тела массы m в поле тяжести. В соответствии со вторым законом Ньютона уравнение движения тела может быть записано в виде:
Так как сила тяжести, действующая на тело, прямо пропорциональна его массе Ускорение по определению может быть связано с вектором скорости
Скорость может быть представлена в виде производной от радиус-вектора: Теперь может быть определена зависимость радиус-вектора от времени:
Окончательное выражение для зависимости радиус-вектора от времени имеет вид:
Рисунок 5. Траектория движения тела в поле тяжести.
Рассмотрим зависимость координат Предположим (см. рис.5), что в начальный момент времени частица находилась в начале координат (x 0=0, y 0=0), а ускорение направлено в сторону противоположную оси OY (
Если выразить время
Очевидно, что в соответствии с формулой (3), траектория движения тела в поле тяжести описывается параболой (см. рис. 5). Одним из частных случаев движения в поле тяжести является падение тела с высоты h без начальной скорости v 0=0. Подстановка таких начальных условий в общее уравнение (1) приводит к следующей зависимости координат x и y от времени:
Вторая формула в выражении (4) позволяет связать время падения t тела с высоты h и ускорение свободного падения: h = g t 2/2. (5) Особенности определения ускорения свободного падения Непосредственное измерение ускорения свободного падения с помощью формулы (5) произвести достаточно сложно. Если тело падает с высоты h = 1,0 м, то при g = 9,8 м/с2, время падения составит менее 0,5с.
Таким образом, точное определение ускорения свободного падения требует точного определения времени падения (по крайней мере, с точностью до 0,01с). Если увеличить высоту, то время падения тоже увеличится. Так, при h = 5 м время падения будет 1с, а при h = 20 м – 2 с. В этом случае можно ограничиться меньшей точностью при измерении времени, например 0,01 c, но возникает ошибка другого характера. Сопротивление воздуха при больших скоростях играет заметную роль. Если считать, что на тело действует и сила тяжести, и сила трения о воздух, то уравнение движения будет иметь вид:
Сила трения о воздух в первом приближении может быть связана со скоростью Очевидно, что чем больше сила тяжести будет увеличивать скорость, тем больше будет сила трения. В конечном итоге сила трения и сила тяжести уравновесят друг друга, а само движение станет равномерным. Если ma = 0, то
или для предельного значения скорости соответствующей скорости Таким образом, наличие силы трения делает невозможным точное определение ускорения свободного падения g, путем наблюдения их свободного падения в поле тяжести. Машина Атвуда
1) блок и нить невесомы, т. е. их массы равны нулю; 2) С учетом этих предположений уравнения движения грузов имеют вид
где T – сила натяжения нитей, a – ускорение грузов. Из уравнений (7) получаем
где Время, за которое груз опускается на высоту h, равно
Формально из выражения (9) следует, что время падения груза может быть сколь угодно большим, если уменьшить e. Например, если взять грузы массами М = 5 кг каждый, перегрузок массой m = 1 г, то e = 10-4, а время спуска груза на высоту h = 1 м примерно равно 45 с. Это время можно достаточно точно измерить секундомером. Однако реально такой опыт невыполним. Мы, предположили, что трение в оси блока отсутствует. Но в действительности оно есть. Весь вопрос в том, можно ли им пренебречь или нет. Если подвести к блоку на нитях тяжелые грузы, то в оси блока будет большая сила трения. Чем массивнее грузы, тем больше сила трения. Значит, необходимо брать достаточно тяжелый перегрузок, чтобы преодолеть эту силу трения и привести всю систему в движение. Сделаем теперь количественные оценки. Пусть m0 – масса такого перегрузка, который только-только страгивает блок с грузами. Это значит, что любой перегрузок меньшей массы не приводит систему в движение. В этом случае момент сил натяжения нитей равен моменту силы трения Мтр в оси блока:
где T2 = (M+m0) ×g и T1 = M×g – силы натяжения нитей, R – радиус блока (рис.7).
Сила трения Fтр между блоком и осью пропорциональна силе давления на оси блока. Тогда
где m – коэффициент трения между блоком и осью, зависящий от свойств соприкасающихся поверхностей втулки блока и оси, смазки и т.п. Таким образом, момент силы трения в оси блока
Обозначим
Как видно из (12), значение e0 не может быть сколь угодно малым, Оно определяется конструкцией блока (например, его радиусами R и r) и коэффициентом трения между блоком и осью. Так как в машине Атвуда m0 << M, то e0 << 1 и
Какое же значение e0 можно ожидать? Типичное значение коэффициента трения m ~ 10-2 ¸ 10-1. На наших установках r/R ~10-2 ¸ 10-1. Таким образом, e0 ~ 10-4 ¸ 10-2. Мы привели лишь правдоподобные рассуждения о том, каким может быть e0. Существенно то, что e0 можно оценить экспериментально. Например, на установке с грузами массой M = 86г перегрузок массой 1г не страгивает блока, а перегрузок массой 2 г приводит блок в движение. Это значит, что
В таком случае оценить e0, характеризующую установку, можно лишь по порядку величины. Как оказывается, она порядка 10-2. Интуитивно ясно, что трением можно пренебречь, если масса перегрузка m>>m0. Действительно, если масса перегрузка чуть больше m0, то трение в оси блока будет решающим образом определять движение грузов. Это движение уже не будет равноускоренным. Может даже случиться, что система будет двигаться рывками, т.е. остановится, затем снова придет в движение и т.д. Таким образом, при m~m 0, т.е. при e~e 0, формула (8) становится неверной. Можно ожидать, что при Можно показать (смотри контрольный вопрос 9), что относительная погрешность при определении ускорения грузов, связанная с пренебрежением массой блока и трением, равна
где mб – масса блока. Так как величины m0/m и mб/(2М) одного и того же порядка 10-1, то и относительная погрешность при измерении ускорении D a /< a >~ 0,1. Очевидно, что такого же порядка будет и относительная погрешность при измерении g. Методика измерений Экспериментальная установка «машина Атвуда» представлена на рис.8. Блок B крепится наверху вертикальной стойки A, на которой нанесена шкала. Если на груз C массы M положить перегрузок D массой m, то система начнет двигаться с некоторым ускорением a. Увеличивая массу перегрузка m, можно увеличивать ускорение системы a. Если после того, как груз C с перегрузком D прошел некоторое расстояние S1, перегрузок D снять с груза C, то последний будет продолжать движение с постоянной скоростью, равной по величине скорости груза в момент снятия перегрузка. Для реализации такой ситуации на стержне A установки делаются три кронштейна: нижний E – неподвижный, средний, с кольцевой платформой – F и верхний G – подвижные, которые можно перемещать вдоль стойки и фиксировать в любом положении, устанавливая таким образом длину пути равномерно ускоренного и равномерного движений. Все кронштейны имеют указатели положения. На среднем кронштейне кроме кольцевой платформы закреплен фотоэлектрический датчик. В тот момент, когда кольцевая платформа снимает с большого груза C перегрузок D, фотоэлектрический датчик образует электрический импульс, сигнализирующий о начале равномерного движения больших грузов C и C’. Оптическая ось фотодатчика находится на уровне указателя положения среднего кронштейна. Нижний кронштейн оснащен двумя платформами с резиновыми амортизаторами, в которые ударяются завершающие свое движение грузики, а также фотодатчиком с оптической осью на уровне указателя положения кронштейна. Фотоэлектрический датчик вырабатывает импульс напряжения, сигнализирующий о конце равномерного движения. Система грузов может удерживаться в состоянии покоя с помощью специальной фрикционной муфты, перемещающейся с помощью электромагнита. Для измерения времени t равномерного движения и управления фрикционной муфтой прибор имеет электронный блок K, в состав которого входят таймер и система управления электромагнитом. Включение электронного блока осуществляется нажатием клавиши «сеть». При нажатии на клавишу «сброс» происходит обнуление табло таймера. В исходном состоянии система заторможена посредством фрикционной муфты. Груз C устанавливают в исходное положение: его нижняя грань должна быть на уровне горизонтальной черты на верхнем кронштейне G. При нажатии на клавишу «пуск» происходит освобождение системы (разрывается цепь электромагнита) и генерируется импульс, дающий разрешение на включение таймера от импульса, который будет выработан фотодатчиком на среднем кронштейне F в момент снятия с груза C перегрузка D. Импульс от нижнего электрического датчика останавливает работу таймера; результат высвечивается на табло. При этом снова замыкается цепь электромагнита, и система затормаживается фрикционной муфтой. Машина Атвуда позволяет проверить законы равноускоренного движения и второй закон Ньютона. Пусть грузы C и C’ проходят равноускоренно путь S 1 (от кронштейна G до кронштейна F), с ускорением a, в течение времени t, тогда
а скорость в конце пути будет
Тогда, если тела C и C’ проходят затем равномерно (со скоростью V) путь S 2 (от кронштейна F до кронштейна E) за время t, то
Из выражений (14)-(15) можно получить следующее соотношение:
Из (8) и (17) следует, что если величина массы перегрузка m постоянна, то величина ускорения a системы будет также неизменна при любых комбинациях величин S 1 и S 2. Проверке этого утверждения и определения величины a для заданного перегрузка и составляет содержание первого упражнения. Для заданного перегрузка m и ряда различных значений S 1 и S 2 измеряется время t прохождения грузом участка S 2. Измерения времени прохождения участка S 2 для каждой комбинации производятся несколько раз, результаты усредняются и записываются в виде
где
Поэтому было бы грубой ошибкой считать, что погрешность определения времени падения равна 10-3 с. Во втором упражнении исследуется зависимость времени прохождения участка S2 от массы перегрузка. Для этого устанавливаются фиксированные значения S1 и S2 и определяется значение ускорений a для различных значений массы перегрузка m. Для каждого перегрузка время t определяется несколько раз, затем результаты усредняются. Подстановка формулы (8) в (17) приводит к выражению:
В осях координат Измерение времени падения при каждом m повторяют несколько раз, результаты усредняют и находят среднее значение Прежде чем приступать к выполнению упражнений, необходимо в первую очередь определить минимальную массу перегрузка m0, страгивающего блок, с тем, чтобы в дальнейшем проводить измерения с грузами, в 5–10 раз превышающими по массе m0. Только в этом случае можно пренебречь влиянием трения на движение системы. Не следует стремиться определить m0 точно, достаточно получить ее правильную оценку «сверху», например выяснить, что m0 не превышает 1г или 2г. Для определения m0 можно постепенно увеличивать массу перегрузка, пока блок не придет в движение. Так как блок не может быть отцентрирован идеально, то может оказаться, что в различных начальных положениях блока массы страгивающего перегрузка различны. Поэтому нужно повторить измерения m0 в разных положениях блока, а затем в качестве оценки для m0 взять наибольшее из найденных значений.
4. Практическое задание 1. Определите массу m0 перегрузка, обеспечивающего начало движения. Для этого, постепенно увеличивая массу m перегрузка, определите с точностью до 0,5 г значение m0, начиная с которого блок приходит в движение. Измерения повторите при четырех положениях блока, каждый раз поворачивая блок примерно на 90° по отношению к предыдущему положению. В качестве m0 следует принять наибольшее из найденных значений. 2. Определите экспериментально время t прохождения грузом C участка S2. Измерения проведите при определенном выбранном значении массы перегрузка m = (5¸10) m0. При этом необходимо также, чтобы выполнялось неравенство
Определите время t для пяти комбинаций S 1 и S 2, повторяя измерения времени t для каждых значений S1 и S2 по четыре раза. Результаты занесите в табл.1. Таблица 1
Здесь t1,..., t4 –результаты измерения времени прохождения участка S 2:
где ap,n=3.2 – коэффициент Стьюдента для доверительной вероятности p=0,95 и количества измерений n = 4. Для каждой комбинации определите среднее значение 3. Определите опытным путем зависимость времени прохождения участка S 2 от массы m перегрузка. Измерения проводите при фиксированной комбинации S 1 и S 2 для пяти значений массы m. Для каждого значения m повторите измерения четыре раза, результаты занесите в табл.2. Таблица 2
Все значения массы m перегрузка должны лежать в диапазоне
По результатам измерений в осях координат По наклону прямой с помощью соотношения (18) определите ускорение свободного падения g и погрешность D g по методу наименьших квадратов (см. учебно-методическое пособие [4]). Контрольные вопросы 1. Что такое материальная точка? 2. Что такое тело отсчета, система координат, система отсчета? 3. Что такое радиус-вектор материальной точки, уравнения движения материальной точки? 4. Дайте определения траектории, перемещения и пути. 5. 6. Как направлены векторы скорости и полного ускорения относительно траектории движения? 7. Почему измеренное ускорение свободного падения меньше, а не больше, чем 9,8 м/с2? 8. Какова относительная погрешность измерения g? 9. Блок представляет собой тонкий обруч массой mб с невесомыми спицами и втулкой (рис.10). Радиус обруча R, радиус втулки r. Втулка насажена на ось. Коэффициент трения между втулкой и осью m. Через блок перекинута нить, на которой укреплены грузы массой М и перегрузок массой m. Определите ускорение а системы и относительную погрешность Лабораторная работа № 2
Цель работы: изучение законов динамики вращательного движения, проверка теоремы Гюйгенса-Штайнера, оценка влияния трения на точность результатов проведенных измерений.
Приборы и принадлежности: Лабораторная установка «маятник Обербека», набор грузов (массы грузов и погрешности их определения указаны на грузах), электронный секундомер (в составе установки).
Материал для изучения: Уравнение динамики вращательного движения. Момент инерции. Сила трения. Оценка погрешностей измерений.
1. Основные понятия и определения Абсолютно твердое тело – тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (точнее между двумя частицами) этого тела остается постоянным. Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука, а после прекращения действия внешних сил принимает свои первоначальные размеры и форму. Абсолютно неупругое тело – тело, полностью сохраняющее деформированное состояние после прекращения действия внешних сил.
Вращательным движением твердого тела называется движение, связанное с движением точек тела по окружностям. Прямая, проходящая через центры окружностей, называется осью вращения. Вращательное движение как материальной точи, так и твердого тела может быть охарактеризовано вектором угловой скорости и вектором углового ускорения.
Скорость движения материальной точки при вращательном движении определяется с помощью векторного произведения векторов угловой скорости и радиус-вектора (см. рис.1):
Напомним, что векторным произведением называется правило, в соответствии с которым двум векторам Вектор углового ускорения определяется как производная угловой скорости по времени: Основными понятиями динамики вращательного движения являются момент импульса Момент импульса и момент силы являются аддитивными величинами. Для вычисления момента импульса системы, состоящей из нескольких частиц (тел), необходимо вычислить сумму моментов импульса соответствующих каждой из частиц: Основное уравнение динамики вращательного движения является следствием законов Ньютона и формулируется в виде соотношения:
В случае, если взаимодействие между частицами (телами) системы осуществляется с помощью центральных сил, то полный момент сил, действующих в системе определяется только внешними силами: Рассмотрим однородное симметричное твердое тело, вращающееся вокруг оси симметрии. У такого тела ось симметрии (следовательно и ось вращения) проходят через центр масс. Моментом инерции твердого тела называется мера инертности твердого тела при его вращательном движении. Если направить ось z вдоль оси вращения (рис.2.), то можно доказать, что
При этом момент инерции относительно оси z может быть вычислен с помощью формулы где Ri - расстояние от элемента тела массой mi до оси z. Соответственно уравнение динамики вращательного движения твердого тела (1) запишется в виде:
или
Рисунок 2. В общем случае (неоднородное распределение массы, произвольная ось вращения) векторы
Вместо одной велич
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 838; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.234 (0.014 с.) |

 Лабораторная работа № 1
Лабораторная работа № 1 Тело отсчета – произвольно выбранное тело, относительно которого определяется положение других (движущихся) тел.
Тело отсчета – произвольно выбранное тело, относительно которого определяется положение других (движущихся) тел. или
или 
 Траектория – линия, описываемая движущейся материальной точкой (или телом), относительно выбранной системы отсчета.
Траектория – линия, описываемая движущейся материальной точкой (или телом), относительно выбранной системы отсчета. (рис.2).
(рис.2). – векторная величина, определяемая отношением приращения радиуса-вектора точки
– векторная величина, определяемая отношением приращения радиуса-вектора точки  к промежутку времени Dt:
к промежутку времени Dt: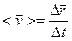
 .
.
 – векторная величина, определяемая первой производной радиус-вектора движущейся точки по времени:
– векторная величина, определяемая первой производной радиус-вектора движущейся точки по времени: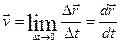
 Вектор мгновенной скорости направлен по касательной к траектории в сторону движения (рис. 3).
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения (рис. 3).
 – векторная величина, равная отношению изменения скорости
– векторная величина, равная отношению изменения скорости  к интервалу времени D t:
к интервалу времени D t:
 – векторная величина, определяемая первой производной скорости по времени:
– векторная величина, определяемая первой производной скорости по времени:


 ,
,

 , то движение происходит с постоянным ускорением независимо от свойств тела:
, то движение происходит с постоянным ускорением независимо от свойств тела:  .
. . Тогда для скорости может быть записано
. Тогда для скорости может быть записано  , которое легко интегрируется:
, которое легко интегрируется:
 - скорость в начальный момент времени. Таким образом, вектор скорости линейно зависит от времени:
- скорость в начальный момент времени. Таким образом, вектор скорости линейно зависит от времени:

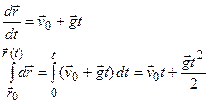
 (1)
(1)
 и
и  тела движущегося в поле тяжести.
тела движущегося в поле тяжести. ). Из формулы (1) следует, что координаты имеют следующую зависимость от времени:
). Из формулы (1) следует, что координаты имеют следующую зависимость от времени: (2)
(2) и подставить в уравнение для зависимости y (t), то можно получить вид траектории, которую описывает тело при движении в поле тяжести:
и подставить в уравнение для зависимости y (t), то можно получить вид траектории, которую описывает тело при движении в поле тяжести: . (3)
. (3) (4)
(4)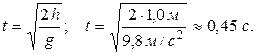
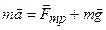 (6)
(6)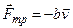 (b – постоянная величина, которая зависит от формы тела и свойств среды, в которой происходит движение).
(b – постоянная величина, которая зависит от формы тела и свойств среды, в которой происходит движение).
 .
. Избежать перечисленных проблем, можно с помощью устройства, которое называют машиной Атвуда (рис.6). Через блок перекинута нить, на которой закреплены грузы массой M каждый. На один из: грузов кладется перегрузок массой m. Ускорение грузов легко найти, если ввести два предположения:
Избежать перечисленных проблем, можно с помощью устройства, которое называют машиной Атвуда (рис.6). Через блок перекинута нить, на которой закреплены грузы массой M каждый. На один из: грузов кладется перегрузок массой m. Ускорение грузов легко найти, если ввести два предположения: трение тела о воздух и трением между блоком и его осью можно пренебречь.
трение тела о воздух и трением между блоком и его осью можно пренебречь. (7)
(7)
 .
.
 (10)
(10) Момент силы трения в оси блока Mтр = Fтр×r, где Fтр – сила трения между блоком и осью, r – радиус оси.
Момент силы трения в оси блока Mтр = Fтр×r, где Fтр – сила трения между блоком и осью, r – радиус оси.
 (11)
(11) . Подставим (11) в (10):
. Подставим (11) в (10): (12)
(12)

 она достаточно точно описывает реальную ситуацию. Так как
она достаточно точно описывает реальную ситуацию. Так как  , то оптимальное значение e ~10-1. Это значит, что экспериментировать надо с перегрузками 5–20 г (при М = 86 г). Если взять e ~ 1, то а ~ g. Мы приходим к случаю почти свободного падения.
, то оптимальное значение e ~10-1. Это значит, что экспериментировать надо с перегрузками 5–20 г (при М = 86 г). Если взять e ~ 1, то а ~ g. Мы приходим к случаю почти свободного падения.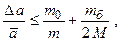

 (15)
(15) (16)
(16)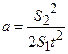 (17)
(17)
 – среднее арифметическое значение измеренного времени падения для данной высоты. В условиях эксперимента погрешность D t оказывается заметно превышающей погрешность в показаниях электронного миллисекундомера (D t)0, а именно:
– среднее арифметическое значение измеренного времени падения для данной высоты. В условиях эксперимента погрешность D t оказывается заметно превышающей погрешность в показаниях электронного миллисекундомера (D t)0, а именно:
 (18)
(18) функция
функция 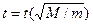 является уравнением прямой. Зависимость
является уравнением прямой. Зависимость  , затем через полученные точки проводится прямая, по наклону которой определяется значение g.
, затем через полученные точки проводится прямая, по наклону которой определяется значение g.
 , c
, c
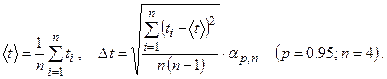
 по всем комбинациям.
по всем комбинациям.

 В нашей лабораторной установке точность D m определения массы по существу совпадает со значением массы m0 перегрузка.
В нашей лабораторной установке точность D m определения массы по существу совпадает со значением массы m0 перегрузка. Дайте определения следующих физических величин: средняя скорость, мгновенная скорость, среднее ускорение, мгновенное ускорение, нормальная и тангенциальные составляющие ускорения, полное ускорение.
Дайте определения следующих физических величин: средняя скорость, мгновенная скорость, среднее ускорение, мгновенное ускорение, нормальная и тангенциальные составляющие ускорения, полное ускорение. , связанную с пренебрежением трением и массой блока.
, связанную с пренебрежением трением и массой блока. ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ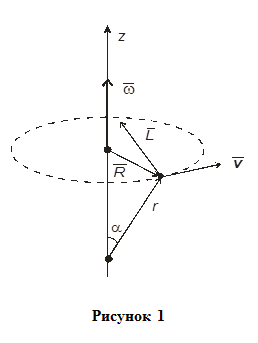 Вектором угловой скорости (рис. 1) называется вектор
Вектором угловой скорости (рис. 1) называется вектор  численно равный скорости изменения угла j и направленный перпендикулярно плоскости вращения в соответствии с правилом правого винта:
численно равный скорости изменения угла j и направленный перпендикулярно плоскости вращения в соответствии с правилом правого винта:  . Отметим, что такое представление о векторе угловой скорости дает возможность анализировать одновременное вращение вокруг нескольких осей, при этом вектор угловой скорости будет равен сумме векторов угловой скорости, связанных с вращением вокруг каждой из осей.
. Отметим, что такое представление о векторе угловой скорости дает возможность анализировать одновременное вращение вокруг нескольких осей, при этом вектор угловой скорости будет равен сумме векторов угловой скорости, связанных с вращением вокруг каждой из осей.
 и
и  , ставится в соответствие вектор
, ставится в соответствие вектор  , а направление вектора определяется по правилу правого винта.
, а направление вектора определяется по правилу правого винта. .
. и момент силы
и момент силы  . Моментом импульса называется величина равная векторному произведению радиус-вектора
. Моментом импульса называется величина равная векторному произведению радиус-вектора  и вектора импульса
и вектора импульса  :
:  . Моментом силы называется величина равная векторному произведению радиус-вектора
. Моментом силы называется величина равная векторному произведению радиус-вектора  :
:  .
. . Аналогично для момента силы:
. Аналогично для момента силы:  .
. (1)
(1) .
. ,
,  ,
,  .
. ,
,
 (1a)
(1a)
 и
и 



