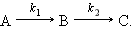Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типы простых мономолекулярных и бимолекулярных реакцийСодержание книги
Поиск на нашем сайте
Тримолекулярные реакции характерны для каталитических и ингибированных процессов, а также процессов, протекающих с выделением значительного количества энергии, когда стабилизация образовавшейся в ходе бимолекулярной химической реакции молекулы достигается путем передачи энергии третьей частице. Число молекул, вступающих в реакцию, определяют молекулярность реакции. Так, если в реакцию вступает одна молекула, то такая реакция называется молекулярной реакцией. Если в реакции участвуют две молекулы (безразлично, одинаковые или нет), то такая реакция называется бимолекулярной. Встречаются также тримолекулярные реакции. Реакции более высокой степени молекулярности крайне редки из–за малой вероятности одновременного столкновения большого числа молекул. Поэтому большинство реакций протекают в несколько элементарных, простых стадий, в которых участвует небольшое число молекул. Определить такие стадии – значит определить механизм, или путь реакции. Скорость всей реакции определяется скоростью её наиболее медленной стадии, которая и определяет механизм. Поэтому закон действующих масс справедлив только для таких элементарных стадий. Молекулярность реакции легко определить в случае простых реакций, протекающих в одну стадию. В большинстве же случаев довольно трудно найти молекулярность реакции. Поэтому вводится понятие порядка реакции, который можно найти из кинетических уравнений, полученных экспериментально. Порядок реакции по данному веществу равен степени, в которой концентрация данного вещества входит в уравнение скорости реакции. Сумма показателей степеней, в которых концентрация всех исходных веществ входит уравнение скорости реакции, равна порядку реакции в целом. Порядок химической реакции по веществу совпадает со стехиометрическим коэффициентом реакции лишь в очень простых реакциях, например в реакции синтеза йодистого водорода:
H2 + I2 ® 2HI.
Порядок этой реакции по водороду (первый) и йоду (первый) равны стехиометрическими коэффициентами, а общий порядок реакции (второй) равен сумме стехиометрических коэффициентов в уравнении скорости реакции В подавляющем большинстве случаев порядок реакции по веществу отличается от стехиометрических коэффициентов уравнения реакции для этого вещества. Соответственно общий порядок реакции обычно не равен сумме стехиометрических коэффициентов уравнения реакции. Уравнение, выражающее зависимость скорости реакции от концентрации каждого вещества, называют кинетическим уравнением реакции в дифференциальной форме. К сожалению, кинетическое уравнение реакции может быть получено только при её экспериментальном изучении и не может быть выведено из стехиометрического уравнения.
18. Кинетика односторонних реакций простых типов, протекающих в статических условиях. Реакции первого порядка. Для простой реакции молекулярность – это число частиц, принимающих участие в элементарном акте химического взаимодействия. В данном случае порядок и молекулярность совпадают. Простые реакции могут быть мономолекулярными, бимолекулярными, тримолекулярными. Участие в элементарном акте более трех частиц маловероятно. односторонние реакции первого порядка Согласно закону действующих масс кинетическое уравнение для односторонней мономолекулярной реакции первого порядка
Константа скорости реакции первого порядка имеет размерность (время)-1, например, с-1, мин-1, ч-1, поэтому ее числовое значение зависит от единиц, в которых выражается время. Для характеристики скорости реакции, наряду с константой скорости, часто пользуются временем полупревращения или полураспада (t1/2), равным промежутку времени, в течение которого реагирует половина взятого количества вещества. Например, из уравнения (11), при
Уравнение первого порядка описывает не только скорость элементарных мономолекулярных реакций. Многие сложные реакции подчиняются уравнению первого порядка. Например, зависимость скорости реакции гидролиза этилацетата в водной среде:
от концентрации описывается уравнениями первого порядка. Для указанной реакции это обусловлено тем, что концентрация воды, находящейся в избытке, в ходе реакции остается практически постоянной, поэтому ее можно ввести в константу скорости
где Такие реакции называются псевдомономолекулярными. Определенное интегрирование уравнения (11) позволяет получить уравнение в интегральной форме:
из которого следует
где С0 - начальная концентрация исходного вещества А, отвечающая моменту времени, равному нулю; С - концентрация этого вещества к моменту времениt. При кинетическом изучении реакции первого порядка вместо концентраций можно использовать любые другие величины, которые меняются пропорционально концентрации, так как в уравнение (14) входит отношение концентраций. Если в это уравнение подставить вместо концентрации пропорциональную ей величину, то коэффициент пропорциональности сократится и величина под логарифмом не изменится. Например, концентрации можно заменить через количество исходного вещества в системе
где а=C0V - начальное количество вещества в молях; а-х=CV - количество вещества, которое осталось во всем объеме V системы к моменту времениt, в молях; х - количество прореагировавшего вещества, в молях. Из уравнения (15) можно определить количество прореагировавшего вещества:
а также количество непрореагировавшего вещества к моменту времени t:
По первому порядку протекают многие реакции разложения и изомеризации. Реакции нулевого порядка Для реакций нулевого порядка кинетическое уравнение имеет следующий вид:
Скорость реакции нулевого порядка постоянна во времени и не зависит от концентраций реагирующих веществ; это характерно для многих гетерогенных (идущих на поверхности раздела фаз) реакций в том случае, когда скорость диффузии реагентов к поверхности меньше скорости их химического превращения. Реакции первого порядка Рассмотрим зависимость от времени концентрации исходного вещества А для случая реакции первого порядка А ––> В. Реакции первого порядка характеризуются кинетическим уравнением вида (II.6). Подставим в него выражение (II.2):
После интегрирования выражения (II.7) получаем:
Константу интегрирования g определим из начальных условий: в момент времени t = 0 концентрация С равна начальной концентрации Со. Отсюда следует, что g = ln Со. Получаем:
Рис. 2.3 Зависимость логарифма концентрации от времени для реакций Т.о., логарифм концентрации для реакции первого порядка линейно зависит от времени (рис. 2.3) и константа скорости численно равна тангенсу угла наклона прямой к оси времени.
Из уравнения (II.9) легко получить выражение для константы скорости односторонней реакции первого порядка:
Еще одной кинетической характеристикой реакции является период полупревращения t1/2 – время, за которое концентрация исходного вещества уменьшается вдвое по сравнению с исходной. Выразим t1/2 для реакции первого порядка, учитывая, что С = ½Со:
Отсюда
Как видно из полученного выражения, период полупревращения реакции первого порядка не зависит от начальной концентрации исходного вещества.
19. Реакции второго порядка. Реакции третьего порядка. Определение порядка реакции. Кинетическое уравнение реакции второго порядка:
Если
Для реакций второго порядка время полупревращения и константа скорости реакции обратно пропорциональны начальной концентрации исходного вещества С0. Уравнение будет несколько сложнее для реакции между веществами, концентрации которых неодинаковы ( А+В→Р (V=const) Исходное количество молей (=0) Через время (сек) Концентрация через (сек) Окончательно получим: ()
ЕАКЦИИ ТРЕТЬЕГО ПОРЯДКА (n=3). Эти реакции встречаются очень редко. Примерами могут служить реакции: 2NO+O2 → 2NO2; 2CO+O2 → 2CO2 Основное кинетическое уравнение для реакции третьего порядка имеет вид:
Если
Время полупревращения и константа скорости реакции третьего порядка обратно пропорциональны квадрату начальной концентрации вещества. Для любого n-го порядка время полупревращения можно выразить по формуле:
Для каждого порядка реакции существует своя собственная зависимость концентрации от времени. Так как молекулярность и порядок реакции в большинстве случаев не совпадают, то для проведения кинетического анализа химического процесса необходимо верно определить порядок реакции. Зная порядок реакции, используют кинетические уравнения для расчета констант скорости при различных температурах, затем рассчитывают энергию активации реакции и другие кинетические характеристики. Определение порядка химической реакции основывается на экспериментальных данных об изменении концентрации реагирующих веществ с течением времени при постоянной температуре. При этом используются либо начальные участки серии кинетических кривых, либо одна более полная кинетическая кривая. Существуют различные способы определения порядка реакции, предполагающие использование одного из следующих двух подходов: 1. метод равных концентраций; 2. метод избытка Оствальда. Метод равных концентраций применяют при определении порядка реакции в целом. Метод избытка Оствальда (метод изоляции) используют при определении порядка реакции по каждому из реагентов. По этому методу проводят серии опытов, в каждом из которых изучается влияние концентрации только одного из исходных веществ на скорость реакции. Для этого все остальные исходные вещества берутся в таком избытке, чтобы их концентрации в ходе реакции можно было считать постоянными. Это позволяет упростить кинетическое уравнение и определить порядок реакции по одному из исходных реагентов. Сумма порядков реакции по всем исходным веществам представляет собой порядок реакции в целом. Таким образом, и первый и второй подход предполагают определение показателей степеней кинетического уравнения вида
Различают две группы методов определения порядков реакции: интегральные и дифференциальные. К группе интегральных методов определения порядков реакции относятся все методы, основанные на использовании интегральных форм кинетических уравнений соответствующих порядков: метод подстановки, графический метод, по периоду полупревращения, способ Оствальда-Нойеса. Метод подстановки. Заключается в подстановке экспериментальных значений концентраций реагирующего вещества, соответствующих определенным промежуткам времени от начала реакции, в кинетические уравнения различных порядков (14, 16, 21, 22, 25, 28, 31) и установление такого уравнения, которое дает постоянное значение константы скорости. Графический метод. Зависимость концентрации от времени для реакций различных порядков может быть выражена прямой линией, если выбрать соответствующую систему координат. Так, для реакции первого порядка прямая получается в системе координат Метод подбора кинетического уравнения заключается в подстановке экспериментальных данных изучения зависимости концентрации вещества от времени в кинетические уравнения различных порядков. Подставляя в приведённые в таблице уравнения значения концентрации реагента в разные моменты времени, вычисляют значения константы скорости. Частный порядок реакции по данному веществу равен порядку того кинетического уравнения, для которого величина константы скорости остаётся постоянной во времени.
20. Сложные реакции. Обратимые реакции первого порядка. Параллельные реакции. Последовательные реакции. По степени сложности: В зависимости от механизма реакции могут быть подразделены на простые и сложные. К простым реакциям относятся реакции, протекающие в одном направлении и включающие один химический этап. Формально они классифицируются по порядку (когда стехиометрический и кинетический порядки совпадают) и могут быть нулевого, первого, второго, третьего порядков. В «чистом виде» простые реакции почти не встречаются. В подавляющем большинстве случаев это стадии сложных химических процессов. Сложные реакции – это многостадийные химические процессы. В кинетике существует положение о независимом протекании отдельных стадий сложной реакции: значение константы скорости отдельной стадии не зависит от наличия в системе других стадий. Сложные реакции подразделяются следующим образом: - обратимые реакции: А + В Х + У - параллельные реакции: C + D А + В G + R В случае параллельных реакций скорость всего процесса будет определяться скоростью наиболее быстрой его стадии. - последовательные реакции: А ® В ® С или А + В ® С + D ® Х + У Если в последовательных реакциях скорость одной из химических стадий значительно меньше скоростей других, то скорость всего процесса будет определяться скоростью самой медленной стадии. Пример – реакции взаимного превращения изомеров. В общем случае стехиометрическое уравнение реакции первого порядка имеет вид А
Реакция протекает одновременно в двух противоположных направлениях, поэтому скорость такой реакции равна разности скоростей прямой и обратной реакций, каждая из которых является реакцией первого порядка: – a, b – исходное количество веществ А и В (моль); x – количество вещества А (моль), прореагировавшее к моменту времени t.
После преобразования
– ln (L – x) + ln L = (k 1 + k 2) t, k 1 + k 2 = Таким образом, для нахождения k 1 + k 2 надо знать L. L =
(числитель и знаменатель первого выражения делим на k 2; k 1 / k 2 = K – константе равновесия). Для нахождения Lнадо знать K. В момент равновесия скорости прямой и обратной реакций одинаковы:
x ¥ – количество вещества А, прореагировавшее к моменту равновесия. K = Зная K, найдем L и найдем k 1 + k 2 и k 1, k 2 в отдельности. Иногда обратимую реакцию 1-го порядка формально удобно рассматривать как необратимую. Можно считать, что к концу реакции прореагирует x ¥ моль исходного вещества. Тогда дифференциальное уравнение скорости реакции будет иметь вид
k = Из сопоставления уравнений для k 1 + k 2 и k видно: k = k 1 + k 2, L = x ¥. Реакции, в которых исходные вещества способны образовывать разные продукты реакции или одно вещество одновременно способно реагировать с несколькими веществами, называются параллельными.
Скорости превращения по каждому из параллельных путей
где x 1 и x 2 – концентрации А, превращенного в В и С соответственно, x = x 1 + x 2. Отношение скоростей этих процессов
при любом τ постоянно (принцип независимости химических реакций). Последовательными называют реакции с промежуточными стадиями, когда продукт предыдущей стадии служит исходным веществом для последующей:
Зависимость концентраций реагентов этой двустадийной реакции приведена на рис. 5.6.
При k 1 >> k 2 все исходное вещество может превратиться в промежуточный продукт В, прежде чем начнется вторая реакция. Скорость всей реакции определяется второй стадией. При k 1 << k 2 концентрация промежуточного продукта мала, поскольку он не успевает накапливаться; эта стадия определяет скорость реакции в целом. Таким образом, скорость определяется самой медленной стадией (принцип лимитирующей стадии).
21. Сопряженные реакции. Цепные реакции. Фотохимические реакции. Сопряжённые реакции. Сопряжёнными принято называть сложные реакции, протекающие следующим образом: 1) А + В ––> С 2) А + D ––> Е, причём одна из реакций может протекать самостоятельно, а вторая возможна только при наличии первой. Вещество А, общее для обеих реакций, носит название актор, вещество В – индуктор, вещество D, взаимодействующее с А только при наличии первой реакции – акцептор. Например, бензол в водном растворе не окисляется пероксидом водорода, но при добавлении солей Fe(II) происходит превращение его в фенол и дифенил. Механизм реакции следующий. На первой стадии образуются свободные радикалы: Fe2+ + H2O2 ––> Fe3+ + OH– + OH• которые реагируют с ионами Fe2+ и бензолом: Fe2+ + OH• ––> Fe3+ + OH– C6H6 + OH• ––> C6H5• + H2O Происходит также рекомбинация радикалов: C6H5• + OH• ––> C6H5ОН C6H5• + C6H5• ––> C6H5–C6H5 Т.о., обе реакции протекают с участием общего промежуточного свободного радикала OH•. Цепные реакции К цепным реакциям относят реакции, протекающие с образованием свободных радикалов, способных превращать реагенты в конечные продукты, поддерживая постоянство свободных радикалов или даже увеличивая их (разветвленная цепная реакция).
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |



 Диссоциация — распад молекулы, связанный с разрывом одной связи:
Диссоциация — распад молекулы, связанный с разрывом одной связи:


 Реакции электрофильного и нуклеофильного замещения— реакции замены активной группы в молекуле на другую группу:
Реакции электрофильного и нуклеофильного замещения— реакции замены активной группы в молекуле на другую группу:



 Реакция элиминирования — распад многоатомной молекулы на несколько молекул:
Реакция элиминирования — распад многоатомной молекулы на несколько молекул:

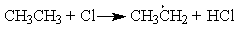
 Реакция рекомбинации — взаимодействие двух атомов, радикалов, ионов, приводящее к образованию молекулярного продукта:
Реакция рекомбинации — взаимодействие двух атомов, радикалов, ионов, приводящее к образованию молекулярного продукта:
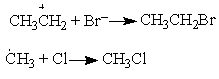 Реакция диспропорционирования—перераспределение атомов или их группировок между двумя одинаковыми молекулами, радикалами в результате их взаимодействия:
Реакция диспропорционирования—перераспределение атомов или их группировок между двумя одинаковыми молекулами, радикалами в результате их взаимодействия:

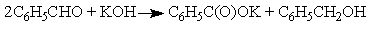

 следует записать следующим образом:
следует записать следующим образом: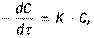 (11)где С – концентрация реагента А.
(11)где С – концентрация реагента А.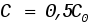 , получаем для времени полупревращения t1/2 реакции первого порядка выражение:
, получаем для времени полупревращения t1/2 реакции первого порядка выражение: (12)
(12)
 , (13)
, (13)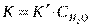 ;
;  -концентрация воды.
-концентрация воды. (14)
(14) (15)
(15)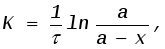 (16)
(16) , (17)
, (17) (18)
(18) (II.5)
(II.5) (II.6)
(II.6) (II.7)
(II.7) (II.8)
(II.8) (II.9)
(II.9)
 (II.10)
(II.10) (II.11)
(II.11) (II.12)
(II.12) (II.13)
(II.13)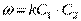
 , то
, то  .
. . Разделим переменные и проинтегрируем:
. Разделим переменные и проинтегрируем:  и получим:
и получим: уравнения реакций второго порядка;
уравнения реакций второго порядка; 
 ).
).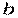
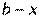

 уравнение реакции второго порядка;
уравнение реакции второго порядка; 
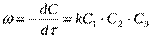
 , уравнение примет вид:
, уравнение примет вид:  .
.



 кроме реакции первого порядка (n=1)
кроме реакции первого порядка (n=1) (34)
(34) , для второго порядка (когда начальные концентрации реагентов одинаковы) - в системе
, для второго порядка (когда начальные концентрации реагентов одинаковы) - в системе  и для третьего порядка - в системе
и для третьего порядка - в системе  . Если экспериментальные точки действительно легли на прямую, то оси координат подобраны удачно и соответствуют порядку реакции. По тангенсу угла наклона прямой можно определить константу скорости реакции.
. Если экспериментальные точки действительно легли на прямую, то оси координат подобраны удачно и соответствуют порядку реакции. По тангенсу угла наклона прямой можно определить константу скорости реакции.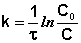


 В.
В.
 = k 1
= k 1  – k 2
– k 2  ,
, = k 1 (a – x) – k 2 (b + x).
= k 1 (a – x) – k 2 (b + x). – x);
– x);  =
=  ,
, ln
ln  .
.
 =
=  .
. =
=  , – ln (x ¥ – x) + ln x ¥ = kt,
, – ln (x ¥ – x) + ln x ¥ = kt,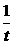 ln
ln  .
.
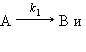
 соответственно равны
соответственно равны