
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Руководство к решению задач по теории вероятностей и математической статистикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Содержание
Тема 1. Основные понятия теории вероятностей…………………………….3 Тема 2. Классические теоремы теории вероятностей………………………12 Тема 3. Повторные независимые испытания………………………………..20 Тема 4. Случайные величины и законы их распределения………………...32 Тема 5. Числовые характеристики случайных величин……………………39 Тема 6. Основные дискретные случайные величины и их числовые характеристики…………………………….………………………. 48 Тема 7. Основные непрерывные случайные величины и их числовые характеристики……………….……………………………………. 55 Тема 8. Закон больших чисел и центральная предельная теорема………..64 Тема 9. Основные понятия математической статистики. Числовые характеристики…………………………….………………………..70 Тема 10. Статистические оценки…………………………………………….85 Тема 11. Корреляция и регрессия……………………………………………94 Тема 12. Проверка статистических гипотез………………………………..109 Литература…………………………………………………………………...117 Приложения………………………………………………………………….
Михаил Филиппович Тиунчик РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ Учебное пособие
Н/К Редактор Г.С.Одинцова ЛР № 020756 от 02.04.98г.
Подписано в печать. Формат 60´84/16. Бумага писчая. Печать офсетная. Усл.п.л. 7,0. Уч.-изд.л. 5,0. Тираж 830 экз. Заказ №. 680042, г.Хабаровск, ул.Тихоокеанская, 134, ХГАЭиП, РИЦ.
ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Испытания и события. Невозможное, достоверное и случайное события. Виды случайных событий. Классическое определение вероятности. Относительная частота и ее устойчивость. Ограниченность классического определения вероятности. Статистическое определение вероятности. Геометрические вероятности. Элементарные события. Пространство элементарных событий. Противоположное событие, сумма и произведение событий. Алгебра событий. Аксиоматическое определение вероятности. Вероятностное пространство. Принципы практической невозможности и практической достоверности событий. Предмет теории вероятностей. Перестановки, сочетания, размещения и формулы для вычисления их числа. Применение комбинаторики к подсчету вероятностей.
Л и т е р а т у р а
[2], гл. 1, § 1,2, гл.2, § 1,2; [3], гл.1, гл. 2, 2.1-2.3, 2.5, гл.3, 3.1; [5], гл.1, § 1-6, гл.2, § 4; [6], гл.1; [7], гл.1; [8], гл.1, § 1-3, § 7; [9], гл.1, § 1-4; [10], гл.1, § 1-3; [11], гл.26, § 182-185; [12], ч.2, гл.1, § 1,2; [13], гл.20, § 1,2; [15], гл.1, § 1-3, гл.2, § 1-3; [16], гл.1, 1.1-1.3, 1.7.
О с н о в н ы е ф о р м у л ы и м е т о д и ч е с к и е У к а з а н и я
Вероятность Р (А) события А вычисляется как отношение числа m благоприятных этому событию исходов к общему числу n равновозможных, единственно возможных и несовместных исходов: Р (А) = Пусть всем возможным результатам испытания соответствуют точки множества W, а данному событию А – точки множества S, которое является частью множества W (S Р (А) = где mes G - длина, площадь, объем множества G. Частота W(А) события А находится на основании результатов опыта по формуле W(А) = где n – общее число фактически проведенных испытаний, а m – число появления события А. Число перестановок Рn из n элементов находится по формуле Рn = n! По определению принимают равенство 0!=1. Число сочетаний
В частности, Число размещений
При решении задач на классическое определение вероятности прежде всего выясняют, в чем состоят исходы испытания и какие исходы благоприятны данному событию. Затем непосредственно вычисляют вероятность события по формуле (1.1), предварительно вычислив общее число исходов n и число m благоприятных исходов. При этом надо убедиться, что указаны все элементарные исходы и что они равновозможны и несовместны. При выявлении элементарных исходов иногда допускаются ошибки. Поясним это на примере. Монета бросается 2 раза. Найти вероятность того, что герб выпадет оба раза (событие А). Решая эту задачу, рассуждают так. Герб может выпасть 2 раза, 1 раз и 0 раз (ни разу). Считают, что элементарных исходов три: {0,1,2}. Эти исходы несовместны и единственно возможны. Благоприятен А один исход (герб выпал оба раза). Тогда Р (А) = Приведенное решение содержит ошибку. На самом деле описанные выше исходы не являются равновозможными, и поэтому нельзя применять классическое определение вероятности. Пространством Решение многих задач основывается на двух фундаментальных правилах, называемых правилами суммы и произведения. Правило суммы можно сформулировать так: если некоторый объект Правило суммы обобщается на любое конечное число объектов. Правило произведения состоит в следующем: если объект Это правило обобщается на случай k объектов. Тогда число комбинаций ( В частности, может быть k одинаковых групп по n элементов в каждой. Пусть на r-м шаге выбирается элемент из r-й группы. Тогда число N различных комбинаций есть nk. Приведем пример. Цифровой замок содержит на общей оси 4 диска, каждый из которых разделен на 6 секторов, отмеченных цифрами. При наборе кода каждый диск может быть установлен в любую из 6 позиций. Следовательно, замок содержит N=64 различных четырехзначных кодов. При решении задач встречаются выборки без возвращения и выборки с возвращением. Выборку без возвращения наглядно можно представить как последовательный набор из совокупности n перенумерованных шаров, находящихся в урне. Вынутые шары в урну не возвращаются. При выборке с возвращением шары вынимаются, запоминаются и возвращаются в урну. В последнем случае один и тот же шар может быть выбран более одного раза. Если производится выбор с возвращением, то число различных выборок объема k из множества в n элементов равно nk. К выборкам без возвращения относятся размещения, перестановки и сочетания, которые часто применяются при непосредственном вычислении вероятностей по формуле (1.1). Для вычисления числа перестановок, сочетаний и размещений применяются, соответственно, формулы (1.4)-(1.6). Перестановки из n элементов можно понимать как размещения из n элементов по n элементов. Важно уяснить различие между сочетаниями и размещениями. Поясним это на примере. В группе 25 студентов. Сколькими способами можно выбрать: 1) трех делегатов на конференцию; 2) актив группы (старосту, заместителя старосты, профорга)? В первой ситуации нас интересует только состав, поэтому речь идет о сочетаниях. Применяя формулу (1.5), получим N= При подсчете числа сочетаний для уменьшения вычислительной работы надо руководствоваться следующим. Если m
которая следует из (1.5). Если m> Например,
З а д а ч и 1. В районе 8 населенных пунктов. Сколько различных маршрутов для самолета можно составить, если известно, что каждый маршрут соединяет три пункта? 2. Сколько различных «слов», состоящих не менее чем из четырех разных букв, можно образовать из букв слова «ученик»? 3. На четырех карточках написаны числа 1, 3, 4, 5. Найти вероятность того, что сумма чисел на трех произвольно выбранных карточках делится на 4. 4. Данное предприятие в среднем выпускает 20% продукции высшего сорта и 70% продукции первого сорта. Найти вероятность того, что случайно взятое изделие окажется первого или высшего сорта. 5. В цехе работают 7 мужчин и 5 женщин. По табельным номерам наудачу отобраны 3 человека. Определить вероятность того, что все отобранные 1) мужчины, 2) женщины. 6. В группе трое юношей и 21 девушка. По жребию разыгрываются два билета в театр. Какова вероятность того, что в театр пойдут: 1) две девушки, 2) одна девушка и один юноша, 3) лица одного пола? 7. Из 6 менеджеров, 4 бухгалтеров и 5 инженеров необходимо случайным образом сформировать комиссию в составе 6 человек для анализа работы фирмы. Найти вероятность того, что в комиссию войдут 3 менеджера, 2 бухгалтера и один инженер. 8. На склад торгового центра завезено 120 мешков сахарного песка. Среди этих мешков 10 имели избыточную влажность. Для продажи случайно отобрали 15 мешков. Определить вероятность того, что на продажу поступило 2 мешка сахара с избыточной влажностью. 9. Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не имеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга». 10. Определить вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы а, а, а, н, н, с, получится слово «ананас». 11. Наудачу взятый телефонный номер состоит из 6 цифр. Какова вероятность того, что в нем все цифры различны? 12. В прямоугольнике с основанием 8 см и высотой 6 см вписан эллипс. Указать вероятность того, что точка, брошенная наудачу в прямоугольник, окажется внутри эллипса.
ТЕМА 2. КЛАССИЧЕСКИЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Произведение событий. Независимые, попарно независимые и независимые в совокупности события. Теоремы умножения вероятностей независимых событий. Зависимые события. Условная вероятность. Теоремы умножения вероятностей зависимых событий. Сумма событий. Несовместные и попарно несовместные события. Теоремы сложения вероятностей несовместных событий. Полная группа событий. Теорема о сумме вероятностей событий, образующих полную группу. Противоположные события и теорема о сумме их вероятностей. Вероятность появления хотя бы одного из независимых в совокупности событий. Совместные события. Теоремы сложения вероятностей совместных событий. Гипотезы, формулы полной вероятности и Байеса.
Л и т е р а т у р а
[2], гл. 1, § 4, гл.2, §2-4; [3], гл.3, [5], гл. 2, §1-3, гл.3, §1-5, гл.4, § 1-3; [6], гл.1; [7], гл. 2-4; [8], гл.1, § 4-6, [9], гл.1, § 5-8; [10], гл.1, § 4,5; [11], гл.27, § 186-188; [12], ч.2, гл.1, § 3,4; [13], гл.20, § 3-6; [15], гл.3; [16], гл.1, 1.3 - 1.5.
О с н о в н ы е ф о р м у л ы и м е т о д и ч е с к и е У к а з а н и я
Вероятность Р (АВ) произведения АВ двух независимых событий А и В равна произведению вероятностей этих событий: Р (АВ) = Р (А) Р (В). (2.1) Вероятность произведения нескольких независимых в совокупности событий вычисляется по формуле Р (А1 ××× Аn) = Р (А1) ××× Р (Аn). (2.2) Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную в предположении, что первое уже наступило: Р (АВ) = Р (А) Р А(В) = Р (В) Р В(А). (2.3) Для вычисления вероятности произведения нескольких зависимых событий имеет место формула Р (А1 ××× Аn) = Р (А1) Р Вероятность Р (А+В) суммы А+В двух несовместных событий А и В равна сумме вероятностей этих событий: Р (А+В) = Р (А) + Р (В). (2.5) Вероятность появления одного из нескольких попарно несовместных событий вычисляется по формуле Р (А1+ ××× + Аn) = Р (А1) + ××× + Р (Аn). (2.6) Сумма вероятностей событий А1, …, Аn, образующих полную группу, равна единице, т.е. Р (А1) + ××× + Р (Аn) = 1. (2.7) В частности, сумма вероятностей двух противоположных событий А и Р (А) + Р ( Вероятность Р появления хотя бы одного из нескольких независимых в совокупности событий А1,…, Аn находится по формуле Р = 1 – Р ( Если события А1,…, Аn имеют одинаковую вероятность, равную р, то вероятность Р появления хотя бы одного из них вычисляется по формуле Р = 1 – qn, (2.10) вытекающей из формулы (2.9) (q – вероятность противоположных событий Вероятность суммы двух совместных событий находится по формуле Р (А+В) = Р (А) + Р (В) – Р (АВ). (2.11) З а д а ч и
1. Покупатель приобрел электрокофеварку и электрокофемолку. Вероятность выхода из строя в течение гарантийного срока для электрокофеварки равна 0,05; а для электрокофемолки такая вероятность равна 0,1. Определить вероятность того, что оба прибора выдержат гарантийный срок. 2. Для некоторой местности число ясных дней в августе равно 20. Определить вероятность того, что первого и второго августа будет хорошая погода. 3. На каждой из семи одинаковых карточек написана одна из букв А, В, О, Р, С, Т, А. Какова вероятность того, что, 1) извлекая наугад все карточки по одной, получим в порядке их выхода слово «Саратов»; 2)извлекая 5 карточек, получим в порядке их выхода слово «товар»? 4. В урне находятся 40 черных, 26 коричневых, 22 красных и 12 синих шаров. Найти вероятность того, что вынутый наудачу из урны шар окажется синим или красным. 5. Хлебозавод выпускает в среднем 27% продукции высшего сорта и 62% продукции первого сорта. Найти вероятность того, что случайно взятое изделие окажется первого или высшего сорта. 6. Контрольная работа по теории вероятностей состоит из трех упражнений. Вероятность того, что студент решит упражнение на закон распределения для дискретной случайной величины, равна 0,6, на закон распределения для непрерывной случайной величины – 0,7, на нормальный закон – 0,9. Какова вероятность того, что студент напишет контрольную работу, если для этого достаточно решить не менее двух упражнений. 7. В двух урнах находятся шары, причем в первой урне 5 белых, 9 черных и 6 красных шаров, а во второй – 5 белых, 8 черных и 7 красных. Из каждой урны наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета? 8. Вероятность поражения цели одной ракетой 0,95, а другой – 0,9. Найти вероятность того, что цель будет поражена, если выпущены по ней обе ракеты. 9. Вероятность того, что саженцы сливы, яблони, абрикоса приживутся при осенней посадке соответственно равны 0,9; 0,7 и 0,6. На участке высадили по одному саженцу каждого вида. Какова вероятность того, что 1) приживутся все саженцы; 2) приживется только один саженец; 3) приживется хотя бы один саженец? 10. Вероятность поражения цели при трех выстрелах из одного орудия равна 0,992. Какова вероятность поражения цели в одном отдельном выстреле? 11. Приборы изготавливаются на трех заводах. Первый завод производит 45% общего количества приборов, второй – 35%, третий – 20%. Первый завод выпускает 70% приборов высшего качества, второй – 80%, третий – 90%. В институт поступает продукция всех заводов. Какова вероятность того, что взятый для работы прибор окажется высшего качества? 12. Вероятности обращения фирмы за кредитом в один из трех банков соответственно равны: р1=0,5; р2=0,3; р3=0,2. Вероятность предоставления кредита в первом банке равна 0,6, во втором – 0,4, в третьем – 0,3. Найти вероятность того, что фирма получит кредит при обращении в наудачу выбранный банк. 13. На склад поступает продукция трех фабрик. При этом продукция первой фабрики составляет 20% общего поступления, второй – 35%, третьей – 45%. Известно, что первая фабрика выпускает 3% нестандартных изделий, вторая - 2%, третья – 1%. Наудачу взятое на складе изделие оказалось нестандартным. Определить вероятность того, что это изделие выпущено третьей фабрикой. 14. Три бухгалтера обрабатывают счета. При этом первый делает 2/5 всей работы, а два других выполняют оставшуюся часть работы в равной доле. Вероятность того, что первый бухгалтер допустит ошибку при работе над отдельным счетом, равна 0,01; для второго бухгалтера эта вероятность равна 0,004, а для третьего – 0,005. При проверке счетов была найдена ошибка. Каким вероятнее бухгалтером она допущена?
Л и т е р а т у р а
[2], гл.1, § 3, гл.5, § 3-5; [3], гл.4; [5], гл.5, § 1-4, гл.6, § 5,6; [6], гл.1; [7], гл.5, 6; [8], гл.2, § 1-3; [9], гл.2, § 1-5; [11], гл.28, § 189-195; [12], ч.2, гл.2, § 5-8; [13], гл.20, § 8; [15], гл.4, § 1-3.
О с н о в н ы е ф о р м у л ы и м е т о д и ч е с к и е у к а з а н и я Если производится n повторных независимых опытов, в каждом из которых появляется либо событие А с вероятностью р, либо событие Р n(m) = Вероятность того, что А появится хотя бы один раз при n повторных независимых испытаниях, вычисляется по следующей формуле: Рn (m ³ 1) = 1 – qn. (3.2) Наивероятнейшая частота m0 удовлетворяет неравенствам np – q £ m0 £ np + p. (3.3) Если число np+p – целое, то наивероятнейшее число m0 имеет только одно значение. Этим значением будет целая часть числа np+р. Если np+p – число дробное, то m0 принимает два значения: m0=np-q=np+p-1 и m0=np+p. При достаточно большом числе проведенных испытаний m0 примерно равно np (m0 » np). При большом числе испытаний для вычисления Рn(m) применяются следующие приближенные равенства: Рn(m)»
Рn(m)» В литературе обычно имеются таблицы значений функции Вероятность того, что событие А наступит не менее k раз и не более r раз, находится по приближенной формуле Р n (k £ m £ r)» Ф где Ф(х) = Формула (3.4) называется локальной теоремой Муавра-Лапласа, формула (3.6) – интегральной теоремой Муавра-Лапласа. Формулу (3.5) называют теоремой Пуассона. Вероятности отклонений частоты m от наивероятнейшей частоты m0 и относительной частоты W от постоянной вероятности р события А при достаточно больших n вычисляются, соответственно, по следующим приближенным формулам: Р n Р n где Ф(х) – функция Лапласа и При n®¥ величина 2Ф При практическом применении теории вероятностей часто встречаются задачи на повторение опытов (испытаний). Многие же задачи моделируются как задачи на повторные испытания. Решаются они просто в случае, когда опыты являются независимыми. В этом прежде всего и надо убедиться. В каждом отдельном опыте появляется либо событие А, либо ему противоположное Может быть и более общая схема: независимые опыты производятся в различных условиях (вероятность события А от опыта к опыту меняется). Имеется способ вычисления Р n(m) и в этой ситуации (см., например, [3]). Примерами независмых опытов являются: неоднократное бросание монеты (игральной кости), многократное извлечение карты из колоды (шара из урны, изделия из партии) при условии, что выбранный предмет возвращается. Иногда допускают ошибку. В отборах без возвращения применяют биномиальное распределение (формулу Бернулли), на самом же деле надо применять гипергеометрическое распределение. Поясним это разбором задачи. В урне находятся 5 белых и 10 черных шаров. Из урны наугад извлекли 3 шара. Какова вероятность того, что два из них окажутся белыми? Решение (ошибочное). Обозначим через А событие, состоящее в том, что отдельно взятый шар будет белым. Тогда, согласно условию, за р принимают число Р 3(2) =
Приведенное решение было бы верным, если бы опыты проводились в неизменных условиях. Для этого шары надо обратно возвращать в урну и перемешивать. По условию нашей задачи из урны вынули три шара (следовательно, они не возвращались). В этом случае уже нельзя говорить о неизменности условий всех трех опытов, так как после каждого извлечения состав шаров в урне будет меняться. Для правильного решения применим классический способ подсчета вероятностей. Число возможных исходов будет Формула Бернулли (3.1) дает точное значение Р n(m), однако для больших значений n и m появляются вычислительные трудности, прежде всего из-за выражения для Поэтому возникает необходимость в более простых формулах для Р n(m). Таковыми являются формулы (но уже приближенные) (3.4) и (3.5). Формула (3.4) дает тем более близкие к точному значению Р n(m) результаты, чем больше значение Найдем наибольшее значение выражения pqºр(1-р). Рассмотрим функцию f(р)=р(1-р)ºр-р2, 0 £ р £ 1. Очевидно, что она достигает своего наибольшего значения В случае, если вероятность р близка к нулю и число n мало, формула (3.4) дает заметные отклонения от формулы Бернулли. Асимптотическая формула (3.5) применяется для редких событий (со значениями р, близкими к нулю). Приближение тем лучше, чем больше n и меньше p. Обычно формулой (3.5) пользуются при условии Задачи с редкими событиями встречаются на практике в лотереях, страховании, при проверке качества изделий с низким процентом брака, в медицине (рождение близнецов, заболевание редкой инфекционной болезнью) и т.п. Если р близко к единице (например, р³0,97), то q близко к нулю (q£0,03). Тогда формулу Пуассона (3.5) можно применить для вычисления вероятности того, что Как уже отмечалось, для функций Поясним метод линейного интерполирования для нашей ситуации. Аргумент y-y1= В ряде учебников имеются таблицы значений функции р(m, Если число n независимых испытаний мало и надо вычислить вероятность появления события А от k до r раз, то надо применить следующую формулу: Р n(k £ m £ r) = Эту последнюю формулу можно применять и при достаточно большом числе испытаний, если в сумме справа число слагаемых невелико (мало число r-k). При этом для вычисления Р n(m) при малых значениях р (р£0,03) надо применять приближенную формулу (3.5), а в остальных случаях – (3.4). Если же число n велико и число слагаемых в сумме В этой формуле участвует функция Лапласа Ф(х), называемая еще интегралом вероятностей. Значения этой функции приводятся почти в каждом из рекомендуемых учебников. Только надо помнить, что в ряде учебников (см., например, [7], [8], [11]) эти значения удвоены. Тогда в (3.6) надо подставлять значения в два раза меньшие (можно также, не уменьшая этих значений, ввести справа в (3.6) множитель Таблицы Ф(х) приведены для х ³0. Для отрицательных аргументов значения этой функции находятся на основании ее свойства, что Ф(- х) = -Ф(х). Например, Ф(-2) = -Ф(2)» -0,4 772 (см. [5], приложение 2). Далее, для х >5 приближенно полагают Ф(х)» Сделаем некоторые пояснения по поводу формулы (3.8). Прежде всего она имеет теоретическое значение. Из нее следует так называемый закон больших чисел Бернулли, который будет рассмотрен в дальнейшем. Она объясняет, что статистическое определение вероятности события введено разумно. Эта формула имеет значительные практические приложения. Зная р, n и e, из (3.8) находим надежность g. Если известны р, n и g, то можно найти точность e. Наконец, что очень важно на практике, можно по р, заданным e и g оценить число n (число испытаний, необходимых для какого-нибудь контроля). Более того, можно оценить n только при известных e и g (р- неизвестно). Надежность g приближенно получается из равенства (3.8): g = 2Ф Обозначим через
Решая уравнение (3.9) (g = 2Ф( e = Тогда с надежностью g определяются границы, в которых заключены частость и частота события в серии из n испытаний:
Из (3.10) получается и формула для определения необходимого числа n испытаний при известных р, g, e:
Из последнего равенства при неизвестном р в силу оценки pq=p(1-p)£
З а д а ч и
1. В хлопке содержится 20% коротких волокон. Определить вероятность того, что среди пяти отобранных наудачу волокон окажется три длинных. 2. Письменная экзаменационная работа по математике состоит из пяти задач, причем за решение любой задачи ставится 1 балл. Вероятность решения любой задачи для некоторого абитуриента равна 0,8. Определить вероятность того, что этот абитуриент получит за экзамен не менее 4 баллов. 3. По данным технического контроля в среднем 15% изготовляемых на заводе часов нуждаются в дополнительной регулировке. Найти вероятность того, что из 300 изготовленных за смену часов 240 не будут нуждаться в дополнительной регулировке. 4. В стаде, содержащем 2 000 овец, проводятся прививки против заболеваний животных. Какова вероятность того, что при вакцинации заболеют три овцы, если вероятность заболевания каждого животного при вакцинации равна 0,001? 5. Счетчик Гейгера регистрирует частицы, вылетающие из некоторого радиоактивного источника, с вероятностью 0,0 002. Какова вероятность того, что счетчик зарегистрировал 4 частицы, если за время наблюдения из источника вылетело 15 000 частиц? 6. Вероятность того, ч
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.205.149 (0.012 с.) |


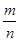 . (1.1)
. (1.1) W). Тогда
W). Тогда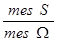 , (1.2)
, (1.2)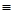
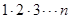 . (1.4)
. (1.4) из n элементов по m элементов вычисляется по формуле
из n элементов по m элементов вычисляется по формуле (1.5)
(1.5) . Это согласуется с тем, что в множестве из n элементов имеется только одно подмножество из 0 элементов – пустое множество.
. Это согласуется с тем, что в множестве из n элементов имеется только одно подмножество из 0 элементов – пустое множество.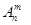 из n элементов по m находится по формуле
из n элементов по m находится по формуле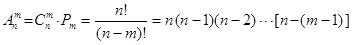 . (1.6)
. (1.6)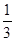 .
. элементарных событий является следующее множество равновозможных событий: {ГГ, ГЦ, ЦГ, ЦЦ}. Через Г обозначено появление герба, а через Ц – цифр (решки). Ошибка первоначального рассуждения в том, что учтен только один из симметричных исходов ГЦ, ЦГ. Таким образом, Р (А) =
элементарных событий является следующее множество равновозможных событий: {ГГ, ГЦ, ЦГ, ЦЦ}. Через Г обозначено появление герба, а через Ц – цифр (решки). Ошибка первоначального рассуждения в том, что учтен только один из симметричных исходов ГЦ, ЦГ. Таким образом, Р (А) = 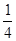 .
.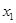 можно выбрать n1 способами, а объект
можно выбрать n1 способами, а объект 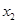 - n2 способами, причем любой способ выбора
- n2 способами, причем любой способ выбора 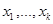 ) есть N=n1…nk.
) есть N=n1…nk.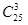 =2300. Во второй ситуации в каждой выбранной тройке студентов можно перераспределять должности, т.е. речь идет о составе и порядке (о размещениях). Тогда по формуле (1.6) N=
=2300. Во второй ситуации в каждой выбранной тройке студентов можно перераспределять должности, т.е. речь идет о составе и порядке (о размещениях). Тогда по формуле (1.6) N=  , то применяют формулу
, то применяют формулу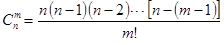 ,
,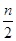 , то надо воспользоваться свойством
, то надо воспользоваться свойством 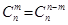 и к вычислению
и к вычислению  применять последнюю формулу.
применять последнюю формулу.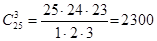 . Вычислим теперь
. Вычислим теперь 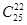 . Воспользовавшись указанным свойством, получим
. Воспользовавшись указанным свойством, получим  .
.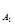 (А2) Р
(А2) Р 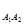 (А3) ××× Р
(А3) ××× Р 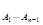 (Аn). (2.4)
(Аn). (2.4) равна единице:
равна единице: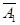 ) ××× Р (
) ××× Р (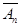 ). (2.9)
). (2.9) ).
). (3.4)
(3.4)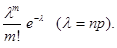 (3.5)
(3.5)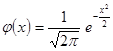 и выражения р(m, λ) =
и выражения р(m, λ) =  .
. - Ф
- Ф  , (3.6)
, (3.6)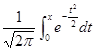 - функция Лапласа, для которой имеется таблица значений.
- функция Лапласа, для которой имеется таблица значений. Ф
Ф  , (3.7)
, (3.7)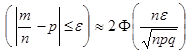 , (3.8)
, (3.8)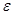 - любое положительное число.
- любое положительное число. Ф
Ф 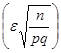 стремится к единице. Тогда событие
стремится к единице. Тогда событие  практически достоверно. Если число
практически достоверно. Если число 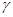 , определяемая равенством
, определяемая равенством 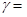 Р n
Р n 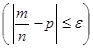 , называется надежностью. Таким образом, надежность есть вероятность совпадения частоты W=
, называется надежностью. Таким образом, надежность есть вероятность совпадения частоты W=  .
. : р=
: р=  . Далее, полагают n=3, m=2. Вероятность искомого события (два белых шара при вынутых трех) вычисляют по формуле Бернулли:
. Далее, полагают n=3, m=2. Вероятность искомого события (два белых шара при вынутых трех) вычисляют по формуле Бернулли: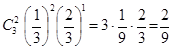 .
.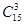 , из них благоприятными для интересующего нас события будут
, из них благоприятными для интересующего нас события будут  исходов. Тогда искомая вероятность Р =
исходов. Тогда искомая вероятность Р = 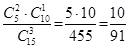 .
.
 . При этом здесь сказывается не только значение n, но и значение pq. Обычно формулой (3.4) пользуются, когда npq³20. Из этого ограничения видно, что чем ближе одно из чисел p или q к нулю (другое число будет близко к единице), тем большим надо брать n. Погрешность этой формулы порядка
. При этом здесь сказывается не только значение n, но и значение pq. Обычно формулой (3.4) пользуются, когда npq³20. Из этого ограничения видно, что чем ближе одно из чисел p или q к нулю (другое число будет близко к единице), тем большим надо брать n. Погрешность этой формулы порядка 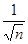 .
.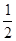 . Следовательно, при одних и тех же значениях n формула (3.4) дает тем лучшее приближение к значению Р n(m) из формулы Бернулли, чем ближе pq к своему наибольшему значению 0,25, т.е. чем ближе р (отсюда и q) к 0,5.
. Следовательно, при одних и тех же значениях n формула (3.4) дает тем лучшее приближение к значению Р n(m) из формулы Бернулли, чем ближе pq к своему наибольшему значению 0,25, т.е. чем ближе р (отсюда и q) к 0,5. =np£10. Погрешность формулы (3.5)
=np£10. Погрешность формулы (3.5) 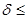 np2.
np2.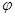 (х) и р(m,
(х) и р(m, 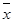 , которого нет в таблице, будет заключен между некоторыми двумя аргументами х 1 и х 2, имеющимися в таблице (х 1 <
, которого нет в таблице, будет заключен между некоторыми двумя аргументами х 1 и х 2, имеющимися в таблице (х 1 < 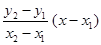 ; ограничение х 1 ¹ х 2 выполняется автоматически, т.к. х 1< х 2. Получилась линейная функция y=
; ограничение х 1 ¹ х 2 выполняется автоматически, т.к. х 1< х 2. Получилась линейная функция y= 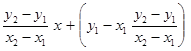 . Значение этой линейной функции в точке
. Значение этой линейной функции в точке  для некоторых m и
для некоторых m и 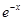 (одного множителя нашей функции). Значения второго множителя
(одного множителя нашей функции). Значения второго множителя 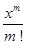 при небольших значениях m легко вычислить.
при небольших значениях m легко вычислить. Р n(m). В этой ситуации k и r не могут быть большими (мало n) и все Р n(m) можно вычислить по формуле Бернулли. Приведенная формула есть следствие теоремы о вероятности суммы попарно несовместных событий.
Р n(m). В этой ситуации k и r не могут быть большими (мало n) и все Р n(m) можно вычислить по формуле Бернулли. Приведенная формула есть следствие теоремы о вероятности суммы попарно несовместных событий.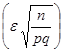 . (3.9)
. (3.9)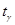 величину e
величину e 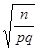 :
: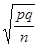 .
.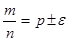 ,
, 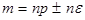 .
.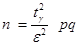 .
.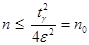 , т.е. достаточно провести n0 испытаний для определения неизвестной вероятности р появления события с заданной точностью и надежностью.
, т.е. достаточно провести n0 испытаний для определения неизвестной вероятности р появления события с заданной точностью и надежностью.


