
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача математического программирования (мп) и ее свойства. Классификация задач мп.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Билет №1 Практика и теория поиска лучших решений. Структуризация эко-ких задач. Си-ма – совоку-ть взамосвязанных эл-тов, обладающая определенной целостностью (относительной изолированностью от вн. среды) и присущей целью развития. Бывают: простые и сложные, большие и малые. Сложность си-мы зависит от доступности инф-ции по упра-нию этой си-мой. Си-ма простая, если есть инф-ция доступная и достаточная для упра-ния. Иначе – сложная. Модель- исп-тся для целец познания объектов и процессов. Пример:объект- земной шар, мо-ли – глобус,карта. Мо-ль- заме-тель оригинала, отража-ий его хара-ки, существенные с позиции упра-ния, т.о. что изучение мо-ли дает новые сведения об оригинале. Отл от др инструментов тем, что они ориенти-ны на косвенное изучение. Класифи-ция моделей: физ-кие и абстрактыне, реальные и символьные, образные и словестные. ЭМ мо-ль – отражение упра-мого объекта с помощью мат соотно-ний(инструментов). ЭМ мо-ли: лин-ые и нели-ные, непрерывные и дискретные, простран-ные и точечные. Реальные мо-ли хар-тся стохастичностью (неопре-ый хар-тер). Математическое программирование ("планирование")– это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Эк-мат классиф моделей: 1. По типу мат описания – линейное и Нелинейное; 2. геометрические, выпуклые, Целочисленные (дискретные –переменные только целые), Стохастические, Динамические (время учит-ся явным образом); 3. Точечные (EX. Прибыль за год), Пространствен (Ex.логистика - отраж простран аспекты). Линейное программирование (ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие: 1) показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X=(x1,x2,…,xn); 2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Билет № 2 Компромиссный критерий Гурвица и его истолкование. Проблема выбора параметров критерия.
Это компромисс между крайним пессимизмом и умеренным оптимизмом. 0≤α≤1, α – степень пессимизма оперирующей стороны. 1 – пессимист, 0 – оптимист. H = αmax i(minj aij) (пессимист)+ (1-α)max i(minj aij). H =max[α minj aij + (1-α)maxj aij]. –критерий Гурвица.
Билет №3 Задача математического программирования (МП) и ее свойства. Классификация задач МП. Математическое программирование ("планирование")– это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так распределительных задач. Анализируемые процессы считаются многократно повторяющимися и следовательно ими можно управлять. 1. Мат. программирование – один из разделов математики, который изучает методы нахождения условного экстремума ф-ии многих переменных. Разделы мат. программирования: 1) линейное программирование: f(x) стремится min(max), x принадлежит X. целевая ф-ия явл. линейной, а множ-во Х задается системой лин-х равенств и неравенств; 2) нелинейное программирование: а) выпуклое программирование. Относятся задачи на отыскание min-ма ф-ии если мн-во Х выпукло и целевая ф-ия выпукла тоже. min на выпуклом U, max на вогнутом ∩. б) задачи квадратичного программирования, где целевая ф-ия квадратична, а ограничения – линейны. в) многоэкстремальная задача. 3) целочисленное программирование – задачи ЛП при условии что все переменные или некоторые из них явл. целочисленными. Особенности задач МП: 1) классические методы отыскания усл. экстремума ф-ии не работают из-за ограничений типа неравенства; 2) из-за большой размерности задач и большого числа ограничений, проверить все потенциальные экстремальные точки не. Цели МП: создание аналитических методов опр-ия решения, а в случае если это невозможно, то создание эф-х вычислит-х способов получения приближенного решения. Этапы построения мат. моделей: 1) построение качественной модели рассматриваемой задачи (опр-ть все факторы, которые оказывают влияние, установить закономерности которые наиболее значимы); 2) запись с помощью мат. знаков построенной кач. модели (выделение управляющих и управляемых факторов); 3) исследование влияния переменных на значение целевой ф-ии; 4) непосредственное решение поставленной задачи и проверка адекватности модели.
Билет № 4 Выбор решений в условиях недостаточной достоверности статистических характеристик. Понятия единичного эксперимента, идеального и неидеального эксперимента. При исследовании некоторых проблем в условиях неопределённости существует возможность экспериментов, дающих дополнительную информацию об условиях действительных состояний природы и, тем самым, снизить степень неопределённости задачи. Если возможности экспериментов достаточно обширны, то после определённого их количества реальные характеристики состояний природы могут быть оценены с любой необходимой точностью. Основные понятия. Единичным (фиксированным) называется эксперимент, объем и порядок проведения которого заранее определены и не изменяются в процессе его осуществления. Идеальный ЕЭ -такой ЕЭ,который приводит к полной ликвидации неопределённости,т.е. к точной характеристике действительных условий природы. Неидеальный (реальный)ЕЭ -такой ЕЭ,который не приводит к точным сведениям о реальных условиях операции,а даёт только дополнительные свидетельства в пользу тех или других состояний природы.В статистических играх с ЕЭ целесообразность эксперимента и методы выбора наилучшей стратегии оперирующей стороной устанавливаются заранее, до проведения эксперимента - то есть, на основе априорной информации. Д ругое наименование ЕЭ - эксперимент с заданным объемом выборки, т.е. состоящий из последовательности испытаний, объём и порядок проведения которых определены заранее. В ЗПР с ЕЭ предполагается, что эксперимент всегда осуществляется в полном объёме. Однако в некоторых постановках задач предусматривается, что после каждого последовательного испытания возможно прекращение эксперимента и выбор лучшей стратегии на основе уже полученной информации-статистические игры с последовательным экспериментом. Принципиальное отличие ЗПР с последовательным экспериментом от ЗПР с ЕЭ состоит в том, что решение принимается не заранее,а в ходе эксперимента на основе получаемой при этом апостериорной информации. Это даёт дополнительные преимущества в обосновании выбора и, как следствие, вероятность дополнительного эффекта от управления. Другое отличие - возможность менее жёстких требований к точности и достоверности исходной информации, которая последовательно уточняется в результате последовательных испытаний (последовательной выборки). С реди ЗПР с последовательной выборкой выделяют задачи:1)· ЗПР с усечённой последовательной выборкой 2) ЗПР с неограниченной последовательной выборкой. В первом случае устанавливается предельное допустимое число последовательных испытаний (опытов, проб и т.п.). Большинство применяемых в теории статистических решений с экспериментом принципов оптимальности выбора совпадает с уже рассмотренными. Наибольшее применение находит байесовский подход - поиск стратегии, наилучшей в среднем. Применение этого принципа гарантирует получение максимального в среднем результата при многократном проведении операции. Билет №5 Билет 6 Постановка задачи выбора решений в условиях неопределенности с возможность проведения единичного идеального эксперимента. Содержательный анализ возможностей практического использования метода, его достоинств и недостатков.
1).правила проведения, которые определяются до его начала и в процессе реализации не изменяются;2).даём достаточно достоверные вероятности.ИЭ-дающий высоконадежные результаты.ОБЩАЯ ПОСТАНОВКА ЗПР С ЕИЭ.ЦЕЛЬ:1).оценить эффективность применения ЕИЭ до его проведения;2).оценить возможные мах доходы в случае проведения ЕИЭ и в случае отказа.1ШАГ:что можно получить без ЕИЭ(доход?);2ШАГ.Доход с ЕИЭ;3ШАГ:Эффективность ЕИЭ;4ШАГ:целесообразность ЕИЭ.ИНФО К РАСЧЕТАМ:1).Возможные ситуации на рынке Пn(привлечение экспертов);2).возможные стратегии Хm(внутренняя информация);3).Платежная матрица А с достаточно достоверными показателями;4).вектор q – грубые, предварительные;5).затраты на эксперимент(априорные-до;апосториорные-после).1ШАГ:подход Байеса:
Билет №7 Билет 8 Билет 10 Формулировка задачи выбора решений в виде задачи математического программирования (МП) с прямым заданием стохастичности условий. Рассматривается задача ЛП, в которой требуется найти максимум линейной формы Входная информация (детерминированная – однозначно задана) не точная, приближенная, характеризуется неопределенностью Экспертная оценка все-равно используется: 1) средне наибольшая вероятность – оценка математического ожидания (все случайные величины – ξ); 2) коэффициент вариации Кв (NPV)
искомое решение
-3ξ ξ ξ1 ξ2 +3ξ График показывает поведение функции цели как случайной величины не зависимо от количества ресурсов. Вероятностный характер имеет и функция цели (цены) и коэффициенты расхода ресурса (их возможного недостатка). Ресурсы детерминированы, случайной компоненты нет, функция цели – стох.
Используется норм. распределение: НОРМРАСПР (заданная точка; ξ; σ; [0,1])
Р – надежность рез-та (попадание ф-ии цели в правый хвост от задан. гр-цы. Решение: 1) все значения заменяются на мат. ожидании (среднее значение) – максимизация результата при заданной надежности P ≥ Р при Fà max; 2) максимизация надежности при заданном уровне эффекта F ≥ F при maxP(F) Обычно проводят серию расчетов при различных коэффициентах вариации и при различных требованиях к надежности выполнения рес-ных обязательств. Следует ожидать, что с ростом неопределенности и требований к надежности результаты снизятся, т.к. значительная часть ресурсов будет отвлекаться в резервы. Недостаток – не можем сказать, с какой вер-тью получилась функция цели. F(x)àmax – случайная величина, распределенная по нормальному закону (можно подсчитать все ее параметры). В постановках стох. задач рассматривают следующие пок-ли кач-ва решений: - математическое ожидание линейной формы (функции цели); - дисперсия функции цели; - лин. комбинация (компромисс) мат. ожидания и дисперсии ф-ии цели; - вероятность превышения функцией цели некоторого фиксированного порога; - математическое ожидание полезности функции цели; - максимин функции цели (или математического ожидания функции цели).
Билет 11 Содержание двух этапов симплекс-процесса и основные характеристик соответствующих процедур. На предприятии производят два вида продукции - А и Б. Для выпуска единицы продукции А требуется 0.2 ед. труда; Б - 0.4 ед. труда и 0.1 ед. продукции а. Формализация задачи в виде модели ЛП: Найти максимум Х0 при условиях X1 - 0.1X2 = 0.75X0 X2 = 0.25X0 0.2X1 + 0.4X2 + X3 = 100 X=(X1,X2,X3)>=0 Здесь Х0 - валовый выпуск продукции в стоимостном выражении; Х1 и Х2 выпуск продукции А и Б соответственно; Х3 - дополнительная переменна имеющая смысл неизрасходованного труда (резерв рабочего времени). Расширенная задача с включением искусственных переменных для создания единич исходного базиса: Найти максимум Х0-МW1-MW2 при условиях X1 - 0.1X2 - 0.75X0 + W1 = 0 X2 - 0.25X0 + W2 = 0 0.2X1 + 0.4X2 + X3 = 100 X = (X1,X2,X3) >= 0 Смысл условий: первое условие есть баланс выпуска и расхода продукции А; второе условие учитывает при выпуске продукции Б расход промежуточного продукта А; третье условие есть баланс рабочего времени (труда). Коэффициенты разложения по базису W1, W2, X3 векторов-столбцов матрицы услов совпадают с самой матрицей, ибо базис - единичная матрица. 1 этап: в соответствии с алгоритмом осущ-ся исключение искусств переменных W1 и W2 из базиса, заменив их на настоящие. При успешном вып-нии получаем 1е допустимое решение, если нет - о ни одного доп реш нет. Сбаз А1 W1 | –М | –М W2 | - М | 0 х3 | 0 | Проверяется признак оптим, т.е считается оценки столбцов ∆1, ∆2,.. ∆4≥0 ∆1= -М*1 + (-М)*0 +0*0,2 –С1=0-М, ∆j=СбазВ-1Аj-Cj≥0, В-1 заменяется на Е –един матрицу. Первая итерация - определяется вектор А1 - кандидат на ввод в базис - имеющий максимальную по модулю отрицательную оценку (-М); кандидат на вывод из базиса - вектор W1 определился из минимума отношения компонент текущего решения к положительным элементам столбца А1 (направляющий элемент преобразования). Преобразования плана осуществляется по правилу "четырёхугольника".
Вторая итерация - определяется вектор А2 - кандидат на ввод в базис и вектор А3, удаляемый из базиса. 2 этап: Третья итерация - определяется вектор А0 - кандидат на ввод в базис и вектор W2, удаляемый из базиса. Это уже идёт оптимизация допустимого решения - первый этап завершился на второй итерации. На четвёртой итерации выясняется, что полученное решение оптимально - все оценки столбцов матрицы условий неотрицательны.
Билет 12 Билет 16 Формулировка двух типов задач поиска решений при использовании детерминированного эквивалента стохастической задачи МП на максимум математического ожидания функции цели и на максимум вероятности (надежности) достижения заданного уровня функции цели. Рассматривается задача ЛП, в которой требуется найти максимум линейной формыL=(C,X)àMAX при условиях AX≤B и X≥0, причем элементы вектора ограничений, элементы матрицы условий и коэффициенты функции цели могут быть случайными числами как с известными характеристиками (случай риска), так и неизвестными (случай неопределенности). 1) все значения заменяются на мат. ожидании (среднее значение) – максимизация результата при заданной надежности P ≥ Р при Fà max Случаен только вектор С функции цели, остальная информация детерминирована. Обычный в этой ситуации подход - выбор в качестве критерия математического ожидания функции цели - сводит задачу к детерминированной (критерий имеет вид (^C,X)àMAX, где ~С - математическое ожидание вектора С). Если статистические характеристики вектора С неизвестны, то применяются различные гипотезы и оценки, а также методы анализа зоны неопределенности. 2) максимизация надежности при заданном уровне эффекта F ≥ F при maxP(F). Если случайны не только вектор С, но и другая информация: вектор В и матрица условий А, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений. Р(SUM Aij*Xj <= Bi) >= Pi; i=1,...,m; 0 =< Pi <= 1 при этом часто матрица А предполагается фиксированной и случаен только вектор ограничений В; если множество возможных состояний природы конечно и известны характеристики (оценки значений и их вероятностей) для каждого элемента Вi (т.е. Bki и Hki для k=1,...,s), то можно определить значения ~Bi, которые удовлетворяют условию P(Bi(q)>=~Bi)>=Pi; действительно, для этого необходимо упорядочить значения Bki в порядке убывания и выбрать наименьшую группу, удовлетворяющую условию: вероятность попадания значения Bi в данную группу больше или равна Pi (для этого суммарная вероятность группы должна быть больше или равна Pi). Тогда задача будет сведена к детерминированной: (^C,X)àMAX AX<=~B, где ~B=(~B1,~B2,...,~Bm)
Билет 17 Билета 18 Билет 20 Билет 23 Билет 25 Билет 26 Содержание процесса моделирования и его отдельных этапов, их взаимосвязь. Классификация моделей. Основные элементы экономико-математической модели. Модель -объект-заместитель,который отражает существенные характеристики оригинала т.е.,изучая модель мы получаем нов.знания об оригинале. ОригиналàмодельàЭММàОригинал Физическая модель (самолета, солнечной системы) МОДЕЛИРОВАНИЕ-необходимо для косвеного опосредованного изучения объекта. Типовые экономические модели:МАКРОМОДЕЛИ 1)модель народонаселения(демографич.)(труд.ресрсы с учетом миграции,пола…) 2)отраслевые модели(топливная,э/энергетика,транспортная система) 3)модели Римского Клуба(перспективы цивилизации) МЕЗОМОДЕЛИ(средний уровень):1)все субъекты РФ 2)области,республики,края,округа 3)предприятия,объединения(корпорации)(кроме ТНК). 4)города,районы. Расчеты можно проводить на всех уровнях(например МОБ).
Билет 27 Билет 28 Основные направления исследований по экономико-математическому моделированию (ЭММ). Современные сферы использования ЭММ в экономических исследованиях, множественность соответствующих прикладных дисциплин. ЭММ: экон кибернетика, систем анализ, теория принятия реш, эконометрика, статистика. Затруднения при изучении ЭММ. Для полноценного изучения необходимы знания, с одной стороны: математического анализа, особенно дифференциального исчисления; высшей, особенно линейной и матричной алгебры; математического программирования (методов оптимизации); теории вероятностей и математической статистики; с другой стороны: основ экономической теории (макро- и микроэкономики); экономической статистики; различных разделов конкретной экономики (народного хозяйства, регионов, отраслей и предприятий).
Билет 29 Показатели экономики на макроуровне и их взаимосвязь в межотраслевом разрезе. Схема, система показателей и важнейшие соотношения межотраслевого баланса (МОБ). МОБ
Свойства матрицы А:1).(Aij)<1;2).Σaij<1(для правильной матрицы);3).Матрица А д.б. продуктивной и не содержать циклов(все отрасли между собой обязательно взаимосвязаны). Продуктивность( при люб.заданном векторе конечной продукции Y всегда существует вектор валовой продукции Х,при котором решение системы уравнений существует). Х=А*Х – вектор валовой продукции;+Y-вектор конечной продукции;+S-сальдо ввоза-вывоза. Х(Е-А)=Y’;Е-единичная конечная матрица;Y’-скорректированная конечная продукция с учетом ввоза-вывоза .(Е-А)-1(Е-А)Х=Y(Е-А)-1àЕХ=Х=Y(Е-А)-1; (Е-А)-1=С -вектор(матрица)полных затрат(учитывает все прямые и косвенные затраты). Х=С*Y’. ЦЕЛЬ: Определить валовую продукцию каждой отрасли,при которых достигается заданный объем конечной продукции и одновременно одновременно оптимизировать некоторый критерий F(экономический).F1-min суммарных приведенных затрат (производственных критерий). F1àminΣcjxj – затраты будущих периодов.(1+Е)-t, t=1,2,3,4,5(лет)F2-max Yнпн(непроизв.потреб и накопленà)(социальный критерий) F3-min выбросы(экологический критерий) F3àminΣμisXj, μis -приведенная масса выбросов.ОГРАНИЧЕНИЯ:1).на невозобновляемые прир.ресурсы ΣqjrXj=<Qr, r=1,…k;2).по приросту мощностей.РЕЗУЛЬТАТ:1).оптимальный объем продукции для каждой отрасли Х1*,Х2*…Хn* при заданном Y и F*(F2*,F3*);2).материально-вещественные потоки(связи)между отраслями;3).удельные показатели для сравнения с мировыми(энергоёмкость,трудоемкость).
Билет 33 Билет 34 МОБ
Свойства матрицы А:1).(Aij)<1;2).Σaij<1(для правильной матрицы);3).Матрица А д.б. продуктивной и не содержать циклов(все отрасли между собой обязательно взаимосвязаны). Продуктивность( при люб.заданном векторе конечной продукции Y всегда существует вектор валовой продукции Х,при котором решение системы уравнений существует). Х=А*Х – вектор валовой продукции;+Y-вектор конечной продукции;+S-сальдо ввоза-вывоза. Х(Е-А)=Y’;Е-единичная конечная матрица;Y’-скорректированная конечная продукция с учетом ввоза-вывоза .(Е-А)-1(Е-А)Х=Y(Е-А)-1àЕХ=Х=Y(Е-А)-1; (Е-А)-1=С -вектор(матрица)полных затрат(учитывает все прямые и косвенные затраты). Х=С*Y’. ЦЕЛЬ: Определить валовую продукцию каждой отрасли,при которых достигается заданный объем конечной продукции и одновременно одновременно оптимизировать некоторый критерий F(экономический).F1-min суммарных приведенных затрат (производственных критерий). F1àminΣcjxj – затраты будущих периодов.(1+Е)-t, t=1,2,3,4,5(лет)F2-max Yнпн(непроизв.потреб и накопленà)(социальный критерий) F3-min выбросы(экологический критерий) F3àminΣμisXj, μis -приведенная масса выбросов.ОГРАНИЧЕНИЯ:1).на невозобновляемые прир.ресурсы ΣqjrXj=<Qr, r=1,…k;2).по приросту мощностей.РЕЗУЛЬТАТ:1).оптимальный объем продукции для каждой отрасли Х1*,Х2*…Хn* при заданном Y и F*(F2*,F3*);2).материально-вещественные потоки(связи)между отраслями;3).удельные показатели для сравнения с мировыми(энергоёмкость,трудоемкость).
Билет 35 Содержание общей проблемы оценки надежности решений задач МП. Понятие областей устойчивости
Билет 30 график добавить Билет 33 график Билет 35 график Билет №1 Практика и теория поиска лучших решений. Структуризация эко-ких задач. Си-ма – совоку-ть взамосвязанных эл-тов, обладающая определенной целостностью (относительной изолированностью от вн. среды) и присущей целью развития. Бывают: простые и сложные, большие и малые. Сложность си-мы зависит от доступности инф-ции по упра-нию этой си-мой. Си-ма простая, если есть инф-ция доступная и достаточная для упра-ния. Иначе – сложная. Модель- исп-тся для целец познания объектов и процессов. Пример:объект- земной шар, мо-ли – глобус,карта. Мо-ль- заме-тель оригинала, отража-ий его хара-ки, существенные с позиции упра-ния, т.о. что изучение мо-ли дает новые сведения об оригинале. Отл от др инструментов тем, что они ориенти-ны на косвенное изучение. Класифи-ция моделей: физ-кие и абстрактыне, реальные и символьные, образные и словестные. ЭМ мо-ль – отражение упра-мого объекта с помощью мат соотно-ний(инструментов). ЭМ мо-ли: лин-ые и нели-ные, непрерывные и дискретные, простран-ные и точечные. Реальные мо-ли хар-тся стохастичностью (неопре-ый хар-тер). Математическое программирование ("планирование")– это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Эк-мат классиф моделей: 1. По типу мат описания – линейное и Нелинейное; 2. геометрические, выпуклые, Целочисленные (дискретные –переменные только целые), Стохастические, Динамические (время учит-ся явным образом); 3. Точечные (EX. Прибыль за год), Пространствен (Ex.логистика - отраж простран аспекты). Линейное программирование (ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие: 1) показатель оптимальности L(X) представляет собой линейную функцию от элементов решения X=(x1,x2,…,xn); 2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. Билет № 2 Компромиссный критерий Гурвица и его истолкование. Проблема выбора параметров критерия. Это компромисс между крайним пессимизмом и умеренным оптимизмом. 0≤α≤1, α – степень пессимизма оперирующей стороны. 1 – пессимист, 0 – оптимист. H = αmax i(minj aij) (пессимист)+ (1-α)max i(minj aij). H =max[α minj aij + (1-α)maxj aij]. –критерий Гурвица.
Билет №3 Задача математического программирования (МП) и ее свойства. Классификация задач МП. Математическое программирование ("планирование")– это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так распределительных задач. Анализируемые процессы считаются многократно повторяющимися и следовательно ими можно управлять. 1. Мат. программирование – один из разделов математики, который изучает методы нахождения условного экстремума ф-ии многих переменных. Разделы мат. программирования: 1) линейное программирование: f(x) стремится min(max), x принадлежит X. целевая ф-ия явл. линейной, а множ-во Х задается системой лин-х равенств и неравенств; 2) нелинейное программирование: а) выпуклое программирование. Относятся задачи на отыскание min-ма ф-ии если мн-во Х выпукло и целевая ф-ия выпукла тоже. min на выпуклом U, max на вогнутом ∩. б) задачи квадратичного программирования, где целевая ф-ия квадратична, а ограничения – линейны. в) многоэкстремальная задача. 3) целочисленное программирование – задачи ЛП при условии что все переменные или некоторые из них явл. целочисленными. Особенности задач МП: 1) классические методы отыскания усл. экстремума ф-ии не работают из-за ограничений типа неравенства; 2) из-за большой размерности задач и большого числа ограничений, проверить все потенциальные экстремальные точки не. Цели МП: создание аналитических методов опр-ия решения, а в случае если это невозможно, то создание эф-х вычислит-х способов получения приближенного решения. Этапы построения мат. моделей: 1) построение качественной модели рассматриваемой задачи (опр-ть все факторы, которые оказывают влияние, установить закономерности которые наиболее значимы); 2) запись с помощью мат. знаков построенной кач. модели (выделение управляющих и управляемых факторов); 3) исследование влияния переменных на значение целевой ф-ии; 4) непосредственное решение поставленной задачи и проверка адекватности модели. Билет № 4
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.179.238 (0.017 с.) |

 -оцениваем доход, но является ненадежной(оценка весьма приближенная);Найдем Хопт без ЕИЭ.2ШАГ:ориентируемся на ситуацию с наибольшей вероятностью.Предположим,что это П1.Найдем доход мах в столбце П1,это L1=>выберем стратегию с мах доходом.Если П2àL2,…ПnàLn.Оцениваем средний доход при проведении ЕИЭ:
-оцениваем доход, но является ненадежной(оценка весьма приближенная);Найдем Хопт без ЕИЭ.2ШАГ:ориентируемся на ситуацию с наибольшей вероятностью.Предположим,что это П1.Найдем доход мах в столбце П1,это L1=>выберем стратегию с мах доходом.Если П2àL2,…ПnàLn.Оцениваем средний доход при проведении ЕИЭ:  ;3ШАГ: аэкспср-амахср=аэк.доход;4ШАГ: аэксп.эфф=(аэк.дох-С(затраты))/С; 5ШАГ:необходимо сравнить аэксп.эфф с внутренней нормой прибыли.Если аэксп.эфф>=IRR, то целесообразно применить ЕИЭ, аэксп.эфф<IRR -применяется метод компромиса с учетом риска.Если ЕИЭ целесообразен, то Затраты д.б.<min ср.риска!
;3ШАГ: аэкспср-амахср=аэк.доход;4ШАГ: аэксп.эфф=(аэк.дох-С(затраты))/С; 5ШАГ:необходимо сравнить аэксп.эфф с внутренней нормой прибыли.Если аэксп.эфф>=IRR, то целесообразно применить ЕИЭ, аэксп.эфф<IRR -применяется метод компромиса с учетом риска.Если ЕИЭ целесообразен, то Затраты д.б.<min ср.риска! (искомый вектор)
(искомый вектор)
 В стохастической модели необходимо оценивать попадание случайной величины в определенный диапазон, чтобы знать значение цели. Для этого используют график кумулятивы:
В стохастической модели необходимо оценивать попадание случайной величины в определенный диапазон, чтобы знать значение цели. Для этого используют график кумулятивы: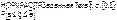


 i=1,…n,-отрасли хозяйства,Хi-валовая продукция;j=1,…n-потребление отрасли.А-матрица прямых производственных затрат(квадратная матрица);aij-затраты вал.продукции i на единицу объема выпуска отрасли j.Y-конечная продукция(выходит за рамки производственого процесса). Y=Yамортизация(нокопление)+Yкап.вложения на расширение+Yнепрофил.потр-ие и накопл+Yзапасы;Х1=а11Х1+а12Х2+…+а1nХn – прямое производственное потребление; Х1+Y1 =баланс при замкнутой системе; Х1+Y1+Sвывоз-Sввоз,S+,S-=S1-сальдо ввоза вывоза. Произв-ая функция Леонтьева:
i=1,…n,-отрасли хозяйства,Хi-валовая продукция;j=1,…n-потребление отрасли.А-матрица прямых производственных затрат(квадратная матрица);aij-затраты вал.продукции i на единицу объема выпуска отрасли j.Y-конечная продукция(выходит за рамки производственого процесса). Y=Yамортизация(нокопление)+Yкап.вложения на расширение+Yнепрофил.потр-ие и накопл+Yзапасы;Х1=а11Х1+а12Х2+…+а1nХn – прямое производственное потребление; Х1+Y1 =баланс при замкнутой системе; Х1+Y1+Sвывоз-Sввоз,S+,S-=S1-сальдо ввоза вывоза. Произв-ая функция Леонтьева:  .
. i=1,…n,-отрасли хозяйства,Хi-валовая продукция;j=1,…n-потребление отрасли.А-матрица прямых производственных затрат(квадратная матрица);aij-затраты вал.продукции i на единицу объема выпуска отрасли j.Y-конечная продукция(выходит за рамки производственого процесса). Y=Yамортизация(нокопление)+Yкап.вложения на расширение+Yнепрофил.потр-ие и накопл+Yзапасы;Х1=а11Х1+а12Х2+…+а1nХn – прямое производственное потребление; Х1+Y1 =баланс при замкнутой системе; Х1+Y1+Sвывоз-Sввоз,S+,S-=S1-сальдо ввоза вывоза. Произв-ая функция Леонтьева:
i=1,…n,-отрасли хозяйства,Хi-валовая продукция;j=1,…n-потребление отрасли.А-матрица прямых производственных затрат(квадратная матрица);aij-затраты вал.продукции i на единицу объема выпуска отрасли j.Y-конечная продукция(выходит за рамки производственого процесса). Y=Yамортизация(нокопление)+Yкап.вложения на расширение+Yнепрофил.потр-ие и накопл+Yзапасы;Х1=а11Х1+а12Х2+…+а1nХn – прямое производственное потребление; Х1+Y1 =баланс при замкнутой системе; Х1+Y1+Sвывоз-Sввоз,S+,S-=S1-сальдо ввоза вывоза. Произв-ая функция Леонтьева: 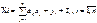 .
.


