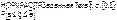Возможные исходы при решении задач ЛП

1. нет ни одного решения (это значит что условие 2 и 3 противоречивы). Оказалось что направленный перебор вершин эффективен (по градиенту). Этот метод назван симплекс методом. Оптимальным называется решение лучше которого при заданных условиях не существует. Это решение обознач Х*. F*=F(C,X*)≥F(C,X).

2. Если доп мн-во огранич (замкнуто) реш задачи сущ-ет и на min и на max, т.е сущ-ет оптим реш.

3. Задача на max разрешима, а на min функция целей неограниченна.

4. Реш на min сущ-ет, а на maxФЦ неоганиченна.

Блок схема симплекс метода: 1. Поиск первой доп вершины → если да → 2. хар-ка текущ реш → 3.проверка оптимальности → если да → то 4.анализ рез-тов, → если нет →то 5.поиск ближайшей лучшей вершины → если нет, →то 6. критерий не огранич, → если да →то 2.хар-ка текущего решения.

Один такой шаг называется итерацией.

Теорема. Метод является конечным если не возникает зацикливаний из-за потери точности счета. Существуют специальные в т.ч. автоматизированные условия выхода из цикла.

Кол-во столбцов n не влияет не на число шагов, а на трудоемкость каждого отдельного шага.

Опр: Решения, соответствующие вершинам называют опорными (базисными). Для оптимального решения так же как для базисного. B(MxM) Матрица В называется базисной. Для каждой вершины она своя. Эта матрица не вырождена, для нее всегда существует обратная, значит ее определитель отличен от нуля, вместо А можем подставить ВХ=b. BX=b|B^-1;X=B^-1*BX =b^-1b;EX=B^-1b; X=B^-1b Предполагалось что ранг матрицы А равен m. Это значит что все столбцы линейно независимы. Все столбцы не входящие в базисную матрицу могут быть представлены как неотрицательные комбинации столбцов Ak=α₁А1+ α₂A2+…

Св-ва СМ:

1. конечное число шагов

2. если менять местами столбцы или строки, то реш не изменится.

3. Если к условиям модели добавить одну или несколько строк, являющихся комбинациями уже существующих, то реш задачи не изменится. Доп условия б избыточны.

∆ - оценки рентаб-ти произв-х способов = оценки столбцов.

Предполагаем, что задача приведена в каконическом виде.

∑cjxj→max (j=1,n), Ax=B, x≥0.

Теорема 6: Каждой вершине доп множества соответсвует определенный базис. (В таблице на первые места м ставить базисные вектора, в этом случае продукцию м перенумеровать).

Теорема 7: Для базисного решения, не обязат оптим, число положительных компонентов не превышает m.

Х баз = (х1, х2…хm | хm+1…х n)

>0 =0

 

Билет 10

Формулировка задачи выбора решений в виде задачи математического программирования (МП) с прямым заданием стохастичности условий.

Рассматривается задача ЛП, в которой требуется найти максимум линейной формы (искомый вектор)

Входная информация (детерминированная – однозначно задана) не точная, приближенная, характеризуется неопределенностью

Экспертная оценка все-равно используется: 1) средне наибольшая вероятность – оценка математического ожидания (все случайные величины – ξ); 2) коэффициент вариации Кв (NPV)

В стохастической модели необходимо оценивать попадание случайной величины в определенный диапазон, чтобы знать значение цели. Для этого используют график кумулятивы:

 

 

искомое решение

 

 

-3ξ ξ ξ1 ξ2 +3ξ

График показывает поведение функции цели как случайной величины не зависимо от количества ресурсов. Вероятностный характер имеет и функция цели (цены) и коэффициенты расхода ресурса (их возможного недостатка). Ресурсы детерминированы, случайной компоненты нет, функция цели – стох.

Используется норм. распределение: НОРМРАСПР (заданная точка; ξ; σ; [0,1])

Р – надежность рез-та (попадание ф-ии цели в правый хвост от задан. гр-цы.

Решение: 1) все значения заменяются на мат. ожидании (среднее значение) – максимизация результата при заданной надежности P ≥ Р при Fà max; 2) максимизация надежности при заданном уровне эффекта F ≥ F при maxP(F)

Обычно проводят серию расчетов при различных коэффициентах вариации и при различных требованиях к надежности выполнения рес-ных обязательств.

Следует ожидать, что с ростом неопределенности и требований к надежности результаты снизятся, т.к. значительная часть ресурсов будет отвлекаться в резервы.

Недостаток – не можем сказать, с какой вер-тью получилась функция цели.

F(x)àmax – случайная величина, распределенная по нормальному закону (можно подсчитать все ее параметры).

В постановках стох. задач рассматривают следующие пок-ли кач-ва решений:

- математическое ожидание линейной формы (функции цели);

- дисперсия функции цели;

- лин. комбинация (компромисс) мат. ожидания и дисперсии ф-ии цели;

- вероятность превышения функцией цели некоторого фиксированного порога;

- математическое ожидание полезности функции цели;

- максимин функции цели (или математического ожидания функции цели).

 

Билет 11

Содержание двух этапов симплекс-процесса и основные характеристик соответствующих процедур.

На предприятии производят два вида продукции - А и Б. Для выпуска единицы продукции А требуется 0.2 ед. труда; Б - 0.4 ед. труда и 0.1 ед. продукции а.

Формализация задачи в виде модели ЛП:

Найти максимум Х0 при условиях

X1 - 0.1X2 = 0.75X0

X2 = 0.25X0

0.2X1 + 0.4X2 + X3 = 100

X=(X1,X2,X3)>=0

Здесь Х0 - валовый выпуск продукции в стоимостном выражении; Х1 и Х2 выпуск продукции А и Б соответственно; Х3 - дополнительная переменна имеющая смысл неизрасходованного труда (резерв рабочего времени). Расширенная задача с включением искусственных переменных для создания единич исходного базиса:

Найти максимум Х0-МW1-MW2 при условиях

X1 - 0.1X2 - 0.75X0 + W1 = 0

X2 - 0.25X0 + W2 = 0

0.2X1 + 0.4X2 + X3 = 100

X = (X1,X2,X3) >= 0

Смысл условий: первое условие есть баланс выпуска и расхода продукции А; второе условие учитывает при выпуске продукции Б расход промежуточного продукта А; третье условие есть баланс рабочего времени (труда). Коэффициенты разложения по базису W1, W2, X3 векторов-столбцов матрицы услов совпадают с самой матрицей, ибо базис - единичная матрица.

1 этап: в соответствии с алгоритмом осущ-ся исключение искусств переменных W1 и W2 из базиса, заменив их на настоящие. При успешном вып-нии получаем 1е допустимое решение, если нет - о ни одного доп реш нет.

Сбаз А1

W1 | –М | –М W2 | - М | 0 х3 | 0 |

Проверяется признак оптим, т.е считается оценки столбцов ∆1, ∆2,.. ∆4≥0

∆1= -М*1 + (-М)*0 +0*0,2 –С1=0-М,

∆j=С_базВ^-1А_j-C_j≥0, В^-1 заменяется на Е –един матрицу.

Первая итерация - определяется вектор А1 - кандидат на ввод в базис - имеющий максимальную по модулю отрицательную оценку (-М); кандидат на вывод из базиса - вектор W1 определился из минимума отношения компонент текущего решения к положительным элементам столбца А1 (направляющий элемент преобразования). Преобразования плана осуществляется по правилу "четырёхугольника".

Вторая итерация - определяется вектор А2 - кандидат на ввод в базис и вектор А3, удаляемый из базиса.

2 этап:

Третья итерация - определяется вектор А0 - кандидат на ввод в базис и вектор W2, удаляемый из базиса. Это уже идёт оптимизация допустимого решения - первый этап завершился на второй итерации.

На четвёртой итерации выясняется, что полученное решение оптимально - все оценки столбцов матрицы условий неотрицательны.

 

Билет 12