
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача ЛП с параметрами в правых частях ограничений, свойства решающей функции и множества разрешимости.Содержание книги
Поиск на нашем сайте
1) Функция цели Цены bi’+μbi” i=1,m
Теорема. Область представляет собой связанное множество относительно параметра. Область является связанной и состоит из конечного числа локальных областей устойчивости. Область не разрешима, если она представляет собой луч с выколотым началом. Теорема: Алгоритм симплекс-типа со специальными правилами перехода от текущего базиса к следующему позволяет полностью исследовать модель за конечное число шагов при условии, что предпринимаются меры против зацикливания процессов. 2) Функция цели: Цены bi’+tbi” i=1,m
Теорема. Область представляет собой связанное множество относительно параметра. Область является связанной и состоит из конечного числа локальных областей устойчивости. Область не разрешима, если она представляет собой луч с выколотым началом. Теорема: Алгоритм симплекс-типа со специальными правилами перехода от текущего базиса к следующему позволяет полностью исследовать модель за конечное число шагов при условии, что предпринимаются меры против зацикливания процессов. Теорема: функция может быть линейной либо второго порядка в области разрешимости. F(x,t)=F0+F1t+F2t2 Типы моделей, для которых используются строгие эффективные методы: 1) Функция цели зависит от λ – PARAOBJ, F(x, λ) 2) Функция цели зависит от параметра b’+μb” – PARARHS 3) зависимость от t 4) два различных параметра – λ и μ 5) Любая строка матрицы условий зависит от параметра PARAROW (параметры вводятся только в строки) (ai1*+µai1**) -1й элемент (аi2*+µаi2**) – 2й элемент 0≤µ≤µ - количественный параметр аi2* - коэф-т расхода сырья аi2** - темпы изменения по линейному закону 6) Любой столбец зависит от параметра PARACOL (столбцы условий) Когда вводятся параметры в столбцы. Третий случай – когда добавляются ещё цены реализации 0≤t≤t’ Функция второго порядка F(t)=F*+tF**+t²F*** Цены меняются вне зависимости от запасов на складе – двухпараметрическая модель Билет 34 Линейная модель межотраслевого баланса и типовые задачи. Информационные основы расчетов. МОБ
Свойства матрицы А:1).(Aij)<1;2).Σaij<1(для правильной матрицы);3).Матрица А д.б. продуктивной и не содержать циклов(все отрасли между собой обязательно взаимосвязаны). Продуктивность( при люб.заданном векторе конечной продукции Y всегда существует вектор валовой продукции Х,при котором решение системы уравнений существует). Х=А*Х – вектор валовой продукции;+Y-вектор конечной продукции;+S-сальдо ввоза-вывоза. Х(Е-А)=Y’;Е-единичная конечная матрица;Y’-скорректированная конечная продукция с учетом ввоза-вывоза .(Е-А)-1(Е-А)Х=Y(Е-А)-1àЕХ=Х=Y(Е-А)-1; (Е-А)-1=С -вектор(матрица)полных затрат(учитывает все прямые и косвенные затраты). Х=С*Y’. ЦЕЛЬ: Определить валовую продукцию каждой отрасли,при которых достигается заданный объем конечной продукции и одновременно одновременно оптимизировать некоторый критерий F(экономический).F1-min суммарных приведенных затрат (производственных критерий). F1àminΣcjxj – затраты будущих периодов.(1+Е)-t, t=1,2,3,4,5(лет)F2-max Yнпн(непроизв.потреб и накопленà)(социальный критерий) F3-min выбросы(экологический критерий) F3àminΣμisXj, μis -приведенная масса выбросов.ОГРАНИЧЕНИЯ:1).на невозобновляемые прир.ресурсы ΣqjrXj=<Qr, r=1,…k;2).по приросту мощностей.РЕЗУЛЬТАТ:1).оптимальный объем продукции для каждой отрасли Х1*,Х2*…Хn* при заданном Y и F*(F2*,F3*);2).материально-вещественные потоки(связи)между отраслями;3).удельные показатели для сравнения с мировыми(энергоёмкость,трудоемкость).
Билет 35
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.117.234 (0.009 с.) |

 -кусочно-линейная, выпуклая вверх
-кусочно-линейная, выпуклая вверх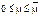 Коэффициенты монотонно убывают.
Коэффициенты монотонно убывают.

 i=1,…n,-отрасли хозяйства,Хi-валовая продукция;j=1,…n-потребление отрасли.А-матрица прямых производственных затрат(квадратная матрица);aij-затраты вал.продукции i на единицу объема выпуска отрасли j.Y-конечная продукция(выходит за рамки производственого процесса). Y=Yамортизация(нокопление)+Yкап.вложения на расширение+Yнепрофил.потр-ие и накопл+Yзапасы;Х1=а11Х1+а12Х2+…+а1nХn – прямое производственное потребление; Х1+Y1 =баланс при замкнутой системе; Х1+Y1+Sвывоз-Sввоз,S+,S-=S1-сальдо ввоза вывоза. Произв-ая функция Леонтьева:
i=1,…n,-отрасли хозяйства,Хi-валовая продукция;j=1,…n-потребление отрасли.А-матрица прямых производственных затрат(квадратная матрица);aij-затраты вал.продукции i на единицу объема выпуска отрасли j.Y-конечная продукция(выходит за рамки производственого процесса). Y=Yамортизация(нокопление)+Yкап.вложения на расширение+Yнепрофил.потр-ие и накопл+Yзапасы;Х1=а11Х1+а12Х2+…+а1nХn – прямое производственное потребление; Х1+Y1 =баланс при замкнутой системе; Х1+Y1+Sвывоз-Sввоз,S+,S-=S1-сальдо ввоза вывоза. Произв-ая функция Леонтьева: 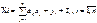 .
.


