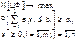Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак оптимальности решения задачи ЛП, его обоснование и экономическая интерпретация.Содержание книги
Поиск на нашем сайте
Эффективной признается такая технология для которой выполняется строгое равенство, когда значимость равна цене. Теорема: Условие оптимальности решения: ∆j =∑yiaij-Ci≥0, j=1,n т Теорема 3. Если задача ЛП разрешима, т.е. м найти max или min, то оптим множ-во содержит хотя одну вершину. (Оптим реш Х* =(х*1, …х*n), F(x*) ≥F(x), x принадл D, F – функция целей. Если реш оптим, то улучшить его при заданном условии и по задан критериям невозможно. Сов-ть оптим реш – оптим множ-во).Если решение оптимально, то условие выполняется для всех столбцов: Признак оптимальности: Ax=B, x≥0 м записать Вх=b, х=В-1 b – текущее решение. С баз = (с1, с2…с m). (5) ∆j =Сбаз В-1 Аj - Сj≥0 – требования оптим. Эконом смысл: Сбаз В-1 Аj – значимость используемых рес-сов на ед объема прод-ции; Сj –эффект от ед объема.. Суммарная значимость испол рес-сов не м б ниже эффекта, полученного от их использования. Затраты оцениваются по значимости рес-сов. Значимость зав-т от рыночных цен на рес-с, от дефицита его на предприятии, от эфф-ти его применения на данном предприятии. Одновременно рассчитывается у для каждого ресурса. Эф-ные способы, для кот продукция вып-ся только те виды, кот эф-ны, т.е. значимость = эффекту. Если условие (5) не выполняется, то решение не оптимально. ∆j=СбазВ-1Аj-Cj≥0, СбазВ-1=Y, Сбаз=1, m – рыночные цены в базисной матрице, Aj – столбец если левая граница, то правая <0, если не на границе, то 0,если правая граница то >0. Реш-е оптимально, если лучшего при заданных условиях не существует. Х* - оптимальное.
Билет 14 Схема преобразования стохастической задачи МП к эквивалентному детерминированному виду. Содержательное истолкование детерминированной задачи. Рассматривается задача ЛП, в которой требуется найти максимум линейной формы L=(C,X)àMAX при условиях AX≤B и X≥0, причем элементы вектора ограничений, элементы матрицы условий и коэффициенты функции цели могут быть случайными числами как с известными характеристиками (случай риска), так и неизвестными (случай неопред-ности). Если задача полностью стохастическая, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений. Исходной задаче может соответствовать различные определения (модели) стохастической задачи: Если случайны не только вектор С, но и другая информация: вектор В и матрица условий А, то необходимо уточнить исходную постановку задачи: определить, что понимается под допустимым решением (планом), а также смысловое содержание показателя качества решений. Решение задачи Х рассматривается как детерминированный (фиксированный) вектор; допустимым решением (планом) считается такой вектор Х, который удовлетворяет ограничениям задачи при всех возможных сочетаниях значений А и В, имеющих положительную вероятность; это жесткая постановка задачи, не использующая дополнительных сведений относительно статистических характеристик условий в модели. A(q)*X<=B(q) для всех q@Q,X>=0 Здесь q‑случайные параметры, от которых зависят значения А и В (состояния природы), их набор обычно считается конечным; Р(SUM Aij*Xj <= Bi) >= Pi; i=1,...,m; 0 =< Pi <= 1 при этом часто матрица А предполагается фиксированной и случаен только вектор ограничений В; если множество возможных состояний природы конечно и известны характеристики (оценки значений и их вероятностей) для каждого элемента Вi (т.е. Bki и Hki для k=1,...,s), то можно определить значения ~Bi, которые удовлетворяют условию P(Bi(q)>=~Bi)>=Pi; действительно, для этого необходимо упорядочить значения Bki в порядке убывания и выбрать наименьшую группу, удовлетворяющую условию: вероятность попадания значения Bi в данную группу больше или равна Pi (для этого суммарная вероятность группы должна быть больше или равна Pi). Тогда задача будет сведена к детерминированной: (^C,X)àMAX AX<=~B, где ~B=(~B1,~B2,...,~Bm) при условии жесткой постановки (одноэтапной); Нахождение решения стохастической задачи в жесткой постановке может быть организовано следующим образом: - если X - допустимый план (перманентное решение) задачи, то он удовлетворяет соотношению A^X<=B^ для любой допустимой (возможной) пары [A^,B^]. Обычный подход сводится к рассмотрению решения детерминированной задачи, полученной заменой вероятностных условий их математическими ожиданиями; после этого проверяется перманентность плана (в случае ограниченности элементов матрицы А и В это несложно)
Билет 15
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.141 (0.008 с.) |