
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретико-методическое описание метода линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики. Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. По типу решаемых задач методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов. [3, c.7] Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: 1. рационального использования сырья и материалов; 2. задачи оптимального раскроя; 3. оптимизации производственной программы предприятий; 4. оптимального размещения и концентрации производства; 5. составления оптимального плана перевозок, работы транспорта (транспортные задачи); 6. управления производственными запасами; 7. и многие другие, принадлежащие сфере оптимального планирования. Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке, задачи этого раздела выглядят следующим образом. Требуется найти такие неотрицательные
… … … … … … … … … …
В зависимости от вида функции Формы задач линейного программирования: 1. стандартная; 1.1 первая стандартная форма (формула 1.3); 1.2 вторая стандартная форма (формула 1.4); 2. каноническая (формула 1.5).
… … … … … … … … … …
… … … … … … … … … …
… … … … … … … … …
Задачу на минимум (формула 1.6) можно решать как задачу на максимум. Достаточно знаки целевой функции поменять на противоположные (формула 1.7). В результате необходимо знак целевой функции поменять на противоположный.
Аналогично можно сменить знак неравенства меньше или равно (формула 1.8) на больше или равно (формула 1.9).
Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в вершине допустимой области. Если целевая функция достигает экстремального значения более чем на одной вершине, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих вершин (альтернативный оптимум). Эта теорема имеет важнейшие значение, так как она указывает путь решения задачи линейного программирования. Совсем не надо перебирать все точки допустимой области. Достаточно перебрать вершины допустимой области, а ведь их конечное число. Кроме того, не нужно перебирать все вершины, можно этот перебор существенно сократить. Любой набор чисел Задачи линейного программирования решаются несколькими методами: 1. графический метод; 2. симплексный метод; 3. двойственность в ЛП; 4.двойственный симплексный метод. Задачи линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение невозможно. Графический метод довольно прост и нагляден. Он основан на геометрическом представлении допустимых решений задачи. Каждое из неравенств задачи ЛП определяет на координатной плоскости При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи, существует бесконечное множество решений (альтернативный оптимум); ЦФ не ограничена; область допустимых решений– единственная точка; задача не имеет решений. [3 c.55-57] Любая задача линейного программирования, независимо от вида записи, может быть приведена к стандартной и канонической форме и решена симплексным методом, который в определенном смысле является универсальным методом ЛП. Алгоритм симплекс-метода носит итерационный характер. Симплекс-метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. Алгоритмы симплекс-метода позволяют также установить, является ли задача ЛП разрешимой. Переход от одного базиса к другому позволяет находить решения почти всех задач ЛП. Определив все крайние точки, можно вычислить значения целевой функции и найти оптимальное решение. Однако для больших значений m и n это практически невозможно. [1 c.15] Алгоритм решения задачи ЛП табличным симплексом-методом состоит из следующих этапов: 1. рассчитывают и заполняют начальную симплекс-таблицу с допустимым единичным базисом, включая индексную строку. 2. находят разрешающий столбец; 3. находят разрешающую строку; 4. рассчитывают методом Жордано-Гаусса все параметры матрицы; 5. анализируют полученные данные в индексной строке. Таблицы симплекс-метода необходимо строить до тех пор, пока не будет получен оптимальный план. План будет считаться оптимальным, если в последней индексной строке симплекс-таблицы будут только нули и положительные числа. [1 c.20-22] При построении симплексного метода предполагалось, что все опорные планы невырожденные, что обеспечивало получение оптимального плана за конечное количество шагов. В случае вырожденного плана вычисления производят аналогично, но в этом случае возможен возврат к старому базису, что приводи к так называемому зацикливанию. Метод искусственного базиса применяется при наличии в ограничении знаков “равно”, “больше либо равно”, “меньше либо равно” и является модификацией табличного метода. Решение системы производится путём ввода искусственных переменных со знаком, зависящим от типа оптимума, т.е. для исключения из базиса этих переменных последние вводятся в целевую функцию с большими отрицательными коэффициентами m, а в задачи минимизации - с положительными m. Таким образом, из исходной получается новая m - задача. Если в оптимальном решении m - задачи нет искусственных переменных, это решение есть оптимальное решение исходной задачи. Если же в оптимальном решении m - задачи хоть одна из искусственных переменных будет отлична от нуля, то система ограничений исходной задачи несовместна и исходная задача неразрешима. В основу модифицированного симплекс – метода положены такие особенности линейной алгебры, которые позволяют в ходе решения задачи работать с частью матрицы ограничений. Иногда метод называют методом обратной матрицы. В процессе работы алгоритма происходит спонтанное обращение матрицы ограничений по частям, соответствующим текущим базисным векторам. Указанная способность делает весьма привлекательной машинную реализацию вычислений вследствие экономии памяти под промежуточные переменные и значительного сокращения времени счёта. Хорош для ситуаций, когда число переменных n значительно превышает число ограничений m. В целом, метод отражает традиционные черты общего подхода к решению задач линейного программирования, включающего в себя канонизацию условий задачи, расчёт симплекс-разностей, проверку условий оптимальности, принятие решений о коррекции базиса и исключение Жордана-Гаусса. Особенности заключаются в наличии двух таблиц - основной и вспомогательной, порядке их заполнения и некоторой специфичности расчётных формул. Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу, называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Сопоставляя формы записи прямой и двойственной задач, можно установить между ними следующие взаимосвязи: 1. если прямая задача является задачей максимизации, то двойственная будет задачей минимизации, и наоборот; 2. коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи; 3. свободные члены ограничений прямой задачи становятся коэффициентами целевой функции двойственной задачи; 4. матрица ограничений двойственной задачи получается путем транспортирования матрицы ограничений прямой задачи; 5. знаки неравенств в ограничениях изменяются на противоположные; 6. число ограничений прямой задачи равно числу переменных двойственной задачи, и наоборот. Виды математических моделей двойственных задач могут быть представлены в таблице (табл. 1.1).
Таблица 1.1 Виды математических моделей двойственных задач
Таким образом, прежде чем записать двойственную задачу для данной исходной, систему ограничений исходной задачи необходимо привести к соответствующему виду. [3, с.114-115] Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем для экстремальных значений линейных функций выполняется определенное соотношение (формула 1.10). Если линейная функция одной из задач не ограничена, то другая не имеет решения.
Если прямая (а значит, и двойственная) задача разрешима, то в каждой паре двойственных условий одно является свободным, а другое закрепленным. Любое из условий называется свободным, если оно выполняется как строгое неравенство хотябы для одного оптимального вектора. Условие называется закрепленным, если оно выполняется как равенство для всех оптимальных векторов. Двойственную задачу выгоднее решать, чем прямую, если в прямой задаче при малом количестве переменных имеется большое количество ограничений. [2, c 70-71] Симплексный метод позволяет наряду с получением решения прямой задачи получать и решение двойственной задачи. Этот результат и лежит в основе двойственного симплексного метода решения задачи. Суть метода состоит в таком последовательном переборе угловых точек допустимого множества Q0 двойственной задачи, при котором значение целевой функции возрастает, т. е. в применении симплексного метода к решению двойственной задачи. Будем предполагать, что задача невырождена, т. е. каждой угловой точке множества Q0 соответствует квадратная невырожденная система уравнений размерности m, матрицу которую и называют двойственным базисом прямой задачи. Вместе с тем двойственный симплекс–метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Отыскание решения задачи двойственным симплекс-методом включает в себя следующие этапы: 1. Находят псевдоплан задачи. 2. Проверяют этот псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану. 3. Выбирают разрешающую строку с помощью определения наибольшего по абсолютной величине отрицательного числа столбца вектора Р 0 и разрешающий столбец с помощью нахождения наименьшего по абсолютной величине отношения элементов (m+1)–и строки к соответствующим отрицательным элементам разрешающей строки. 4. Находят новый псевдоплан и повторяют все действия начиная со второго этапа. Двойственный симплексный метод называют также методом последовательного уточнения оценок, поскольку угловые точки задачи, возникающие при итерациях, можно рассматривать как приближенные значения точной оценки у*, т. е. как приближенные оценки влияния условий задачи на величину минимума целевой функции. [2, c.87-92] Значительная часть экономических задач, относящихся к задачам линейного программирования, требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например распределение производственных заданий между предприятиями, раскрой материалов, загрузка оборудования, распределение судов по линиям, самолетов по рейсам, а также задачи по производству неделимой продукции. Если единица составляет малую часть всего объема производства, то оптимальное решение находят обычным симплексным методом, округляя его до целых единиц, исходя из смысла задачи. В противном случае округление может привести к решению, далекому от оптимального целочисленного решения. Задача целочисленного программирования формулируется так же, как и задача линейного программирования, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами. Метод решения таких задач, предложенный Гомори, основан на симплексном методе и состоит в следующем. Симплексным методом находится оптимальный план задачи без учета условия целочисленности. Если оптимальный план целочисленный, то вычисления заканчивают; если же оптимальный план содержит хотя бы одну дробную компоненту Xi, то накладывают дополнительное ограничение, учитывающее целочисленность компонент плана, и вычисления симплексным методом продолжают до тех пор, пока либо будет найден целочисленный оптимальный план, либо доказано, что задача не имеет целочисленных оптимальных планов. [3 c.122-123] Особенно широкое распространение линейное программирование получило в экономике, так как исследование зависимостей между величинами, встречающимися во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.195 с.) |

 , которые обеспечивают максимум или минимум целевой функции (формула 1.1), которые удовлетворяют системе ограничений (формула 1.2) и не противоречат условиям неотрицательности:
, которые обеспечивают максимум или минимум целевой функции (формула 1.1), которые удовлетворяют системе ограничений (формула 1.2) и не противоречат условиям неотрицательности:  .
. (1.1)
(1.1)
 (1.2)
(1.2)
 различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что функция
различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что функция  . [1 c.11-12]
. [1 c.11-12]

 (1.3)
(1.3)


 (1.4)
(1.4)
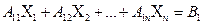
 (1.5)
(1.5)
 (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) , удовлетворяющий ограничениям задачи, называют планом, а множество всех планов допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования. [3 c.7-8]
, удовлетворяющий ограничениям задачи, называют планом, а множество всех планов допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования. [3 c.7-8] некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлен выпуклым многоугольником, неограниченным выпуклой многоугольной областью, отрезком, лучом и т.д. В случае несовместности системы ограничений задачи ОДР является пустым множеством.
некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлен выпуклым многоугольником, неограниченным выпуклой многоугольной областью, отрезком, лучом и т.д. В случае несовместности системы ограничений задачи ОДР является пустым множеством.


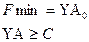
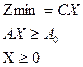



 (1.10)
(1.10)


