
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация технологических системСодержание книги Поиск на нашем сайте
В.Н. Костин
Пример оформления курсовой работы
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Факультет информационных технологий
Кафедра программного обеспечения вычислительной техники и автоматизированных систем
КУРСОВАЯ РАБОТА по курсу «Оптимизация технологических систем»
Решение задачи линейного программирования по оптимизации плана производства с целью получения максимума прибыли
ГОУ ОГУ 230100.65.6011.10 О
Руководитель работы _____________Костин В.Н. «___»______________2011г. Исполнитель студент гр. 11 ИВТ(м)ИПО _____________Кунафина Н.З. «___»______________2011г.
Оренбург 2011 Содержание Введение………………………………………………………………………………. 3 Постановка задачи……………………………………………………………………. 4 1. Теоретико-методическое описание метода линейного программирования…… 5 2. Области применения и ограничения использования линейного программирования для решения экономических задач………………………………………… 12 3. Оптимизация прибыли с применением метода ЛП……………………………. 16 3.1 Постановка задачи и формирование оптимизационной модели……………... 16 3.2 Расчет и анализ результатов оптимизации прибыли………………………. 16 4 Разработка программы……………………………………………………………. 19 4.1 Инструментальные средства, используемые при разработке………………... 19 4.2 Описание основных процедур и функций……………………………………. 19 Заключение………………………………………………………………………….. 21 Список литературы…………………………………………………………………. 22 Приложение А……………………………………………………………………….. 23
Введение Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, углублением общественного разделения труда, предъявлением высоких требований к методам планирования и хозяйственного руководства. В этих условиях только научный подход к руководству экономической жизнью общества позволит обеспечить высокие темпы развития народного хозяйства.
Одним из необходимых условий дальнейшего развития экономической науки является применение точных методов количественного анализа, широкое использование математики. В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение в экономических исследованиях и планировании. Этому способствует развитие таких разделов математики, как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники. Уже накоплен достаточный опыт постановки и решения экономических задач с помощью математических методов. Особенно успешно развиваются методы оптимального планирования, которые и составляют сущность математического программирования. Одной из основных становится задача создания единой системы оптимального планирования и управления народным хозяйством на базе широкого применения математических методов и электронно-вычислительной техники в экономике. Цель курсовой работы: 1. закрепить теоретические знания в области теории методов оптимизации, формирования алгоритмов, написания программ; 2. формирование практических умений в построении алгоритмов и написании программ, реализующих расчетный алгоритм; 3. закрепление практических навыков самостоятельного решения инженерных задач и умений анализировать полученные результаты и делать выводы. Основной целью написания курсовой работы является всесторонний анализ применения линейного программирования для решения задач в сфере электронной коммерции. Задачами курсовой работы являются: 1. Теоретико-методическое описание метода линейного программирования; 2. Выявление области применения и ограничения использования линейного программирования для решения экономических задач в сфере электронной коммерции; 3. Максимизация прибыли посредством использования методов оптимизации для отыскания путей решения данной задачи; 4. Постановка задачи и формирование оптимизационной модели; 5. Расчет и анализ результатов оптимизации прибыли. На современном этапе развития экономики не одна сфера или составная часть производства не может обойтись без оптимизации процессов. Не является здесь исключением и получение максимальной прибыли. Более того, именно получение максимальной прибыли является одной из центральных задач в ведении бизнеса.
Базой для выполнения курсового проекта является дисциплина «Оптимизация технологических систем».
Постановка задачи
В ходе курсового проекта необходимо разработать программный продукт, решающий задачи линейного программирования по оптимизации прибыли (на максимум).
Разработка программы 4.1 Инструментальные средства, используемые при разработке Прежде, чем приступить к разработке программы для реализации метода оптимизации в сфере коммерции необходимо помимо выбора алгоритма выбрать инструментальные средства для реализации и определить оптимальные параметры процедур алгоритма. Затем процедуры должны быть реализованы в виде программных модулей. С практической точки зрения представляется наиболее целесообразным проводить выше указанные исследования с использованием среды разработки программных средств Borland Delphi 7.
4.2 Описание основных процедур и функций
Для начала работы программы необходимо задать количество уравнений. Для этого в программе реализована процедура выбора файла: procedure TForm1.Button3Click(Sender: TObject); Данная процедура позволяет выбрать количество. При этом открывается диалоговое окно с каталогом. При работе программы могут возникать ситуации, когда пользователь некорректно вводит данные либо выбирает файл, неудовлетворяющий условиям, для того чтобы предупредить пользователя об этом использовались сообщения, которые реализуются посредством процедуры: procedure Error(Msg: string; Args: array of const); которая Генерирует исключительную ситуация с сообщением Msg Создает массив ссылок Regions на регионы procedure Create; Создает массив 2-мерный случайных чисел Окно интерфейса пользователя выглядит следующим образом:
Рисунок 1 – Окно интерфейса пользователя
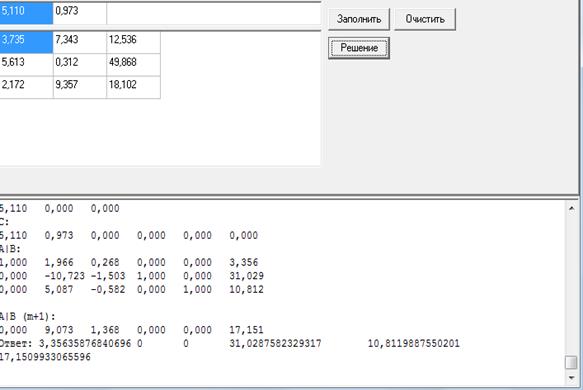
На рисунке 2 представлен результат работы программы
Рисунок 2 – Результат работы программы
Заключение Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). Математическое программирование является одним из разделов науки об исследовании операций. Задачи математического программирования находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий (программ действий), например, при решении проблем управления и планирования производственных процессов, в проектировании и перспективном планировании, в военном деле и т.д. Значительное число задач, возникающих в обществе, связано с управляемыми явлениями, т.е. с явлениями, регулируемыми на основе сознательно принимаемых решений. При том ограниченном объеме информации, который был доступен на ранних этапах развития общества, принималось оптимальное в некотором смысле решение на основании интуиции и опыта, а затем, с возрастанием объема информации об изучаемом явлении, - с помощью ряда прямых расчетов. Так происходило, например, создание календарных планов работы промышленных предприятий.
Совершенно иная картина возникает на современном промышленном предприятии с многосерийным и многономенклатурным производством, когда объем входной информации столь велик, что его обработка с целью принятия определенного решения невозможна без применения компьютеров. Еще большие трудности возникают в связи с задачей о принятии наилучшего решения. Проблема принятия решений в исследовании операций неразрывно связана с процессом моделирования. Первый этап процесса моделирования состоит в построении качественной модели. Второй этап - построение математической модели paccматриваемой проблемы. Этот этап включает также построение целевой функции, т. е. такой числовой характеристики, большему (или меньшему) значению которой соответствует лучшая ситуация с точки зрения принимающего решения. Итак, в результате этих двух этапов формируется соответствующая математическая задача. Третий этап - исследование влияния переменных на значение целевой функции. Этот этап предусматривает владение математическим аппаратом для решения математических задач, возникающих на втором этапе процесса принятия решения. Четвертый этап - сопоставление результатов вычислений, полученных на третьем этапе, с моделируемым объектом, т. е. экспертная проверка результатов (критерий практики). Таким образом, на этом этапе устанавливается степень адекватности модели и моделируемого объекта в пределах точности исходной информации. Широкий класс задач управления составляют такие экстремальные задачи, в математических моделях которых условия на переменные задаются равенствами и неравенствами. Теория и методы решения этих задач как раз и составляют содержание математического программирования. Приложение А program SimplexMethod; {$APPTYPE CONSOLE} Uses SysUtils, MatrixIO in 'matrixio.pas'; procedure Exclude(matrix: TMatrix; n,m: integer); var i,j: integer; t: extended; Begin for j:= 0 to leny(matrix)-1 do begin if j = m then continue; t:= matrix[n,j]; for i:= 0 to lenx(matrix)-1 do matrix[i,j]:= matrix[i,j] - matrix[i,m]*t; end; end; function simplex(c: TArray; ogr: TMatrix): TArray; var i,j,t,imin,jmin: integer; tt: double; a: TMatrix; cd,d,m1,res: TArray; Begin t:= Length(c); SetLength(c,t+leny(ogr)); for i:= t to leny(ogr)-1 do c[i]:= 0; SetLength(a,lenx(ogr)+leny(ogr),leny(ogr)); for j:= 0 to leny(a)-1 do for i:= 0 to lenx(a)-1 do if i < lenx(ogr)-1 then a[i,j]:= ogr[i,j] else if i = j+lenx(ogr)-1 then a[i,j]:= 1 else if i = lenx(a)-1 then a[i,j]:= ogr[lenx(ogr)-1,j] else a[i,j]:= 0; SetLength(m1,lenx(a)); SetLength(d,leny(a)); for i:= 0 to Length(d)-1 do d[i]:= i + leny(a)-1; SetLength(cd,leny(a)); Repeat for i:= 0 to Length(cd)-1 do cd[i]:= c[round(d[i])]; Writeln('c'); WriteArray(c); Writeln('a'); WriteMatrix(a); Writeln('d'); WriteArray(d); Writeln('cd'); WriteArray(cd); for i:= 0 to Length(m1)-1 do begin m1[i]:= 0; for j:= 0 to Length(m1)-1 do m1[i]:= m1[i] + cd[j] * a[i,j];
m1[i]:= m1[i] - c[i]; end; WriteLn('m1'); WriteArray(m1); for i:= 0 to Length(m1)-1 do if m1[i] < 0 then break; if not (m1[i] < 0) then break; imin:= 0; for i:= 1 to length(m1)-1 do if m1[i] < m1[imin] then imin:= i; jmin:= 0; for j:= 1 to leny(a)-1 do if not (a[imin,j] = 0) then if a[lenx(a)-1,j] / a[imin,j] < a[lenx(a)-1,jmin] / a[imin,jmin] then jmin:= j; tt:= a[imin,jmin]; d[jmin]:= imin; cd[jmin]:= c[jmin+t]; for i:= 0 to lenx(a)-1 do a[i,jmin]:= a[i,jmin] / tt; Exclude(a,imin,jmin); until false; SetLength(res,lenx(a)); for i:= 0 to Length(res)-1 do res[i]:= 0; for i:= 0 to Length(d)-1 do res[round(d[i])]:= a[lenx(a)-1,i]; res[lenx(a)-1]:= m1[length(m1)-1]; simplex:= res; end; var fun,t: TArray; ogr: TMatrix; i: integer; Begin ReadArray(fun); WriteArray(fun); ReadMatrix(ogr); WriteMatrix(ogr); t:= simplex(fun,ogr); for i:= 0 to length(t)-1 do write(t[i]:8:4); writeln;
Оптимизация технологических систем
1. Тема и цель курсовой работы
Тема курсовой работы: Оптимизация различных технологических систем с использованием методов оптимизации. Цель курсовой работы: - закрепить теоретические знания в области теории методов оптимизации, формирования алгоритмов, написания программ; - формирование практических умений в построении алгоритмов и написании программ, реализующих расчетный алгоритм; - закрепление практических навыков самостоятельного решения инженерных задач, развитие творческих способностей студентов и умений анализировать полученные результаты и делать выводы.
2. Основы теории оптимизации технологических систем изложены в учебном пособии «Математическое программирование» 3. Исходные данные к работе согласно заданию варианта. 4. Содержание расчетно-пояснительной записки: - титульный лист; - задание на курсовую работу; - формализация задачи; - решение задачи; - разработка алгоритма; - разработка программы и решение задачи; - выводы и заключение; - список используемой литературы. 5. Материалы, представляемые к защите: - расчетно-пояснительная записка; - алгоритм и программа решения задачи.
ТЕМА 1. Решение задачи линейного программирования по оптимизации плана производства с целью получения максимума прибыли (на максимум).
Цех выпускает трансформаторы двух видов. На один трансформатор 1-го вида расходуется 5 кг железа и 3 кг проволоки, а на один трансформатор 2-го вида - 3 кг железа и 2 кг проволоки. От реализации одного трансформатора 1-го вида цех получает 1,2 р. прибыли, а от реализаций одного трансформатора 2-го вида - 1 р. прибыли. Каков должен быть план выпуска трансформаторов обоих видов, чтобы цех поучил максимальную прибыль, если и цехе имеется 480 кг железа и 300 кг проволоки.
ТЕМА 2. Решение задачи линейного программирования по оптимизации плана производства с целью получения минимума затрат на ресурсы (на минимум).
Из листового проката определенной формы необходимо вырезать заготовки двух типов А и В. Возможны четыре варианта раскроя одного листа проката. Количество заготовок А и В, вырезаемых из одного листа при каждом варианте раскроя, и отходы раскроя показаны в таблице:
Для изготовления одного изделия нужны 2 заготовки А и 10 заготовок В. Какое количество листов нужно раскроить каждым вариантом раскроя для изготовления 90 штук изделий, чтобы отходы от раскроя были минимальны
ТЕМА 3. Решение задачи распределения ограниченных ресурсов на сетевой модели эвристическими методами с целью минимизации времени выполнения технологического процесса (максимум ресурсов, минимум позднего времени наступления события). Y=5
ТЕМА 4. Прогнозирование производства и товарооборота методом построения линейной модели и определение оптимального объема производства.
ТЕМА 5. Решение задачи оптимизации сложного технологического процесса (задача о покрытии, коммивояжера и определение параметров сетевой модели). Заданы технологические процессы. Определить последовательность исследований, чтобы время было минимально
ОЦЕНКА ВРЕМЕННЫХ ПАРАМЕТРОВ
ОЦЕНКА ФУНКЦИОНИРОВАНИЯ СИСТЕМ
ОЦЕНКА ЭКСПЛУАТАЦИОННОЙ ДОКУМЕНТАЦИИ
ПРОВЕДЕНИЕ РЕГЛАМЕНТА
ТЕМА 6. Решение задачи оптимизации технологических структур (задача о покрытии, коммивояжера на максимум) с целью минимизировать количество действующих элементов.
ОЦЕНКА ВРЕМЕННЫХ ПАРАМЕТРОВ
ОЦЕНКА ФУНКЦИОНИРОВАНИЯ СИСТЕМ
ОЦЕНКА ЭКСПЛУАТАЦИОННОЙ ДОКУМЕНТАЦИИ
ПРОВЕДЕНИЕ РЕГЛАМЕНТА
В скобках стоит продолжительность работы, перед скобкой стоит номер машины на которой происходит обработка изделия.
ТЕМА 8. Решение задачи распределения ресурсов с помощью задачи линейного программирования (задача о назначениях). Даны ракеты и цели, а также вероятности поражения каждой ракетой любой цели. Распределить весь ресурс ракет по воем целям.
Ресурс распределить так, чтобы математическое ожидание числа уничтоженных целей было максимальным. ТЕМА 9 Решение задачи построения организационных структур (задача о покрытии, коммивояжера на минимум и определение параметров загрузки).
ТЕМА 10Решение задачи оптимизации информационных потоков в организационной структуре (по вертикале сверху вниз и обратно).
В.Н. Костин
Пример оформления курсовой работы
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Факультет информационных технологий
Кафедра программного обеспечения вычислительной техники и автоматизированных систем
КУРСОВАЯ РАБОТА по курсу «Оптимизация технологических систем»
Решение задачи линейного программирования по оптимизации плана производства с целью получения максимума прибыли
ГОУ ОГУ 230100.65.6011.10 О
Руководитель работы _____________Костин В.Н. «___»______________2011г. Исполнитель студент гр. 11 ИВТ(м)ИПО _____________Кунафина Н.З. «___»______________2011г.
Оренбург 2011 Содержание Введение………………………………………………………………………………. 3 Постановка задачи……………………………………………………………………. 4 1. Теоретико-методическое описание метода линейного программирования…… 5 2. Области применения и ограничения использования линейного программирования для решения экономических задач………………………………………… 12 3. Оптимизация прибыли с применением метода ЛП……………………………. 16 3.1 Постановка задачи и формирование оптимизационной модели……………... 16 3.2 Расчет и анализ результатов оптимизации прибыли………………………. 16 4 Разработка программы……………………………………………………………. 19 4.1 Инструментальные средства, используемые при разработке………………... 19 4.2 Описание основных процедур и функций……………………………………. 19 Заключение………………………………………………………………………….. 21 Список литературы…………………………………………………………………. 22 Приложение А……………………………………………………………………….. 23
Введение Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, углублением общественного разделения труда, предъявлением высоких требований к методам планирования и хозяйственного руководства. В этих условиях только научный подход к руководству экономической жизнью общества позволит обеспечить высокие темпы развития народного хозяйства. Одним из необходимых условий дальнейшего развития экономической науки является применение точных методов количественного анализа, широкое использование математики. В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение в экономических исследованиях и планировании. Этому способствует развитие таких разделов математики, как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники. Уже накоплен достаточный опыт постановки и решения экономических задач с помощью математических методов. Особенно успешно развиваются методы оптимального планирования, которые и составляют сущность математического программирования. Одной из основных становится задача создания единой системы оптимального планирования и управления народным хозяйством на базе широкого применения математических методов и электронно-вычислительной техники в экономике. Цель курсовой работы: 1. закрепить теоретические знания в области теории методов оптимизации, формирования алгоритмов, написания программ; 2. формирование практических умений в построении алгоритмов и написании программ, реализующих расчетный алгоритм; 3. закрепление практических навыков самостоятельного решения инженерных задач и умений анализировать полученные результаты и делать выводы. Основной целью написания курсовой работы является всесторонний анализ применения линейного программирования для решения задач в сфере электронной коммерции. Задачами курсовой работы являются: 1. Теоретико-методическое описание метода линейного программирования; 2. Выявление области применения и ограничения использования линейного программирования для решения экономических задач в сфере электронной коммерции; 3. Максимизация прибыли посредством использования методов оптимизации для отыскания путей решения данной задачи; 4. Постановка задачи и формирование оптимизационной модели; 5. Расчет и анализ результатов оптимизации прибыли. На современном этапе развития экономики не одна сфера или составная часть производства не может обойтись без оптимизации процессов. Не является здесь исключением и получение максимальной прибыли. Более того, именно получение максимальной прибыли является одной из центральных задач в ведении бизнеса. Базой для выполнения курсового проекта является дисциплина «Оптимизация технологических систем».
Постановка задачи
В ходе курсового проекта необходимо разработать программный продукт, решающий задачи линейного программирования по оптимизации прибыли (на максимум).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.190.88 (0.01 с.) |


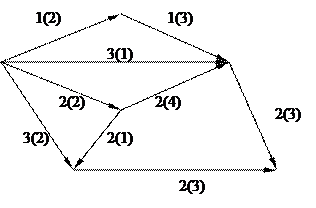
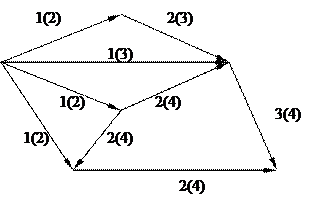 ТЕМА 7.Решение задачи теории расписания на сетевой модели методом ветвей и границ.
ТЕМА 7.Решение задачи теории расписания на сетевой модели методом ветвей и границ.


