
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Понятие линейного программирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§ 1. Понятие математического программирования Формулировка задачи математического программирования Оптимизационные задачи Целевая функция Множество решений Оптимальный план Математическое программирование § 2. История линейного программирования § 3. Задачи экономики, управления и планирования, приводящие к математической задаче линейного программирования Задача об использовании ресурсов (задача планирования производства) Задача составления рациона (задача о диете, задача о смесях) § 4. Общая задача линейного программирования Формулировка задачи линейного программирования в общем виде Каноническая форма задачи линейного программирования
§ 1. Понятие математического программирования
Каждый человек ежедневно, не всегда осознавая это, решает проблему: как получить наибольший эффект, обладая ограниченными средствами. Это может быть личная, семейная задача или производственная необходимость. Чтобы достичь наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий. Можно составить план "на глазок", опираясь на свой опыт и интуицию, но когда дело касается многомиллионного производства, такой метод не годится. В середине XX века был создан специальный математический аппарат, помогающий это делать "по науке". Соответствующий раздел математики называется математическим программированием. Математическая формулировка задачи математического программирования: найти оптимум (максимум или минимум) функции нескольких переменных F (x 1, х 2, …, хп) на множестве X, заданном ограничениями в виде системы уравнений и (или) неравенств. Задача математического программирования относится к оптимизационным задачам, т.е. к задачам на отыскание оптимального значения каких-либо параметров. Функцию F (x 1, х 2, …, хп) называют целевой функцией, или функцией цели, множество X – множеством решений, найденное оптимальное решение Таким образом, математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции нескольких переменных, поэтому, для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Большинство возникающих на практике задач математического программирования слишком громоздки для ручного счета, поэтому их решают с помощью ЭВМ. Все задачи математического программирования делятся на два основных класса: 1) задачи линейного программирования, когда целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств; 2) задачи нелинейного программирования, когда целевая функция или хотя бы одно из ограничений является нелинейной функцией. Линейное программирование – один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого и начала развиваться сама дисциплина "математическое программирование". Термин "программирование" в названии дисциплины ничего общего с термином "программирование (т.е. составление программы) для ЭВМ" не имеет, т.к. дисциплина "линейное программирование" возникла еще до того времени, когда ЭВМ стали широко применяться для решения математических, инженерных, экономических и др. задач. Термин "линейное программирование" возник в результате неточного перевода английского "linear programming". Одно из значений слова "programming" – составление планов, планирование. Следовательно, правильным переводом английского "linear programming" было бы не "линейное программирование", а "линейное планирование", что более точно отражает содержание дисциплины. Однако, термины линейное программирование, нелинейное программирование, математическое программирование и т.д. в нашей литературе стали общепринятыми и поэтому будут сохранены.
§ 2. История линейного программирования Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Леонида Витальевича Канторо́вича "Математические методы организации и планирования производства".
К сожалению, методы, изложенные Л.В.Канторовичем, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, поэтому работа Л.В.Канторовича осталась почти не замеченной.
Примерно в это время Купманс узнал, что еще до войны в далекой России уже было сделано нечто похожее на разработку начал линейного программирования.
В это время Л.В.Канторович продолжает писать математические работы, навеянные экономическими идеями, участвует и в конкретных разработках на производстве. При этом (одновременно с Данцигом, но не зная его работ) он разрабатывает метод, позже названный симплекс-методом. В 1975 году академик Л.В.Канторович и американский профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за "вклад в разработку теории оптимального использования ресурсов в экономике". Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности.
§ 3. Задачи экономики, управления и планирования, приводящие к математической задаче линейного программирования
Линейное программирование применяется при решении некоторых экономических задач; в задачах по управлению и планированию производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д. Приведем пример самых распространенных типов задач. Задача об использовании ресурсов (задача планирования производства). Для изготовления двух видов продукции Р 1 и Р 2 используют четыре вида ресурсов S 1, S 2, S 3 и S 4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (Таблица 1). Таблица 1
Прибыль, получаемая от реализации единицы продукции Р 1 и Р 2, составляет 2 и 3 условных рубля соответственно. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Рассмотрим процесс приведения этой экономической задачи к математическому виду, т.е. составим экономико-математическую модель задачи. Обозначим через х 1 и х 2 – число единиц продукции видов Р 1 и Р 2 соответственно, запланированных к производству. Для их изготовления потребуется согласно таблице данных:
Т.к. потребление ресурсов не должно превышать их запасов, составляющих соответственной 18, 16, 5 и 21 единицу, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
По смыслу задачи переменные х 1 и х 2 неотрицательны, т.е.
Суммарная прибыль F составит: 2 х 1 рублей – от реализации продукции Р 1 и 3 х 2 рублей – от реализации продукции Р 2, т.е.
Итак, экономико-математическая модель задачи: найти такое решение системы неравенств (при условии неотрицательности переменных), при котором функция прибыли принимает максимальное значение. При записи решения это оформляется кратко:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1038; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.241 (0.012 с.) |

 – оптимальным планом.
– оптимальным планом. Леонид Канторович в 1926 году в возрасте четырнадцати лет поступил в Ленинградский университет. Окончил математический факультет (1930), учился в аспирантуре университета, c 1932 года преподаватель, в 1934 стал профессором, в 1935 году ему присвоена учёная степень доктора физико-математических наук без защиты диссертации.
Леонид Канторович в 1926 году в возрасте четырнадцати лет поступил в Ленинградский университет. Окончил математический факультет (1930), учился в аспирантуре университета, c 1932 года преподаватель, в 1934 стал профессором, в 1935 году ему присвоена учёная степень доктора физико-математических наук без защиты диссертации.
 В 1939 году К Канторовичу, 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым нужно было решить задачу о наиболее выгодном распределении материала между станками. Эта задача сводилась к нахождению максимума линейной функции, заданной на многограннике. Максимум такой функции достигался в вершине, однако число вершин в этой задаче достигало миллиарда (!), поэтому простой перебор вершин не годился. Леонид Витальевич писал: "оказалось, что эта задача не является случайной. Я обнаружил большое число разнообразных по содержанию задач, имеющих аналогичный математический характер: наилучшее использование посевных площадей, выбор загрузки оборудования, рациональный раскрой материала, распределение транспортных грузопотоков… Это настойчиво побудило меня к поиску эффективного метода их решения". И уже летом 1939 года была сдана в набор книга Л.В.Канторовича "Математические методы организации и планирования производства", в которой закладывались основания того, что ныне называется математической экономикой.
В 1939 году К Канторовичу, 26-летнему профессору-математику, обратились за консультацией сотрудники лаборатории планерного треста, которым нужно было решить задачу о наиболее выгодном распределении материала между станками. Эта задача сводилась к нахождению максимума линейной функции, заданной на многограннике. Максимум такой функции достигался в вершине, однако число вершин в этой задаче достигало миллиарда (!), поэтому простой перебор вершин не годился. Леонид Витальевич писал: "оказалось, что эта задача не является случайной. Я обнаружил большое число разнообразных по содержанию задач, имеющих аналогичный математический характер: наилучшее использование посевных площадей, выбор загрузки оборудования, рациональный раскрой материала, распределение транспортных грузопотоков… Это настойчиво побудило меня к поиску эффективного метода их решения". И уже летом 1939 года была сдана в набор книга Л.В.Канторовича "Математические методы организации и планирования производства", в которой закладывались основания того, что ныне называется математической экономикой. Концепции Леонида Витальевича вскоре после войны были переоткрыты на западе. Американский экономист Т.Купманс в течение многих лет привлекал внимание математиков к ряду задач, связанных с военной тематикой. Он активно способствовал тому, чтобы был организован математический коллектив для разработки этих проблем.
Концепции Леонида Витальевича вскоре после войны были переоткрыты на западе. Американский экономист Т.Купманс в течение многих лет привлекал внимание математиков к ряду задач, связанных с военной тематикой. Он активно способствовал тому, чтобы был организован математический коллектив для разработки этих проблем. В итоге было осознано, что надо научиться решать задачи о нахождении экстремумов линейных функций на многогранниках, задаваемых линейными неравенствами. По предложению Купманса этот раздел математики получил название линейного программирования.
В итоге было осознано, что надо научиться решать задачи о нахождении экстремумов линейных функций на многогранниках, задаваемых линейными неравенствами. По предложению Купманса этот раздел математики получил название линейного программирования. Американский математик Данциг[13] в 1947 году разработал весьма эффективный конкретный метод численного решения задач линейного программирования (он получил название симплек- метода). Идеи линейного программирования в течение пяти-шести лет получили грандиозное распространение в мире, и имена Купманса и Данцига стали повсюду широко известны.
Американский математик Данциг[13] в 1947 году разработал весьма эффективный конкретный метод численного решения задач линейного программирования (он получил название симплек- метода). Идеи линейного программирования в течение пяти-шести лет получили грандиозное распространение в мире, и имена Купманса и Данцига стали повсюду широко известны. Как легко было бы Данцигу и Купмансу проигнорировать эту информацию! Маленькая книжица, изданная ничтожным тиражом, обращенная даже не к экономистам, а к организаторам производства, с минимумом математики, без четко описанных алгоритмов, без доказательств теорем – словом, стоит ли принимать такую книжку во внимание… Но Купманс настаивает на переводе и издании на западе книги Канторовича. Его имя и идеи становятся известны всем. Воздадим должное благородству американского ученого!
Как легко было бы Данцигу и Купмансу проигнорировать эту информацию! Маленькая книжица, изданная ничтожным тиражом, обращенная даже не к экономистам, а к организаторам производства, с минимумом математики, без четко описанных алгоритмов, без доказательств теорем – словом, стоит ли принимать такую книжку во внимание… Но Купманс настаивает на переводе и издании на западе книги Канторовича. Его имя и идеи становятся известны всем. Воздадим должное благородству американского ученого!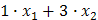 единиц ресурса S 1;
единиц ресурса S 1; единиц ресурса S 2;
единиц ресурса S 2; единиц ресурса S 3;
единиц ресурса S 3; единиц ресурса S 4.
единиц ресурса S 4.
 .
. .
. при ограничениях
при ограничениях


