
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение: Линейное программирование – это раздел математического, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы делятся на универсальные и специальные. С помощью универсальных методов могут быть решены любые задачи линейного программирования. Специальные же методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функций во внутренней точке области допустимых значений. Отсюда – необходимость разработки новых методов. Математическая модель ЗЛП:
при
Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов
Пусть некоторая производственная единица (цех, завод, объединение и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексами j
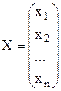
Обозначим через Х=
Так как
Это выражение – целевая функция, которую нужно максимизировать. Так как
Чтобы искомый план Х=
Таким образом, модель задачи о наилучшем использовании ресурсов имеет вид: Найти:
при ограничениях
Т.к. переменные
Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий
В задаче о наилучшем использовании ресурсов определяется оптимальный план выпуска продукции. Пусть при производстве какого-то общественно необходимого продукта используется n технологий. При этом требуется m видов ресурсов, заданных объемами
при ограничениях на лимитируемые ресурсы
и условия неотрицательности
Примеры экономических задач линейного программирования. Задача о смесях
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходным материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе относят задачи о выборе диеты, составления кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности и т.д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы. Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете. Имеются пищевые продукты, известные под номерами 1, 2, 3,..., j,..., n. Они содержат различные питательные вещества, обозначаемые номерами 1, 2, 3,..., i,..., m (углеводы, белки, жиры, витамины, микроэлементы и др.). Единица j-го продукта содержит Математическая модель задачи: Найти:
при ограничениях
Примеры экономических задач линейного программирования. Транспортная задача
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям, при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем, потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. От схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны. Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено
Известны величины
Матрица Х=||
С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи:
Математическая модель транспортной задачи: целевая функция, описывающая транспортные затраты,
минимизируется при ограничениях на возможности поставщиков: весь продукт из пункта производства должен быть вывезен:
на спрос потребителей, который должен быть удовлетворен:
при условии неотрицательности переменных, исключающем обратные перевозки
Определение: Общей задачей линейного программирования называют задачу:
при ограничениях
где Определение: Симметричной формой записи задачи линейного программирования называют задачу:
при ограничениях
или задачу при ограничениях
Определение: Канонической формой записи задачи линейного программирования называют задачу:
при ограничениях
Рассмотрим еще два вида записи- матричную и векторную. Введем обозначения:
где С – матрица-строка; А – матрица системы уравнений, Х – матрица-столбец переменных, Каноническая форма записи примет вид:
или max Z=CX при ограничениях
или
Запишем задачу линейного программирования в векторной форме:
Тогда задача линейного программирования в канонической форме записи имеет вид:
при ограничениях
где
1.10. Способы преобразования
При необходимости задачу минимизации можно заменить задачей максимизации и наоборот. Для функции одной переменной это утверждение очевидно. В самом деле, если Итак, min f(
Рис. 1. Графики функций y=f(x) и y=-f(x). То же самое имеет место в случае функции n переменных:
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.118.154 (0.012 с.) |



 . Предприятие при производстве этих видов продукции должно ограничиваться имеющими видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Пусть их число равно m, припишем им индекс i
. Предприятие при производстве этих видов продукции должно ограничиваться имеющими видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Пусть их число равно m, припишем им индекс i  . Они ограничены, и их количества равны соответственно
. Они ограничены, и их количества равны соответственно  условных единиц. Таким образом,
условных единиц. Таким образом,  - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчислимая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д.
- вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчислимая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д. Примем в качестве такой меры, например, цену реализации
Примем в качестве такой меры, например, цену реализации  (
( ), т.е.
), т.е.  - вектор цен. Известны также технологические коэффициенты
- вектор цен. Известны также технологические коэффициенты  , которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов ||
, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов ||  .
. - план производства, показывающий какие виды товаров нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
- план производства, показывающий какие виды товаров нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.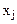 единиц будет равна
единиц будет равна  , а общий объем реализации:
, а общий объем реализации: .
. - расход i-го ресурса на производство
- расход i-го ресурса на производство  (
( ) единиц:
) единиц:
 , (
, ( ,
, (
( ),
), ,
, (
( (
( (
( .
. - затраты на перевозку единицы продукта из i-го пункта производства в j-тый пункт потребления. Обозначим через
- затраты на перевозку единицы продукта из i-го пункта производства в j-тый пункт потребления. Обозначим через  количество продукта, перевозимое из i-го пункта производства в j-тый пункт потребления. Матрица С=||
количество продукта, перевозимое из i-го пункта производства в j-тый пункт потребления. Матрица С=|| 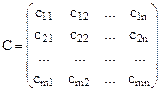

























 ,
, (
( (
(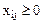 (
(
 1.9. Основные виды записи задач линейного программирования
1.9. Основные виды записи задач линейного программирования
 );
); (
( );
); (
( );
);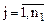 );
); ),
),
 ,
, ,
,  ,
, - матрица-столбец свободных членов.
- матрица-столбец свободных членов.
 ,
, 
 ,
,  ,
,  ,...,
,...,  ,...,
,...,  .
.
 ,
, 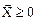 ,
, - скалярное произведение векторов
- скалярное произведение векторов  .
. - точка максимума функции y=f(x), то для функции y=-f(x) она является точкой максимума, так как графики функций f(x) и –f(x) симметричны относительно оси абсцисс (рис. 1).
- точка максимума функции y=f(x), то для функции y=-f(x) она является точкой максимума, так как графики функций f(x) и –f(x) симметричны относительно оси абсцисс (рис. 1).
 .
.


