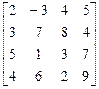Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричные игры с нулевой суммойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория игр занимается разработкой различного рода рекомендаций по принятию решений в условиях конфликтной ситуации. Формализуя конфликтные ситуации, их можно представить как игру двух, трех и более игроков, каждый из которых преследует цель максимизации прибыли за счет других игроков. Определение 1: Теория игр – это раздел математики, занимающийся выработкой оптимальных правил поведения для каждой стороны, участвующей в конфликтной ситуации. Определение 2: Совокупность правил, однозначно определяющих последовательность действий стороны в конкретной конфликтной ситуации, есть стратегия. Определение 3: Под игрой понимается совокупность предварительно оговоренных правил и условий. Определение 4: Частичная возможная реализация правил игры называется партия. Если n партнеров (игроков) участвуют в данной игре, то основной вопрос теории игр заключается в следующем: как должен вести себя j-ый партнер для достижения наиболее благоприятного для себя исхода? В конце партии каждый игрок получает сумму В большинстве случаев мы будем иметь дело с играми с нулевой суммой, т.е. Определение 5: Игры, в которых участвуют два игрока, называются парными, а с большим числом игроков – множественными. Определение 6: Принятие игроком того или иного решения в процессе игры и его реализация называется ходом. Ходы могут быть личные (ход выбран сознательно) и случайные (ход выбран на основании метода случайного выбора). В зависимости от количества стратегий игры делятся на конечные и бесконечные. В конечной игре каждый игрок имеет конечное число стратегий, в бесконечной – бесконечное. В зависимости от взаимоотношений игроков игры делятся на кооперативные, коалиционные и бескоалиционные. Если игроки не имеют право вступать ни в какие соглашения, то игра будет бескоалиционная. Если же они имеют право вступать в коалиции – коалиционные. Кооперативная игра – это игра, в которой заранее определены все коалиции. В зависимости от функции выигрыша игры делятся на матричные, непрерывные, выпуклые и т.д. Мы будем рассматривать матричные игры. Пример 1: Игра "орел – решка". Играют два игрока. Каждый игрок выбирает одну из сторон монеты: орел или решку. По очереди они бросают монету. Выигрывает тот, кто угадал выпавшую сторону монеты. Пример 2: Игра "в три пальца". Играют два игрока. Оба игрока одновременно и независимо друг от друга показывают один, два или три пальца. Если общее количество пальцев число четное, то эту сумму выигрывает первый игрок, если нечетное, то ее выигрывает второй игрок. В общем случае матричная игра задается прямоугольной матрицей размером m
Каждый элемент Матричную игру часто записывают в развернутой форме в виде таблицы, которую называют платежной матрицей:
Каждый игрок выбирает для себя наиболее выгодную стратегию. При этом первый игрок стремится выигрыш максимизировать, а второй – минимизировать проигрыш. В связи с этим вводятся понятия нижней и верхней цены игры. Определение 7: Нижней чистой ценой игры (максимином) называется число α, определяемое по формуле:
Определение 8: Верхней чистой ценой игры (минимаксом) называется число β, определяемое по формуле:
Определение 9: Стратегии игроков, соответствующие максимину (минимаксу), называются максиминными (минимаксными). Пример 3: Найти максиминную и минимаксную стратегии игроков в матричной игре:
Решение.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 768; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 (
(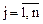 ), которую будем называть выигрышем. При этом подразумевается, что каждый игрок пытается свой выигрыш максимизировать. Числа
), которую будем называть выигрышем. При этом подразумевается, что каждый игрок пытается свой выигрыш максимизировать. Числа  . В этих играх сумма выигрыша переходит от одного игрока к другому, не поступая из дополнительных источников.
. В этих играх сумма выигрыша переходит от одного игрока к другому, не поступая из дополнительных источников. n. Номер i-ой строки соответствует номеру стратегии
n. Номер i-ой строки соответствует номеру стратегии  , применяемой первым игроком. Номер j-ого столбца соответствует стратегии
, применяемой первым игроком. Номер j-ого столбца соответствует стратегии 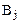 , применяемой вторым игроком. Описанная игра однозначно определяется матрицей:
, применяемой вторым игроком. Описанная игра однозначно определяется матрицей: .
. матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую вторым игроком первому, если первый игрок выбирает строку, соответствующую i-той строке, а второй игрок – j-тому столбцу.
матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую вторым игроком первому, если первый игрок выбирает строку, соответствующую i-той строке, а второй игрок – j-тому столбцу.







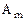



 .
.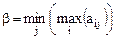 .
.