
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матричный метод анализа сетей Петри.Содержание книги
Поиск на нашем сайте
Сети Петри - это математическая модель, которая имеет широкое применение для описания поведения параллельных устройств и процессов. Сеть Петри есть двудольный ориентированный граф. Двудольный граф - это такой граф, множество вершин которого разбивается на два подмножества и не существует дуги, соединяющей две вершины из одного подмножества. Итак, сеть Петри - это набор N = (T,P,A), T Ç Р = Ø, где Т = {t1, t2,..., tn} - подмножество вершин, называющихся переходами; По определению, дуга соединяет либо место с переходом, либо переход с местом. Данный подход основан на матричном представлении сетей Петри. Входная и выходная функции представляются матрицами
Матричная форма представления сети C = <P (множество позиций), T (множество переходов), Пусть е [ j ] – m -вектор - столбец, содержащий все нули, за исключением j -й позиции. Переход Переход σ (μ, где ( Тогда для последовательности запусков переходов σ = δ (μ, σ) = μ + De [ ,где ƒ(σ) = ﴾ e [ Для того чтобы показать сохранение сети, необходимо найти (ненулевой) вектор взвешивания ω, размерностью (1 × n), для которого взвешенная сумма по всем маркировкам постоянна, т.е. ωμ = ωμ'. Поскольку маркировка μ' достижима, существует последовательность запусков переходов σ, которая переводит сеть из μ в μ': μ' = μ + Df (σ). Следовательно, ωμ = ωμ' = ω ﴾ μ + Df (σ)﴿= ωμ + ωDf (σ). Отсюда следует, что ωDf (σ) = 0. Поскольку это должно быть справедливо для всех f (σ), то ωD = 0. Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой вектор ω, что ωD = 0. Если ω = (1, 1,..., 1), то это условие формулируется следующим образом: сумма элементов каждого столбца матрицы D должна быть нулевой. Матричная теория сетей Петри является инструментом для решения проблемы достижимости. Предположим, что маркировка μ' достижима из маркировки μ. Тогда существует последовательность запусков переходов σ, которая приводит из μ к μ'. Это означает, что f (σ) является неотрицательным целым решением следующего матричного уравнения для х: μ' = μ+Dx. (2.1) Если μ' достижима из μ, тогда уравнение имеет решение в неотрицательных целых, если уравнение не имеет решения, то μ' недостижима из μ. Наличие решения уравнения (2.1) является необходимым, но не достаточным для достижимости. Необходимо проверить, существует ли разрешенная последовательность запуска переходов, соответствующая вектору разметки μ'. Пример: Рассмотрим сеть, представленную на рис. 1.
Рис. 1. Пример для иллюстрации матричного представления сетей Петри Матрицы
В начальной маркировке μ =
Последовательность σ =
Для определения того, является ли маркировка μ' =
Система этих уравнений имеет решение Матричный подход к анализу сетей очень перспективен, но имеет и ряд недостатков. Матрица D сама по себе не полностью отражает структуру сети, так как встречные дуги между переходом и позицией (как, например, между В качестве положительных свойств матричного метода анализа следует отметить компактность представления информации и высокую степень формализации, облегчающую применение средств вычислительной техники.
12. Дерево достижимости и его свойства, алгоритм построения дерева, теорема оконечности дерева достижимости (без доказательства). Анализ сетей Петри с использованием дерева достижимости.
Дерево достижимости – это исходящее дерево, вершинам которого соответствуют достижимые маркировки сети Петри. Начальной маркировке соответствует корневая вершина. Если из вершины μ' в вершину μ" ведет дуга, то она взвешена переходом, переводящим сеть Петри из маркировки μ' в μ".
Всякий путь от корня в дереве соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера, т.е. найти средства, которые ограничивают введение новых маркировок на каждом шаге построения. В этом смысле выделяют пассивные (терминальные), дублирующие вершины и вершины с расширенной маркировкой. Пассивная (или терминальная) вершина – это маркировка, в которой нет разрешенных переходов ((0, 0, 1) для рис. 1). Дублирующая вершина – это вершина с маркировкой, которая уже ранее встречалась в этом дереве достижимости. При появлении дублирующей вершины нет необходимости производить из нее дальнейшие построения, поскольку это приведет к появлению поддерева, полученного из места первого появления дублирующей вершины. В рассматриваемом примере маркировка (0, 1, 1), получившаяся после выполнения t1, t2, t3 не будет порождать какие-либо новые вершины, поскольку она ранее была получена в дереве после выполнения t2 из начальной маркировки. Расширенная маркировка вводится в случае постепенного наращивания количества фишек в той или иной позиции достигаемых маркировок. Для рассматриваемого примера (см. рис. 1) последовательное срабатывание t1 приводит к нарастанию разметки в позиции р2, что приводит к введению расширенной маркировки (1, ω, 0). Кроме того, различают граничные вершины и внутренние. Граничными вершинами называют вершины дерева достижимости, которые еще не обработаны алгоритмом построения дерева достижимости. В результате реализации алгоритма построения дерева достижимости граничные вершины превращаются в терминальные, дублирующие или внутренние. Алгоритм построения (конечного) дерева Пусть x - граничная вершина, которую нужно обработать. 1) если в дереве есть другая вершина Такая обработка алгоритмом граничных вершин продолжается до тех пор, пока все вершины дерева не станут терминальными, дублирующими или внутренними. Затем алгоритм останавливается. Теорема о конечности дерева достижимости (без доказательства) Существующий алгоритм построения ограниченного дерева достижимости применим для любой возможной сети Петри. Или Для любой сети Петри можно с помощью приведенного алгоритма построить ограниченное дерево достижимости.
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 и
и 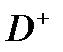 соответственно. Элементы матриц определяются следующим образом:
соответственно. Элементы матриц определяются следующим образом: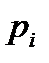 , I (
, I (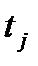 )); (количество фишек уходящее из позиции
)); (количество фишек уходящее из позиции  ; j=
; j=  .
.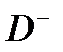 ,
, 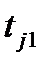 ,
, 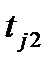 ,...,
,...,  имеем
имеем ] + De [
] + De [ 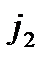 ] +... + De [
] +... + De [ 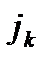 ] = μ + D ﴾ e [
] = μ + D ﴾ e [ 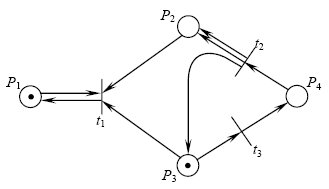
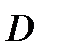 для этой сети имеют следующий вид:
для этой сети имеют следующий вид: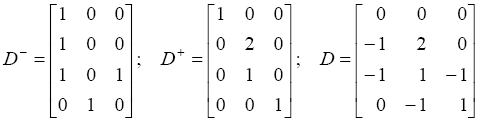
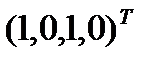 переход
переход 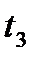 разрешен и приводит к маркировке:
разрешен и приводит к маркировке: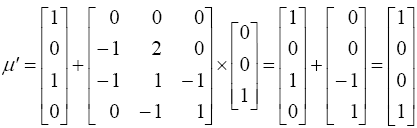
 ,
, 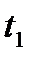 представляется вектором запусков f (σ) =
представляется вектором запусков f (σ) = 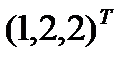 и приводит к маркировке
и приводит к маркировке
 достижимой из маркировки μ = (1, 0, 1, 0), имеем линейные уравнения
достижимой из маркировки μ = (1, 0, 1, 0), имеем линейные уравнения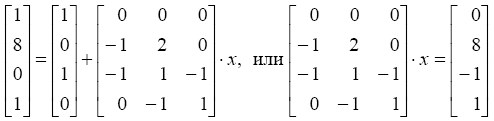
 = (0,4,5). Это соответствует разрешенной последовательности σ =
= (0,4,5). Это соответствует разрешенной последовательности σ =  и
и  , то х – дублирующая.
, то х – дублирующая. 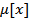 ни один из переходов неразрешён, т.е.
ни один из переходов неразрешён, т.е.  не определено для
не определено для 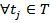 , то х – терминальная вершина.
, то х – терминальная вершина. 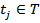 разрешённого в
разрешённого в 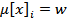 , то
, то  .
. 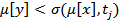 и
и  , то
, то  .
.


