
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ сетей Петри с использованием дерева достижимости.Содержание книги
Поиск на нашем сайте
Анализ ограниченности: Сеть Петри ограничена тогда и только тогда, когда символ ω отсутствует в дереве достижимости. Если символа ω нет, то можно определить границу числа меток в позициях путем перебора вершин дерева достижимости. Анализ сохранения: Если эта сумма фишек одинакова для каждой достижимой маркировки, то сеть Петри является сохраняющей. Если суммы не равны, сеть не является сохраняющей. Если маркировка некоторой позиции совпадает с , то эта позиция должна был исключена из рассмотрения. Анализ покрываемости: Проверяемая разметка покрываема, если она является вершиной дерева достижимости. Анализ живости: изучение возможности срабатывания перехода. Переход сети Петри называют тупиковым, если в процессе функционирования сеть может оказаться в состоянии, в котором этот переход заблокирован. Нетупиковый переход называют активным. • активность уровня 0, если он никогда не может быть активирован (пассивный или «мёртвый» переход); • активность уровня 1, если существует состояние (достижимое из начального), в котором он активирован;(«потенциально живой» переход) • активность уровня 2, если для всякого целого n существует последовательность срабатывания переходов, в которой данный переход присутствует по крайней мере n раз; • активность уровня 3, если существует бесконечная последовательность срабатывания переходов, в которой данный переход присутствует неограниченно часто; • активность уровня 4, если для любого достижимого состояния существует последовательность срабатываний, приводящая в такое состояние, в котором этот переход активирован (активный или «живой» переход).
Реляционная алгебра. Отношения, кортежи, атрибуты, домены.
Реляционная алгебра — формальная система манипулирования отношениями в реляционной модели данных. Основная идея реляционной алгебры состоит в том, что коль скоро отношения являются множествами, средства манипулирования отношениями могут базироваться на традиционных теоретико-множественных операциях, дополненных некоторыми специальными операциями, специфичными для реляционных баз данных. Существует много подходов к определению реляционной алгебры, которые различаются наборами операций и способами их интерпретации, но, в принципе, являются более или менее равносильными. В данном случае мы рассматриваем алгебру Кодда. В этом варианте набор основных алгебраических операций состоит из восьми операций, которые делятся на два класса – теоретико-множественные операции и специальные реляционные операции. Отношение — фундаментальное понятие реляционной модели данных. По этой причине модель и называется реляционной. N-арным отношением R называют подмножество декартового произведения множеств (Другое определение: Отношением называется некоторое подмножество декартового произведения одного или нескольких доменов) Под доменом будем понимать некоторое множество значений. Домен - множество значений данных какого-либо типа. Каждый атрибут может быть определен на каком-либо одном домене. На одном домене может быть определено несколько атрибутов. Отношение имеет простую графическую интерпретацию, оно может быть представлено в виде таблицы, столбцы которой соответствуют вхождениям доменов в отношение, а строки - наборам из n значений, взятых из исходных доменов.
Реляционная алгебра. Операции реляционной алгебры.
Реляционная алгебра — это система манипулирования отношениями, которые являются элементами, группируемыми во множество. Реляционная алгебра — формальная система манипулирования отношениями в реляционной модели данных. Основные восемь операций реляционной алгебры были предложены Э.Коддом. · Объединение · Пересечение · Вычитание · Декартово произведение · Выборка · Проекция · Соединение · Деление Проекция
Выборка
Умножение
Соединение и естественное соединение
Пересечение и вычитание.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.195 (0.008 с.) |

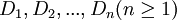 , не обязательно различных. Исходные множества D1,D2,...,Dn называют в модели доменами.
, не обязательно различных. Исходные множества D1,D2,...,Dn называют в модели доменами.


