
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие существования префиксного кода, неравенство и теорема Крафта.Содержание книги
Поиск на нашем сайте
Префиксным кодом называется алфавитный код, в котором ни одно из кодовых слов не является префиксом никакого другого кодового слова. Любой префиксный код является разделимым. В теории кодирования, неравенство Крафта — Макмиллана даёт необходимое и достаточное условие существования разделимых и префиксных кодов, обладающих заданным набором длин кодовых слов.
Теорема (необходимые условия). Пусть
Доказательство. Рассмотрим, сколько слов длины Для каждого кодового слова длины
Это неравенство верно для любого
Слагаемое вида
С учетом такого представления неравенство (6.5) можно переписать следующим образом:
где Выполнение неравенства Крафта доказано для префиксного кода. Однако в 1956 году Мак-Милан доказал более общую теорему, согласно которой неравенство Крафта выполняется и для любого однозначно декодируемого кода. Доказательство теоремы изложено в[29], [31]. Можно также доказать, что если префиксный код полный, то в нестрогом неравенстве (6.3) будет выполняться равенство. Теорема (достаточные условия). Если положительные целые числа
то существует префиксный код Доказательство. Если среди чисел
где Для построения нужного префиксного кода должна быть возможность подходящим образом выбрать Из неравенства (6.4) при
Аналогично, при
Правая часть его вновь совпадает с допустимым для построения префиксного кода числом вершин третьего яруса, если на первых двух ярусах уже выбраны Докажем, что если для длин Теоремы Крафта доказаны для случая, когда рассматриваются коды в алфавите
Оказывается, этому неравенству обязаны удовлетворять и длины кодовых слов произвольного однозначно декодируемого кода. Поэтому, если существует однозначно декодируемый код с длинами слов
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 947; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.110.231 (0.006 с.) |

 - префиксный двоичный код с длинами кодовых слов
- префиксный двоичный код с длинами кодовых слов  . Тогда выполняется неравенство Крафта
. Тогда выполняется неравенство Крафта
 может быть в префиксном коде. Максимальное число таких слов равно
может быть в префиксном коде. Максимальное число таких слов равно  . В этом случае все
. В этом случае все  имеется
имеется  слов длины
слов длины  и
и  слов длины
слов длины  и
и  являются префиксами, не пересекаются, так как в противном случае более короткое из этих слов было бы префиксом более длинного. Значит, если в префиксном коде имеется
являются префиксами, не пересекаются, так как в противном случае более короткое из этих слов было бы префиксом более длинного. Значит, если в префиксном коде имеется  слов длины
слов длины  слов длины
слов длины  слов длины 1, то число
слов длины 1, то число  слов длины
слов длины 
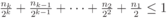
 , представляющее в неравенстве (6.5)
, представляющее в неравенстве (6.5)  кодовых слов длины
кодовых слов длины  , можно записать в виде суммы
, можно записать в виде суммы

 - общее число слов префиксного кода. Теорема доказана.
- общее число слов префиксного кода. Теорема доказана.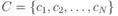 с длинами кодовых слов
с длинами кодовых слов 
 имеется ровно
имеется ровно  чисел, равных
чисел, равных  , то неравенство Крафта можно записать в виде
, то неравенство Крафта можно записать в виде
 - максимальное из данных чисел. Из справедливости этого неравенства следует, что верны неравенства (6.5) для всех
- максимальное из данных чисел. Из справедливости этого неравенства следует, что верны неравенства (6.5) для всех  , а следовательно, и неравенство (6.4).
, а следовательно, и неравенство (6.4). слов длины 1,
слов длины 1,  слов длины 2, вообще
слов длины 2, вообще  или, иными словами,
или, иными словами,  - на
- на  получаем
получаем  , т. е. требуемое число не превосходит общего числа вершин первого яруса. Значит, на этом ярусе можно выбрать какие-то
, т. е. требуемое число не превосходит общего числа вершин первого яруса. Значит, на этом ярусе можно выбрать какие-то  ) для построения кода можно использовать лишь
) для построения кода можно использовать лишь  . Однако и этого числа вершин хватит, так как из неравенства (6.4) при
. Однако и этого числа вершин хватит, так как из неравенства (6.4) при  вытекает
вытекает
 имеем неравенство:
имеем неравенство:
 кодовых вершин на третьем ярусе. Продолжая этот процесс вплоть до
кодовых вершин на третьем ярусе. Продолжая этот процесс вплоть до  , мы и получим требуемый код. Теорема доказана.
, мы и получим требуемый код. Теорема доказана. ,то код является полным. Предположим противное, то есть, что код не полный. Тогда к нему можно добавить, по крайней мере, одно кодовое слово (длины
,то код является полным. Предположим противное, то есть, что код не полный. Тогда к нему можно добавить, по крайней мере, одно кодовое слово (длины 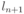 ) и получить новый префиксный код, для которого, с одной стороны,
) и получить новый префиксный код, для которого, с одной стороны, 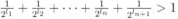 , а с другой стороны, в силу теоремы Крафта,
, а с другой стороны, в силу теоремы Крафта,  Полученное противоречие доказывает утверждение.
Полученное противоречие доказывает утверждение.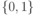 . Если кодовый алфавит содержит
. Если кодовый алфавит содержит  символов, то аналогичным образом можно доказать, что необходимым и достаточным условием для существования префиксного кода с длинами слов
символов, то аналогичным образом можно доказать, что необходимым и достаточным условием для существования префиксного кода с длинами слов 



