
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели операцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для применения количественных методов исследования в любой области всегда требуется какая-то математическая модель. При построении модели реальное явление (в нашем случае – операция) неизбежно упрощается, схематизируется, и эта схема описывается с помощью того или иного математического аппарата. Общих способов построения математических моделей не существует. В каждом конкретном случае модель выбирается исходя из вида операции, ее целевой направленности, с учетом задачи исследования (какие параметры требуется определить и влияние каких факторов отразить). Необходимо также в каждом конкретном случае соразмерять точность и подробность модели: а) с той точностью, с которой нужно знать решение; б) с той информацией, которой мы располагаем или можем приобрести. Если исходные данные, нужные для расчетов, известны неточно, то, очевидно, нет смысла входить в тонкости, строить очень подробную модель и тратить время (свое и машинное) на тонкую и точную оптимизацию решения. К сожалению, этим принципом часто пренебрегают и выбирают для описания явлений слишком подробные модели. Математическая модель должна отражать важнейшие черты явления, все существенные факторы, от которых зависит успех операции. Вместе с тем модель должна быть по возможности более простой. Две опасности всегда подстерегают составителя модели: первая – увязнуть в подробностях и вторая – слишком огрубить явление. Создание математической модели – самая важная и ответственная часть исследования, требующая глубокого знания не столько математики, сколько существа моделируемых явлений. Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества вариантов в условиях рыночных отношений приходится отыскивать наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические и технологические возможности. До недавнего времени большинство таких задач решалось исходя из здравого смысла и опыта лиц, принимающих решения, или просто «на глаз». При таком подходе не было и не могло быть никакой уверенности, что найденный вариант – наилучший. При современных масштабах производства даже незначительные ошибки оборачивались громадными потерями. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику. Такие методы объединяются под общим названием – математическое программирование.
Определение: Математическое программирование – область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Определение: Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности. Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель. Определение: Математическая модель задачи – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д. Математическая модель задачи математического программирования включает: · совокупность неизвестных величин
действуя на которые систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, стратегией, поведением и др.); · целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбрать наилучший вариант из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение; · условия (или систему ограничений), налагаемые на неизвестные величины. Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Ограниченными являются не только материальные, финансовые и трудовые ресурсы, но и таковыми могут быть возможности технического, технологического и, вообще, научного потенциала. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений (область экономических возможностей). Объединение всех условий (ограничений), налагаемых на известные (искомые) величины
В развернутом виде: найти план max (min) Z = z при ограничениях
Замечание: надпись « Из экономических или физических соображений на план задачи или некоторые его компоненты (координаты) накладываются условия не отрицательности:
иногда – целочисленности. Определение: План Х, удовлетворяющий системе ограничений задачи, называется допустимым (ХÎW). Определение: Допустимый план, доставляющий функции цели экстремальное значение, называется оптимальным. Оптимальный план будем обозначать
|
||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.231.40 (0.01 с.) |

 ,
,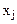 задачи, обозначим: W (хÎW). При таких обозначениях модель задачи математического программирования примет вид: max (min) Z = z(x), xÎW, или найти extremum Z = z(x), xÎW.
задачи, обозначим: W (хÎW). При таких обозначениях модель задачи математического программирования примет вид: max (min) Z = z(x), xÎW, или найти extremum Z = z(x), xÎW.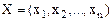 , доставляющий экстремальное значение целевой функции z, т.е.
, доставляющий экстремальное значение целевой функции z, т.е.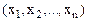
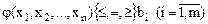
 » означает «i изменяется от 1 до m».
» означает «i изменяется от 1 до m».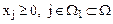 ,
, , экстремальное значение функции цели – z(
, экстремальное значение функции цели – z( . Оптимальное решение, вообще говоря, не обязательно единственное, возможны случаи, когда оно не существует, имеется конечное или бесконечное множество оптимальных решений.
. Оптимальное решение, вообще говоря, не обязательно единственное, возможны случаи, когда оно не существует, имеется конечное или бесконечное множество оптимальных решений.


