
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение транспортных задач с ограничениями по пропускной способностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В некоторых случаях в условии транспортной задачи накладываются дополнительные ограничения на пропускную способность линии связи. Будем их обозначать Решаются такие задачи обычным образом, но с дополнительными особенностями. Алгоритм решения транспортных задач с ограничениями по пропускной способности: 1. Построение начального опорного плана можно осуществлять любым методом (правило северо-западного угла, минимального элемента, метод Фогеля). Лучше всего: по правилу минимального элемента. Особенность построения начального опорного плана заключается в следующем: в выбранную ячейку ставится минимальное из чисел 2. Расчет потенциалов производится по базисным ячейкам. Расчет оценок свободных и дополнительных ячеек производится обычным образом. Однако, для оптимальности опорного плана необходимо, чтобы оценки дополнительных ячеек были неположительны. Для свободных ячеек оценки должны быть неотрицателтьны, а для базисных равны 0. 3. Если полученный опорный план не оптимален, то обычным образом строят цикл. производят перемещение груза по циклу и снова определяют оптимальность полученного решения. Пример: Решить транспортную задачу с ограничениями по пропускной способности:
Базисных переменных: 5+3-1=7. Дополнительная переменная 1. Сосчитаем оценки:
Получились две отрицательные оценки. Строим цикл.
Базисных переменных: 5+3-1=7. Дополнительная переменная 1. Сосчитаем оценки:
Полученный план оптимален. Z=5*10+2*130+1*80+6*70+3*70+4*70+ +2*90+2*0=1480 Ответ: Z=1480.
Примеры задач дискретного программирования. Задача о контейнерных перевозках. Задача о назначении
Дискретное программирование – это раздел математического программирования и изучающий экстримальные задачи, в которых на искомые переменные налагаются условия целочисленности, а область допустимых решений конечна. Дискретное программирование также называется целочисленным. Задача о контейнерных перевозках (о рюкзаке или о бомбардировщике). Контейнер оборудован m отсеками, вместимостью
при
Задача о назначении (проблема выбора, о женихах и невестах). Имеется n исполнителей, которые могут выполнять n различных работ. Известна полезность Для составления математической модели задачи обозначим через
Так как нужно найти план назначения
при а) каждый исполнитель назначается только на одну работу:
б) на каждую работу назначается только один исполнитель:
Мы рассмотрели только два примера, можно еще рассмотреть задачу коммивояжера, транспортную задачу с фиксированными доплатами.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.110 (0.008 с.) |

 . Тогда говорят о разновидности транспортных задач – транспортных задачах с ограничениями по пропускной способности. Все ограничения записываются в левом нижнем углу ячейки. Они означают, что больше чем записано в ячейку загрузить нельзя.
. Тогда говорят о разновидности транспортных задач – транспортных задачах с ограничениями по пропускной способности. Все ограничения записываются в левом нижнем углу ячейки. Они означают, что больше чем записано в ячейку загрузить нельзя. ,
,  и
и 

 БП
БП
 БП
БП
 7
– 0
БП
7
– 0
БП

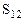 =8-(-2+4)=6>0
=8-(-2+4)=6>0
 =5-(2-1)=4>0
=5-(2-1)=4>0
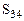 =3-(4+0)=-1<0
=3-(4+0)=-1<0
 =7-(-2+2)=7>0
=7-(-2+2)=7>0
 =4-(4-1)=3>0
=4-(4-1)=3>0
 =2-(3+0)=-1<0
=2-(3+0)=-1<0
 =3-(4-1)=0=0
=3-(4-1)=0=0
 =6-(3-1)=4>0
=6-(3-1)=4>0
 =7-(6+0)=1>0
=7-(6+0)=1>0
 (
(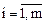 ). Для перевозки n видов продукции. Виды продукции характеризуются свойствами неделимости. Пусть
). Для перевозки n видов продукции. Виды продукции характеризуются свойствами неделимости. Пусть  – расход i-того отсека для перевозки j-той продукции. Обозначим через
– расход i-того отсека для перевозки j-той продукции. Обозначим через  полезность единицы j-й продукции. Требуется найти план перевозки, при котором прибыль от перевозки максимизируется:
полезность единицы j-й продукции. Требуется найти план перевозки, при котором прибыль от перевозки максимизируется:


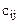 , связанная с выполнением i-м исполнителем j-той работы (i,j=
, связанная с выполнением i-м исполнителем j-той работы (i,j= 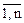 ). Нужно так назначить исполнителей на работы, чтобы добиться максимальной полезности при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой должен быть закреплён только один исполнитель.
). Нужно так назначить исполнителей на работы, чтобы добиться максимальной полезности при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой должен быть закреплён только один исполнитель. – факт назначения или не назначения i-того исполнителя на j-ю работу. Так как количество исполнителей равно количеству работ и каждый из них может быть назначен только на одну работу, то
– факт назначения или не назначения i-того исполнителя на j-ю работу. Так как количество исполнителей равно количеству работ и каждый из них может быть назначен только на одну работу, то 



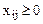 ,
,  - ограничение неотрицательности и целочисленности.
- ограничение неотрицательности и целочисленности.


