
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача выпуклого программированияСодержание книги
Поиск на нашем сайте
Определение 1: Функция f(x), определенная на выпуклом множестве Х, называется выпуклой, если для любых точек
Если в этом соотношении при Определение 2: Функция f(x), определенная на выпуклом множестве Х, называется вогнутой, если для любых точек
Если в этом соотношении при Определение 3: Задача математического программирования
при ограничениях
в которой либо целевая функция, либо ограничения, либо то и другое нелинейны, называется нелинейной. Класс задач нелинейного математического программирования очень велик. Общих универсальных методов нет. Однако, есть задачи нелинейного программирования, для которых есть методы решения. Один из таких типов задач являются задачи выпуклого программирования. В теории выпуклого программирования в качестве основной обычно рассматривается задача минимизации выпуклой функции n переменных Если
Метод множителей Лагранжа
Метод множителей Лагранжа является классическим методом решения задач математического программирования (в частности выпуклого). Рассмотрим классическую задачу оптимизации
при ограничениях
От основной задачи выпуклого программирования в данной постановке задача отличается тем, что в системе ограничений нет неравенств и нет ограничения неотрицательности для переменных. Классический подход к решению данной задачи дает систему уравнений (необходимые условия), которым должна удовлетворять точка Предположим, что в точке
равен m. Тогда необходимые условия запишутся в виде:
где
есть функция Лагранжа, Алгоритм решения задачи методом множителей Лагранжа: 1. Составить функцию Лагранжа. 2. Найти частные производные функции Лагранжа по всем переменным 3. Из стационарных точек, взятых без Пример: Решить задачу математического программирования, используя метод множителей Лагранжа.
при
Решение: Будем решать задачу без учета неотрицательности переменных. 1. Составим функцию Лагранжа.
2. Найдем ее частные производные по
Приравняв производные к нулю, получим систему:
Решим ее:
Получена стационарная точка (91, 89). С помощью вторых производных легко доказать, что в полученной точке функция достигает условный локальный экстремум. Данная точка является точкой минимума функции. Ответ: Z=17278.
Градиентные методы
Градиентным методом можно решать любую нелинейную задачу. При этом находится локальный экстремум. Целесообразнее же этот метод используют при решении задач выпуклого программирования. Будем рассматривать задачу максимизации нелинейной дифференцируемой функции Возьмем произвольную точку Поисковая траектория представляет собой ломаную Градиентные методы, как правило, позволяют найти точные решения за бесконечное число шагов и лишь в некоторых случаях за конечное. В связи с этим градиентные методы относят к приближенным методам решения.
Блок 4
|
||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 1322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.104 (0.006 с.) |

 и
и  из этого множества и любого
из этого множества и любого  справедливо неравенство:
справедливо неравенство: .
.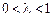 и любых
и любых  Х (
Х ( .
.
 (
(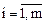 ),
),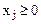 (
(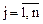 ).
). при ограничениях
при ограничениях 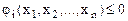 (
(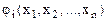 предполагаются выпуклыми.
предполагаются выпуклыми. (
(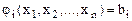 (
(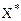 , доставляющая функции
, доставляющая функции 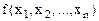 локальный экстремум на множестве точек, удовлетворяющих системе ограничений (для задачи выпуклого программирования найденная точка будет и глобальным экстремум).
локальный экстремум на множестве точек, удовлетворяющих системе ограничений (для задачи выпуклого программирования найденная точка будет и глобальным экстремум).
 (
( (
(
 – множители Лагранжа.
– множители Лагранжа.

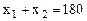 ,
,

 .
.

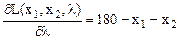





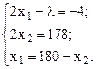



 . Суть градиентного поиска точки максимума:
. Суть градиентного поиска точки максимума: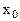 из области допустимых значений. C помощью градиента функции
из области допустимых значений. C помощью градиента функции  Определим направление, в котором
Определим направление, в котором  . Далее снова определяем наилучшее направление для перехода в очередную точку
. Далее снова определяем наилучшее направление для перехода в очередную точку 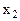 и т.д.
и т.д. . Таким образом, надо построить последовательность
. Таким образом, надо построить последовательность 




