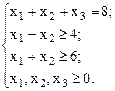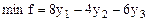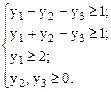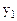Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несимметричные двойственные задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пуст ЗЛП задана в каноническом виде:
при
Переведем данную задачу в симметричную форму:
Прямая задача на максимум, значит неравенства должны быть ≤. Умножим второе неравенство на (-1). Получим:
Составим двойственную задачу для полученной симметричной. Для этого введем двойственные переменные
при ограничениях:
Преобразуем систему ограничений следующим образом:
Обозначим y разность В результате получим двойственную задачу вида:
при
Подводя итоги вышеизложенному, опишем прямую и двойственную задачу для ЗЛП в общем случае:
Таким образом, двойственная задача со смешанными ограничениями составляется с соблюдением следующих дополнительных правил: 1. Если на переменную 2. Если на переменную 3. Если в прямой задачи имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагается условие неотрицительности. Задача двойственная двойственной будет совпадать с исходной. Поэтому безразлично которую задачу можно принять за прямую, которую за двойственную. Следует говорить о паре взаимно двойственных задач. Рассмотри пару двойственных задач. Теорема 1: (об основном неравенстве двойственности) Для любых допустимых планов X=
Экономическое содержание основного неравенства двойственности состоит в том, что для любого допустимого плана производства Х и любого вектора оценок ресурсов Y общая созданная стоимость не превосходит суммарной оценки ресурсов. Теорема 2: (критерий оптимальности Канторовича) Если для некоторых допустимых планов Экономическое содержание теоремы состоит в том, что план производства Х и вектор оценок ресурсов Y является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают. Теорема 3: (малая теорема двойственности) Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них. Теорема 4: Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: z( Между переменными двойственных задач можно установить соответствие, сопоставляя свободным переменным одной задачи базисные переменные другой. Опорному оптимальному плану исходной задачи соответствует опорный оптимальный план двойственной, который оказывается записанным с противоположными знаками в индексной строке последней симплексной таблицы. Пример 1: Решить исходную задачу линейного программирования, исходя из решения двойственной:
при Решение. Преобразуем систему ограничений следующим образом:
Составим двойственную задачу для данной:
при Решим полученную задачу симплексным методом. Преобразуем систему ограничений следующим образом:
Для полученной М-задачи составим симплексную таблицу.
Полученный план оптимальный. f=10 в (2, 0, 1, 0, 0, 0, 0) Найдем решение прямой задачи. Z=10 в (5, 1, 2)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |


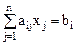 (
(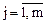 ),
),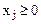 (
(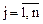 ).
).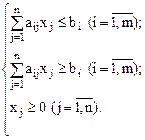

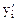 и
и  . Получим:
. Получим:
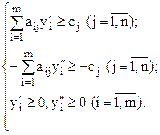
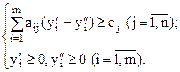
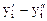 .
. 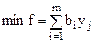
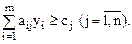

 (
(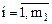 ),
),
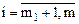 ),
),
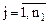 ),
),
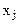 – любого знака (
– любого знака (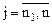 ).
).
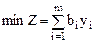 при
при
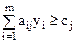 (
( (
(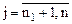 ),
),
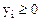 (
( – любого знака (
– любого знака (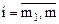 ).
).
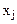 прямой задачи наложено условие неотрицательности, то j-тое условие системы ограничений двойственной задачи в виде неравенств и наоборот.
прямой задачи наложено условие неотрицательности, то j-тое условие системы ограничений двойственной задачи в виде неравенств и наоборот.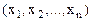 и Y=
и Y= 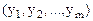 прямой и двойственной задачи линейного программирования справедливо неравенство:
прямой и двойственной задачи линейного программирования справедливо неравенство: .
.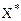 и
и 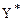 пары двойственных задач выполняется равенство z(
пары двойственных задач выполняется равенство z(