
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициентами при неизвестных целевой функции двойственной задачи являютсяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
!коэффициенты при неизвестных целевой функции исходной задачи Свободные члены системы ограничений исходной задачи Неизвестные исходной задачи Коэффициенты при неизвестных системы ограничений исходной задачи
Свободными членами системы ограничений двойственной задачи являются Неизвестные исходной задачи !коэффициенты при неизвестных исходной задачи Свободные члены исходной задачи Коэффициенты целевой функции исходной задачи
Если исходная ЗЛП была на максимум целевой функции, то двойственная задача будет Тоже на максимум Либо на максимум, либо на минимум И на максимум, и на минимум !на минимум
Если исходная ЗЛП была на минимум целевой функции, то двойственная задача будет !на максимум Либо на максимум, либо на минимум И на максимум, и на минимум Тоже на минимум
Если в сходной ЗЛП система ограничений в матричной форме имеет вид
!
Если в исходной ЗЛП система ограничений в матричной форме имеет вид
!
Пары двойственных задач называются симметричными, если в исходной задаче система ограничений задана в виде !системы неравенств системы уравнений матричного уравнения векторного уравнения
Пары двойственных задач называются несимметричными, если в исходной задаче система ограничений задана в виде системы неравенств !системы уравнений матричного неравенства векторного неравенства
В симметричной паре двойственных ЗЛП условие неотрицательности накладывается только на исходные переменные накладываются только на двойственные переменные !накладывается и на исходные, и на двойственные переменные не накладывается
В несимметричной паре двойственных ЗЛП условие неотрицательности !накладывается только на исходные переменные накладывается только на двойственные переменные накладывается и на исходные, и на двойственные переменные не накладывается ни на исходные, ни на двойственные переменные
Если целевая функция одной из пары двойственных задач не ограничена, то другая имеет решение !не имеет решения имеет единственное решение имеет бесконечное множество решений
Если система ограничений ЗЛП имеет вид Дополнительные переменные Основные переменные свободные члены !значения целевой функции
Если при решении ЗЛП симплексным методом на max целевой функции найдется оценка найден оптимальный план !ЗЛП не имеет решения надо решать ЗЛП другим методом поиск оптимального решения следует продолжить
Если при решении ЗЛП симплексным методом на min целевой функции найдется оценка надо продолжить поиск оптимального решения найден оптимальный план ЗЛП !ЗЛП не имеет решения надо решать ЗЛП другим методом
При решении ЗЛП на max целевой функции в симплекс – таблице с оптимальным планом все неположительны произвольны равны нулю !неотрицательны
При решении ЗЛП на min целевой функции в симплекс – таблице с оптимальным планом все !неположительны произвольны равны нулю неотрицательны
Тема 8. Транспортные задачи. Блокирование. Распределительные задачи
Если план транспортной задачи Х=
!
Модель транспортной задачи закрытая, если
!
Цикл в транспортной задаче – это замкнутая ломаная линия с горизонтальными и вертикальными звеньями, все вершины которой находятся в занятых клетках замкнутая ломаная линия с горизонтальными и вертикальными звеньями, все вершины которых находятся в свободных клетках замкнутая ломаная линия, одна вершина которой в занятой клетке, а остальные в свободных клетках !замкнутая ломаная линия с горизонтальными и вертикальными звеньями, одна вершина которой в свободной клетке, а остальные в занятых клетках
План транспортной задачи называется вырожденным, если число загруженных клеток меньше m+n-1 больше m+n-1 !равно m+n-1 равно m+n
Модель транспортной задачи является открытой, если !
не зависит от
Потенциалами транспортной задачи размерности (m×n) называются m+n чисел ui и vj, для которых выполняются условия !ui+vj=cij для занятых клеток ui+vj=cij для свободных клеток ui+vj=cij для первых двух столбцов распределительной таблицы ui+vj=cij для первых двух строк распределительной таблицы
Оценками транспортной задачи размерности (m+n) называются числа γij=cij-ui-vj, которые вычисляются для занятых клеток !для свободных клеток для первых двух строк распределительной таблицы для первых двух столбцов распределительной таблицы
Целевая функция транспортной задачи имеет вид
!
При составлении первоначального плана транспортной задачи по методу минимальной стоимости в первую очередь заполняются клетки расположенные по главной диагонали распределительной таблицы с максимальными тарифами !с минимальными тарифами расположенные в первых строках и столбцах распределительной таблицы
При решении транспортной задачи значение целевой функции должно от итерации к итерации увеличиваться увеличиваться или не меняться увеличиваться на !уменьшаться или не меняться
В клетках распределительной таблицы транспортной задачи располагаются только тарифы перевозок cij только планы перевозок xij !планы перевозок xij и соответствующие тарифы cij значения произведений cijxij
Если план транспортной задачи X=(xij)m×n является оптимальным, то оценки γij=cij-ui-vj удовлетворяют условиям γij <0 для всех клеток γij γij <0 для свободных клеток !γij
Распределительная таблица транспортной задачи это таблица, в которую записывается план задачи таблица, в которую записаны тарифы перевозок таблица, в которую записывается оптимальный план перевозок !таблица, в которую записаны план перевозок и тарифы перевозок
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид
!
Чтобы произвести блокировку некоторой клетки транспортной задачи, в этой клетке тариф изменяют на нуль удваивают !изменяют на достаточно большое число уменьшают в два раза
Число занятых клеток любого плана транспортной задачи должн быть равно m+n m+n-1 !m+n-1 m+n+1
Экономический смысл целевой функции транспортной задачи суммарный объем перевозок !суммарная стоимость перевозок суммарные поставки суммарные потребности
В целевой функции транспортной задачи коэффициенты прямых затрат коэффициенты полных затрат !стоимость перевозки одной тонны перевозок от i–ого поставщика к j–ому потребителю общая стоимость перевозки от i–ого поставщика к j–ому потребителю
В целевой функции транспортной задачи тарифы перевозок коэффициенты полных затрат коэффициенты прямых затрат !объем груза от i–ого поставщика к j–ому потребителю
В транспортной задаче сумма потенциалов ui+vj равна тарифу cij !занятых клеток всех незанятых клеток для любых клеток для первого ряда клеток
В транспортной задаче оценки γij вычисляются для занятых клеток для всех клеток !для незанятых клеток для клеток первого столбца
В транспортной задаче максимизируется объем перевозок !минимизируется общая стоимость перевозок минимизируется общий объем перевозок минимизируется объем холостого пробега транспорта
Элементы матрицы производительностей руб/час !шт/час руб шт
Элементы матрицы затрат руб шт/час !руб/шт шт/руб
В таблице задачи о загрузке оборудования каждая клетка содержит производительность станка, затраты на один час работы станка, объем перевозок !производительность станка, затраты на один час работы станка, время работы над j-ым изделием производительность станка, время работы над j-ым изделием коэффициент полных затрат, коэффициент прямых затрат, затраты на один час работы
В задаче о загрузке оборудования a1, a2…am – это плановое задание !время работы станков суточные объемы производства производительности станков
В задаче о загрузке оборудования b1, b2, …bn – это мощности станков коэффициенты прямых затрат коэффициенты полных затрат !плановые задания по выпуску изделий в штуках
В задаче о загрузке оборудования
!
В задаче о загрузке оборудования коэффициентом надежности коэффициентом полных затрат !индексом i–ого станка коэффициентом прямых затрат
В задаче о загрузке оборудования
приведенными к стандартным часам ресурсами !приведенными к стандартным часам плановыми заданиями приведенными к стандартным часам затратами приведенными к стандартным часам временами
В задаче о загрузке оборудования
приведенными к стандартным часам ресурсами !приведенными к стандартным часам затратами приведенными к стандартным часам временами приведенными к стандартным часам плановыми заданиями
В задаче о загрузке оборудования !приведенными к стандартным часам временем работы станков приведенными к стандартным часам затратами индексом i – го станка приведенными к стандартным часам плановыми заданиями
В приведенные затраты !приведенное время работы i – го станка по производству изделий вида j приведенные мощности станков приведенные ресурсы
Отрицательная оценка увеличивается на не изменяется !уменьшается на уменьшается на единицу
План транспортной задачи называется невырожденным, если число загруженных клеток !меньше m+n-1 больше m+n-1 равно m+n равно m+n-1
Дан план транспортной задачи
Неоптимальной будет клетка (2,2) (1,3) !(1,1) (2,3)
Дан план транспортной задачи
Этот план !невырожденный Открытый Вырожденный Оптимальный
Дан план транспортной задачи
Неоптимальной будет клетка (1,2) (2,1) (3,2) !(3,3)
Дана транспортная задача
Первоначальный план, найденный методом минимальной стоимости, имеет вид
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!
Дан план транспортной задачи
Значение целевой функции равно !750
Дан план транспортной задачи
этот план Невырожденный Открытый Отимальный !вырожденный
Дан план транспортной задачи
Цикл нужно строить для клетки (2,2) (2,1) !(1,1) (1,3)
Дана транспортная задача
План, найденный по методу двойного предпочтения, имеет вид
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!
Дана транспортная задача и дополнительное условие: третий поставщик должен полностью отправить свой груз.
Необходимо заблокировать клетку (1,3) (3,2) !(3,3) (2,3)
Дана транспортная задача c дополнительным условием, что перевозки от второго поставщика к третьему потребителю запрещены.
Необходимо заблокировать клетку (2,1) !(2,3) (2,2) (3,2)
Дана транспортная задача c дополнительным условием, что первый потребитель должен получить груз полностью.
Необходимо заблокировать клетку (3,1) (4,2) (3,2) !(4,1) Тема 9. Сетевое планирование и управление
Реальная работа - это работа, не требующая времени работа, не требующая ресурсов !работа, требующая затрат ресурсов и времени работа, требующая затрат ресурсов.
Полный резерв времени
!
Конечное событие сетевого графика – это событие, не имеющее входящих работ событие, имеющее несколько выходящих работ !событие, не имеющее выходящих работ событие, имеющее несколько входящих работ.
Начальное событие сетевого графика – это событие имеющее несколько входящих работ !не имеющее входящих работ не имеющее выходящих работ имеющее несколько выходящих работ.
Временной параметр самый ранний срок окончания работы самый поздний срок начала работы !самый ранний срок начала работы самый поздний срок окончания работы
Параметр поздний срок окончания работы !полный резерв времени на работу поздний срок начала работы свободный резерв времени.
Работа – ожидание !требует только время требует только ресурсы требует и время, и ресурсы не требует ни времени, ни ресурсов
Событие n-го ранга (n¹1) – это событие
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.16.251 (0.011 с.) |

 , то в двойственной ЗЛП она примет вид
, то в двойственной ЗЛП она примет вид




 и при этом все
и при этом все  , то
, то и при этом все
и при этом все 
 является оптимальным, то ему соответствует система
является оптимальным, то ему соответствует система  чисел, называемых потенциалами, для которых выполняются следующие условия
чисел, называемых потенциалами, для которых выполняются следующие условия для
для  ,
,  для
для 
 для
для 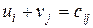 для
для  для
для 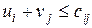 для
для  для
для 
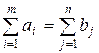




 и
и 


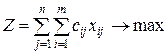




 0 для всех клеток
0 для всех клеток 0 для свободных клеток
0 для свободных клеток коэффициенты cij – это
коэффициенты cij – это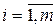 ,
,  для
для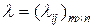 в
в 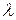 - задаче имеют размерность
- задаче имеют размерность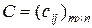 в
в 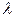 - задаче имеют размерности
- задаче имеют размерности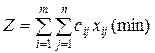
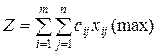
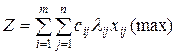
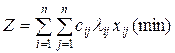
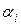 называется
называется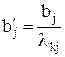 (
(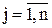 )называются
)называются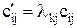 (
(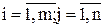 ) называются
) называются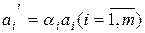 называются
называются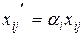 - это
- это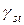 показывает, если перебросить в транспортной таблице в клетку
показывает, если перебросить в транспортной таблице в клетку 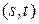 единицу груза, то затраты по перевозке груза
единицу груза, то затраты по перевозке груза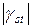

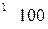

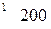
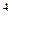
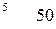
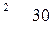
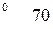
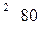
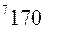
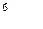
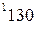
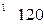

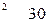

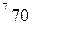
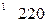
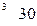
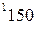

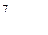



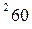
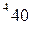
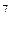
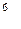
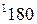
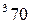
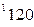
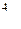
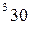
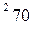
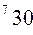
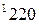
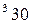
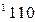
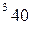
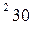
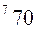
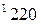
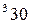
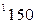
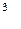
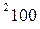
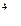
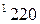
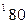
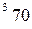
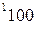
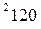
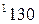
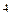
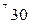
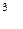
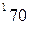
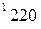
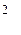
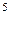
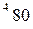
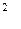
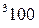
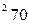
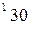
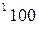
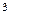
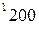


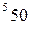
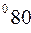


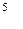
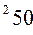
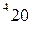
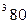
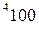
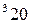
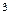
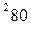
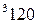
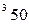
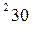
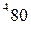
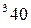
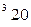
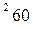
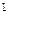


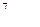


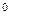
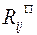 вычисляется по формуле
вычисляется по формуле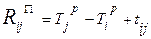
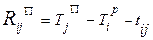
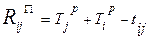
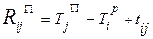
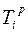 - это
- это


