
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В контрольный столбец 1-й таблицы Жордана – Гаусса записываетсяСодержание книги
Поиск на нашем сайте
Невырожденной Вырожденной !диагональной Треугольной
ТЕМА 3. Решение систем линейных уравнений методом Жордана – Гаусса.
Общим решением системы m линейных уравнений с n неизвестными называется решение, в котором свободные неизвестные произвольны !решение, в котором базисные неизвестные линейно выражаются через свободные неизвестные сумма частных решений этой системы сумма частных и базисных решений этой системы
Частным решением системы m линейных уравнений с n неизвестными называется !решение, полученное из общего решения, если свободным неизвестным придать произвольные значения решение, состоящее только из свободных неизвестных решение, в котором все компоненты – дробные частное от деления общего решения на базисное
При отыскании общего решения системы m линейных уравнений с n неизвестными методом Жордана – Гаусса в качестве разрешающего элемента выбирается элемент таблицы, удовлетворяющий условию элемент таблицы, удовлетворяющий условию !любой отличный от нуля элемент таблицы, кроме элементов столбца свободных членов и контрольного столбца любой элемент таблицы
Система m линейных уравнений с n неизвестными не имеет решений, если на некоторой итерации все элементы какой либо строки таблицы Жордана – Гаусса равны нулю две какие – либо строки таблицы Жордана – Гаусса одинаковы какой – либо из свободных членов !все элементы какой – либо строки таблицы Жордана – Гаусса, кроме свободного члена, равны нулю
Базисным решением системы m линейных уравнений с n неизвестными называется !решение, полученное из общего решения системы, в котором свободные неизвестные равны 0 решение, в котором базисные неизвестные произвольны решение, в котором свободные неизвестные произвольны система, приведенная к единичному базису
Если r – число базисных неизвестных, а n – общее число неизвестных в произвольной системе m линейных уравнений, то система имеет бесконечное множество решений при
!
Если дано матричное уравнение
!
Если в таблице Жордана – Гаусса !
Итерацией в методе Жордана - Гаусса называется расчет одной строки в таблице Жордана – Гаусса !расчет элементов одной таблицы Жордана – Гаусса вычисление элементов одного столбца в таблице Жордана – Гаусса вычисление элементов вводимой строки
Метод Жордана – Гаусса это нахождение производной нахождение разрешающего уравнения !последовательное исключение неизвестных нахождение разрешающего элемента
Если в таблице Жордана – Гаусса имеются две одинаковые строки, то их нужно сложить их нужно перемножить одну из них сложить со строкой, элементы которой отличаются !одну из них можно вычеркнуть
Единичным называется столбец таблицы Жордана – Гаусса, который состоит из единиц !одной единицы и остальных 0 двух единиц и нулей нулей
Переменная называется базисной, если в таблице Жордана – Гаусса столбец коэффициентов перед ней является нулевым отрицательным !единичным положительным
Если в таблице Жордана – Гаусса имеются две пропорциональные строки, то одну можно вычесть из другой их нужно сложить их нужно перемножить !одну из них нужно вычеркнуть
Переменная называется свободной, если в таблице Жордана – Гаусса столбец коэффициентов при ней нулевой !она не входит в столбец - базис столбец коэффициентов при ней состоит из единиц она входит в столбец - базис
Система m линейных уравнений с n неизвестными называется однородной, если свободные члены !равны 0 положительны отрицательны принимают любые значения
Матрица коэффициентов при неизвестных системы m линейных уравнений с n неизвестными квадратной диагональной !прямоугольной матрицей столбцом
Число частных решений равно числу базисных решений числу опорных решений числу допустимых решений !бесчисленному множеству решений
Переход от одного базисного решения к другому осуществляется путем !проведения еще одной итерации метода Жордана – Гаусса выбора разрешающей строки выбора разрешающего столбца проведения симплексных преобразований
Элементы вводимой строки в таблице Жордана – Гаусса находятся умножением элементов разрешающей строки предыдущей таблицы на (-1) делением элементов разрешающей строки предыдущей таблицы на (-1) !делением элементов разрешающей строки предыдущей таблицы на разрешающей элемент умножением элементов разрешающей строки предыдущей таблицы на разрешающий элемент
Число базисных решений произвольной системы m линейных уравнений с n неизвестными определяется !формулой числом уравнений числом неизвестных размерностью матрицы системы
Решение системы m линейных уравнений с n неизвестными, в котором базисные неизвестные линейно выражаются через свободные, называется частным допустимым !общим единственным
Систему можно решить матричным способом, если число уравнений не равно числу неизвестных !число уравнений равно числу неизвестных число уравнений меньше числа неизвестных число уравнений больше числа неизвестных
Решение, полученное из общего решения, если свободным неизвестным придать произвольные значения, называется допустимым опорным !частным единственным
Значение базисных переменных в таблице Жордана – Гаусса находится в вводимой строке !столбце контрольном столбце в разрешающей строке
Линейно зависимой Нелинейно зависимой Нелинейно независимой Линейно независимой
Если минимальной линейно независимой !максимальной линейно независимой минимальной линейно зависимой максимальной линейно зависимой
Всякая система векторов, содержащая нулевой вектор является линейно независимой нелинейно зависимой нелинейно независимой !линейно зависимой
Число векторов, входящих в любую максимальную линейно независимую подсистему векторов, называется порядком системы размером системы !рангом системы числом системы
Максимальное число линейно независимых векторов системы !из компонент векторов этой системы из квадратов компонент этой системы из кубов компонент этой системы из квадратных корней компонент этой системы
Рангом системы векторов называется число векторов, входящих в любую максимальную линейно зависимую подсистему !максимальную линейно независимую подсистему минимальную линейно зависимую подсистему минимальную линейно независимую подсистему
Максимальное число линейно независимых строк матрицы равно минимальному числу линейно независимых столбцов матрицы минимальному числу линейно зависимых столбцов матрицы максимальному числу линейно зависимых столбцов матрицы !максимальному числу линейно независимых столбцов матрицы
Любая совокупность n+1 векторов n–мерного векторного пространства !линейно зависима линейно независима образует базис нелинейно независима
Максимальное число линейно независимых строк матрицы равно размерности этой матрицы !рангу этой матрицы числу строк этой матрицы числу столбцов этой матрицы
Базисом n–мерного векторного пространства называется любая совокупность n+1 линейно независимых векторов этого же пространства n-1 линейно независимых векторов этого же пространства n(n-1) линейно независимых векторов этого же пространства !n линейно независимых векторов этого же пространства
Любой вектор n–мерного векторного пространства можно представить как нелинейную комбинацию векторов базиса !линейную комбинацию векторов базиса сумму векторов базиса произведение векторов базиса
Система нулевых векторов n–мерного векторного пространства зависимых векторов n –мерного векторного пространства !единичных векторов n–мерного векторного пространства независимых векторов (n+1)–мерного векторного пространства
высотой вектора шириной вектора размером вектора !длиной вектора
Числа числами вектора !компонентами вектора номерами вектора неизвестными вектора
Любой вектор n–мерного пространства можно представить как линейную комбинацию векторов базиса множеством способов n способами n-1 способами !единственным образом
Рангом матрицы A называется число r такое, что у матрицы существует !хотя бы один отличный от нуля минор r–го порядка и равны нулю все миноры более высокого порядка(³r+1) хотя бы один отличный от нуля минор r+1–го порядка и равны нулю все миноры более высокого порядка не более одного отличного от нуля минора r–го порядка и равны нулю все миноры более высокого порядка не более одного отличного от нуля минора r+1–го порядка и равны нулю все миноры более высокого порядка
Если r-ранг матрицы А, то отличный от нуля минор r–го порядка называется основным минором матрицы минимальным минором матрицы !базисным минором матрицы ненулевым минором матрицы
Какое число линейно независимых векторов системы Минимальное Бесконечное !равно n Максимальное
Максимальное число линейно независимых столбцов матрицы равно размерности этой матрицы числу строк этой матрицы числу столбцов этой матрицы !рангу этой матрицы
Система векторов называется линейно независимой, если соотношение
!
Число векторов, входящих в любую максимальную линейно независимую подсистему векторов, называется порядком системы размерностью системы числом системы !рангом системы
Указать совокупность векторов n – мерного векторного пространства, которая заведомо является линейно зависимой совокупность n-2 векторов совокупность n-1 векторов совокупность n векторов !совокупность n+1 векторов
Для линейной независимости системы из n n – мерных векторов необходимо и достаточно, чтобы определитель, составленный из компонент векторов этой системы равнялся 0 !был отличен от 0 существовал не существовал
Система из пяти 4 – х мерных векторов не существует линейно независима !линейно зависима образует базис
Если (8;-3) (6;-2) !5
Система векторов !образует базис не образует базиса линейно зависима вырождена
Компоненты вектора (1:-1) (2;2) !(3;-1) (3;5)
Векторы
!
ТЕМА 5. Неотрицательные решения систем линейных уравнений. Симплексные преобразования
Опорными решениями называются !неотрицательные базисные решения неотрицательные решения линейно-независимые решения положительные решения
Если в какой-либо строке таблицы Гаусса свободный член положителен, а все остальные элементы строки отрицательны или равны 0, то система имеет единственное решение !система не имеет неотрицательных решений система имеет неединственное решение система имеет бесконечно много решений
Опорные решения отрицательны положительны !неотрицательны нулевые
Неотрицательные решения системы линейных уравнений находятся с помощью линейных преобразований алгебраических преобразований матричных преобразований !симплексных преобразований
При симплексных преобразованиях свободные члены уравнений должны быть !неотрицательными отрицательными положительными нулевыми
При симплексных преобразованиях за разрешающий столбец выбирается такой, в котором есть хотя бы один 0 !есть хотя бы одно положительное число есть хотя бы одно отрицательное число нет ни одного нуля
При симплексных преобразованиях элементы таблицы вычисляются по формулам Крамера Форда !Жордана-Гаусса Беллмана
При симплексных преобразованиях расчет таблиц продолжается до тех пор, пока все правые части уравнений не станут положительными одна неизвестная не будет выражена через все остальные неизвестные в разрешающем столбце все числа не станут неотрицательными !система не будет приведена к единичному базису
Переход от одного опорного решения к другому осуществляется с помощью линейных преобразований !симплексных преобразований алгебраических преобразований матричных преобразований
Количество опорных решений всегда равно количеству базисных решений всегда меньше количества базисных решений !меньше или равно количеству базисных решений равно числу уравнений
При симплексных преобразованиях разрешающий элемент расположен на пересечении разрешающей строки и столбца свободных членов разрешающего столбца и строки с неотрицательными членами разрешающей строки и первого столбца !разрешающей строки и разрешающего столбца
Если правые части уравнений неотрицательны, то после симплексных преобразований они !останутся неотрицательными станут строго положительными могут быть отрицательными могут быть любого знака.
При симплексных преобразованиях число строк таблицы равно числу неизвестных !рангу системы числу базисных решений всегда двум
С помощью симплексных преобразований находятся ненулевые решения системы уравнений частные решения системы уравнений !опорные решения системы уравнений отрицательные решения системы уравнений
Опорное решение – это ненулевое решение частное решение любое решение !базисное неотрицательное решение
Разрешающий элемент в симплексных преобразованиях Положительный !неотрицательный Отрицательный Нулевой
При получении решения системы уравнений с помощью симплексных преобразований количество итерации равно количеству переменных количеству ненулевых элементов разрешающего столбца количеству нулевых элементов разрешающей строки !количеству базисных переменных
Если при симплексных преобразованиях разрешающий элемент находится в строке с номером !
Если при симплексных преобразованиях разрешающий элемент находится в строке с номером
!
Решения систем линейных уравнений, которые принимают неотрицательные значения называются недопустимыми !допустимыми нулевыми нормальными
Совокупность всевозможных допустимых решений системы линейных уравнений называется областью определения областью решений !областью допустимых решений множеством неизвестных
Последовательное применение симплексных преобразований позволяют определить все отрицательные решения системы !опорные решения системы нулевые решения системы действительные решения системы
Указать среди базисных решений опорное
!
Указать вариант, в котором свободные члены системы уравнений могут являться результатом симплексных преобразований, если до них они были неотрицательными (-2, 5, -6, -4) (-1, 3, 4, -6) !(4, 5, 7, 3) (3, -2, 5, 1)
Какое количество опорных решений не может соответствовать перечисленным ниже числам, если число базисных решений равно десяти !11
Если все свободные члены системы неотрицательны, то после каких преобразований они останутся неотрицательными нормальных !симплексных прямых обратных
Решения систем линейных уравнений называются допустимыми, если они принимают отрицательные значения нулевые значения !неотрицательные значения бесконечные значения
Если система уравнений приведена к единичному базису и при этом ее свободные члены неотрицательны, то соответствующее системе решение является нулевым !опорным нормальным обратным
При симплексных преобразованиях в качестве разрешающего уравнения выбирается то уравнение, для которого отношение свободного члена к положительному элементу разрешающего столбца наибольшее !наименьшее равно нулю больше нуля
Система уравнений приведена к единичному базису. Ее решение является опорным, если свободные члены отрицательные нулевые !неотрицательные неположительные
Указать вариант, в котором свободные члены систем уравнений не могут являться результатом симплексных преобразований, если до них они были неотрицательными !(2, -5, 6, -4) (1, 3, 2, 6) (4, 1, 5, 3) (3, 2, 5, 1,)
При каком преобразовании разрешающий столбец выбирается так, чтобы он имел хотя бы один положительный элемент? при обратном !при симплексном при нормальном при прямом
В качестве какого уравнения выбирается уравнение системы, для которого отношение свободного члена к положительному элементу разрешающего столбца наименьшее нормального линейного !разрешающего нелинейного
Если система уравнений приведена к единичному базису и при этом хотя бы один из ее свободных членов отрицательный, то соответствующее системе решение не является нормальным !опорным базисным обратным
Указать среди базисных решение, которое не является опорным
!
Переход от одного опорного решения к другому называется однократной заменой !однократным замещением однократной перестановкой однократным перемещением
При симплексных преобразованиях разрешающая строка отыскивается по правилу
!
Если в i – м уравнении системы линейных уравнений все частных решений базисных решений общих решений !неотрицательных решений
Симплексные преобразования применяются для отыскании неотрицательных векторов определителей !решений системы уравнений коэффициентов системы уравнений
Если в i – м уравнении системы линейных уравнений свободный член Запасы i – го вида сырья !максимальное количество сырья, необходимое для производства 1 единицы продукции Стоимость сырья i – го вида Неизвестные исходной задачи Неизвестные исходной задачи !коэффициенты при неизвестных исходной задачи Тоже на максимум И на максимум, и на минимум !на минимум
И на максимум, и на минимум Тоже на минимум
Если в сходной ЗЛП система ограничений в матричной форме имеет вид
!
Если в исходной ЗЛП система ограничений в матричной форме имеет вид
!
Пары двойственных задач называются симметричными, если в исходной задаче система ограничений задана в виде !системы неравенств системы уравнений матричного уравнения векторного уравнения
Пары двойственных задач называются несимметричными, если в исходной задаче система ограничений задана в виде системы неравенств !системы уравнений матричного неравенства векторного неравенства
В симметричной паре двойственных ЗЛП условие неотрицательности накладывается только на исходные переменные накладываются только на двойственные переменные !накладывается и на исходные, и на двойственные переменные не накладывается
В несимметричной паре двойственных ЗЛП условие неотрицательности !накладывается только на исходные переменные накладывается только на двойственные переменные накладывается и на исходные, и на двойственные переменные не накладывается ни на исходные, ни на двойственные переменные
Если целевая функция одной из пары двойственных задач не ограничена, то другая имеет решение !не имеет решения имеет единственное решение имеет бесконечное множество решений
Если система ограничений ЗЛП имеет вид Дополнительные переменные Основные переменные свободные члены !значения целевой функции
Если при решении ЗЛП симплексным методом на max целевой функции найдется оценка найден оптимальный план !ЗЛП не имеет решения надо решать ЗЛП другим методом поиск оптимального решения следует продолжить
Если при решении ЗЛП симплексным методом на min целевой функции найдется оценка надо продолжить поиск оптимального решения найден оптимальный план ЗЛП !ЗЛП не имеет решения надо решать ЗЛП другим методом
При решении ЗЛП на max целевой функции в симплекс – таблице с оптимальным планом все неположительны произвольны равны нулю !неотрицательны
При решении ЗЛП на min целевой функции в симплекс – таблице с оптимальным планом все !неположительны произвольны равны нулю неотрицательны
Тема 8. Транспортные задачи. Блокирование. Распределительные задачи
Если план транспортной задачи Х=
!
Модель транспортной задачи закрытая, если
!
Цикл в транспортной задаче – это замкнутая ломаная линия с горизонтальными и вертикальными звеньями, все вершины которой находятся в занятых клетках замкнутая ломаная линия с горизонтальными и вертикальными звеньями, все вершины которых находятся в свободных клетках замкнутая ломаная линия, одна вершина которой в занятой клетке, а остальные в свободных клетках !замкнутая ломаная линия с горизонтальными и вертикальными звеньями, одна вершина которой в свободной клетке, а остальные в занятых клетках
План транспортной задачи называется вырожденным, если число загруженных клеток меньше m+n-1 больше m+n-1 !равно m+n-1 равно m+n
Модель транспортной задачи является открытой, если !
не зависит от
Потенциалами транспортной задачи размерности (m×n) называются m+n чисел ui и vj, для которых выполняются условия !ui+vj=cij для занятых клеток ui+vj=cij для свободных клеток ui+vj=cij для первых двух столбцов распределительной таблицы ui+vj=cij для первых двух строк распределительной таблицы
Оценками транспортной задачи размерности (m+n) называются числа γij=cij-ui-vj, которые вычисляются для занятых клеток !для свободных клеток для первых двух строк распределительной таблицы для первых двух столбцов распределительной таблицы
Целевая функция транспортной задачи имеет вид
!
При составлении первоначального плана транспортной задачи по методу минимальной стоимости в первую очередь заполняются клетки расположенные по главной диагонали распределительной таблицы с максимальными тарифами !с минимальными тарифами расположенные в первых строках и столбцах распределительной таблицы
При решении транспортной задачи значение целевой функции должно от итерации к итерации увеличиваться увеличиваться или не меняться увеличиваться на !уменьшаться или не меняться
В клетках распределительной таблицы транспортной задачи располагаются только тарифы перевозок cij только планы перевозок xij !планы перевозок xij и соответствующие тарифы cij значения произведений cijxij
Если план транспортной задачи X=(xij)m×n является оптимальным, то оценки γij=cij-ui-vj удовлетворяют условиям γij <0 для всех клеток γij γij <0 для свободных клеток !γij
Распределительная таблица транспортной задачи это таблица, в которую записывается план задачи таблица, в которую записаны тарифы перевозок таблица, в которую записывается оптимальный план перевозок !таблица, в которую записаны план перевозок и тарифы перевозок
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид
!
Чтобы произвести блокировку некоторой клетки транспортной задачи, в этой клетке тариф изменяют на нуль удваивают !изменяют на достаточно большое число уменьшают в два раза
Число занятых клеток любого плана транспортной задачи должн быть равно m+n m+n-1 !m+n-1 m+n+1
Экономический смысл целевой функции транспортной задачи суммарный объем перевозок !суммарная стоимость перевозок суммарные поставки суммарные потребности
В целевой функции транспортной задачи коэффициенты прямых затрат коэффициенты полных затрат !стоимость перевозки одной тонны перевозок от i–ого поставщика к j–ому потребителю общая стоимость перевозки от i–ого поставщика к j–ому потребителю
В целевой функции транспортной задачи тарифы перевозок коэффициенты полных затрат коэффициенты прямых затрат !объем груза от i–ого поставщика к j–ому потребителю
В транспортной задаче сумма потенциалов ui+vj равна тарифу cij | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |








 , то его решение определяется по формуле
, то его решение определяется по формуле



 - разрешающий элемент, то элемент
- разрешающий элемент, то элемент  находится по формуле (правило прямоугольника)
находится по формуле (правило прямоугольника)


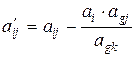

 является
является

 – линейно зависимая система векторов, а
– линейно зависимая система векторов, а  (r£n) - такая ее линейно независимая подсистема векторов, к которой нельзя присоединить ни одного вектора системы, не нарушив линейной независимости, то эта подсистема называется
(r£n) - такая ее линейно независимая подсистема векторов, к которой нельзя присоединить ни одного вектора системы, не нарушив линейной независимости, то эта подсистема называется , составленной
, составленной называется системой
называется системой называется
называется , определяющие вектор
, определяющие вектор  , называются
, называются справедливо лишь в случае, когда
справедливо лишь в случае, когда



 ,
,  то произведение
то произведение  равно
равно ,
,  ,
, 
 в базисе
в базисе  ,
,  , где
, где  ,
,  , равны
, равны и
и  равны между собой, если
равны между собой, если



 и в столбце с номером k, то новые значения правых частей уравнения подсчитываются по формуле
и в столбце с номером k, то новые значения правых частей уравнения подсчитываются по формуле



 вычисляется по формуле
вычисляется по формуле




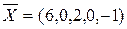

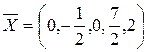







 ,
,  , то система не имеет
, то система не имеет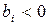 , то
, то , то в двойственной ЗЛП она примет вид
, то в двойственной ЗЛП она примет вид




 и при этом все
и при этом все  , то
, то и при этом все
и при этом все 
 является оптимальным, то ему соответствует система
является оптимальным, то ему соответствует система  чисел, называемых потенциалами, для которых выполняются следующие условия
чисел, называемых потенциалами, для которых выполняются следующие условия для
для  ,
,  для
для 
 для
для 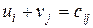 для
для  для
для 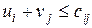 для
для  для
для 
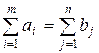




 и
и 


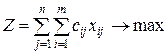




 0 для всех клеток
0 для всех клеток 0 для свободных клеток
0 для свободных клеток коэффициенты cij – это
коэффициенты cij – это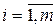 ,
, 


