
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В задача об оптимальном распределении ресурсов свободные члены в системе ограничений - этоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Запасы i – го вида сырья !максимальное количество сырья, необходимое для производства 1 единицы продукции Стоимость сырья i – го вида Прибыльот реализации i – го вида продукции
ТЕМА 7. Симплексный метод решения ЗЛП. Основные теоремы. Двойственные ЗЛП.
План X=(х1, х2,…хm, 0,…,0) ЗЛП на min будет оптимальным, если справедливы условия для j= Zj-Cj>0 !Zj-Cj£0 Zj-Cj³0 Zj-Cj=0
План X=(х1, х2,…хm, 0,…,0) ЗЛП на max будет оптимальным, если справедливы условия для j= !Zj-Cj³0 Zj-Cj<0 Zj-Cj=0 Zj-Cj£0
Разрешающий столбец при решении ЗЛП на max целевой функции выбирается исходя из условия
! любой столбец коэффициентов при неизвестных
Разрешающий столбец при решении ЗЛП на min целевой функции выбирается исходя из условия
!
Значение целевой функции в таблице с оптимальным планом находится на пересечении строки оценок со столбцом коэффициентов при х1 на пересечении строки оценок со столбцом в столбце коэффициентов при хn !на пересечении строки оценок со столбцом первоначального базиса
Оптимальным планом ЗЛП называется решение системы ограничений базисное решение системы ограничений опорный план !опорный план, приводящий к максимуму или минимуму целевой функции
ЗЛП решается симплексным методом, если в ЭММ ЗЛП в каноническом виде матрица коэффициентов системы ограничений !содержит единичную подматрицу не содержит единичной подматрицы содержит нулевую подматрицу не содержит нулевой подматрицы
Значения базисных переменных оптимального плана ЗЛП находятся в строке оценок последнем столбце !столбце первой строке
При решении ЗЛП симплексным методом свободные члены системы ограничений должны быть £ 0 !³ 0 = 0 < 0
При решении ЗЛП симплексным методом разрешающая строка выбирается по правилу
!
При решении ЗЛП симплексным методом оценки первой строке второй строке !(m+1)–й строке последнем столбце
При составлении симметричной пары двойственных задач, если исходная ЗЛП
!!!!!!!!!!!!!!!!!! !
При решении прямой ЗЛП решение двойственной задачи в симплекс – таблице с оптимальным планом получается на пересечении столбца свободных членов и строки оценок на пересечении последнего столбца и строки оценок !на пересечении строки оценок и столбцов, соответствующих начальному базису ЗЛП на пересечении первой строки и столбцов, соответствующих начальному базису ЗЛП.
Если i – е ограничение прямой ЗЛП обращается в строгое неравенство, то соответствующая компонента двойственной задачи не равна нулю !равна нулю положительна отрицательна
Если j – е ограничение двойственной задачи обращается в строгое неравенство, то соответствующая компонента прямой ЗЛП отрицательна положительна не равна нулю !равна нулю
Если одна из пары двойственных задач обладает оптимальным планом, то другая !имеет оптимальное решение и не имеет решения и имеет оптимальное решение и не имеет решения и
Если исходная ЗЛП имеет вид
!
Если исходная ЗЛП имеет вид
!
Если исходная ЗЛП имеет вид
!
Если исходная ЗЛП имеет вид !
Опорным планом ЗЛП называется неотрицательное решение системы ограничений базисное решение системы ограничений неотрицательное решение целевой функции !базисное неотрицательное решение системы ограничений
Если множество наряду со своими точками содержит и отрезок, соединяющий любые его две точки, то оно называется вогнутым !выпуклым полным ограниченным
Множество планов ЗЛП полно вогнуто !выпукло не ограниченно
Если при решении ЗЛП на максимум для некоторого фиксированного j найдется оценка оптимальным !неоптимальным отрицательным недопустимым
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 693; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.006 с.) |











 находятся в симплекс – таблице в
находятся в симплекс – таблице в ,
,  ,
,  , то двойственная задача имеет вид
, то двойственная задача имеет вид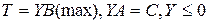


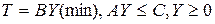


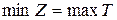 или
или 
 или
или 
 или
или 




 ,
,  ,
, 

 ,
, 





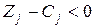 , то опорный план является
, то опорный план является


