
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономический смысл задачи, двойственной к задаче оптимального использования ресурсов.Содержание книги
Поиск на нашем сайте
Экономический смысл задачи, двойственной к задаче оптимального использования ресурсов. Необходимо найти такие «цены» на ресурсы, чтобы общая стоимость используемых ресурсов была минимальной. План произ-ва Х и набор оценок ресурсов У оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная, при известных заранее ценах продукции равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов yi. Для всех же других планов Х и У обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов:f(X) < g(Y}, т. е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит величина g(Y) - f(X) характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных Оценок ресурсов. Из 1-ой теоремы двойственности => при оптимальной производственной программе и векторе оценок ресурсов производственные потери равны нулю. =При моделировании экономич систем и процессов, когда хар=р системы до конца не изучен, или же система сложная, прибегают к упрощению модели и представлению ее в виде линейной (прямой или обратной). Исходная модель предполагает, сколько и какой продукции необходимо изготовить с заданной стоимостью cj (j=
Оценка точности модели кривой Роста, выбор наилучшей кривой роста. Точность моделей характеризуется величиной отклонения выхода модели от реального значения моделируемой переменной (экономич показателя). Для показателя, представленного временным рядом, точность определяется как разность между значением фактического уровня временного ряда и его оценкой полученной расчетным методом с использованием модели. В качестве стат показателя можно применять среднюю относительную ошибку аппроксимации.
Графический метод решения задачи линейного программирования. Если в задаче линейного программирования ограничения заданы в виде неравенств с двумя переменными, то задача может быть решена графически.. Стандартная форма ЛП: 3.линия уровня
Предварительный анализ временных рядов. Вычисление количественных характеристик развития экономических процессов Традиционными показателями, характеризующими развитие экономических процессов, были и остаются показатели роста и прироста. Для хар-ки динамики изменения экономич показателей все чаще используется понятие автокорреляции, которая харак-ует не только взаимозависимост уровней одного и того же ряда, относящихся к разным моментам наблюдений, но и степень устойчивости развития процесса во времени, величину оптимального периода прогнозирования и т.п
Основные понятия теории игр, игры с природой. Теория игр - математич теория конфликтных ситуаций. В игре могут сталкиваться интересы двух (игра парная) или нескольких (игра множественная) противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалиции, то игра называется коалиционной; если таких коалиций две, то игра сводится к парной. =На промышленных предприятиях теория игр может применяться для выбора оптимальных решений, например, при создании рациональных запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, и сокращения запасов в целях минимизации затрат на их хранение. 1.определенность в формулировании их условий (правил игры); 2. установления количества игроков, 3.выявления возможных стратегий игроков, 4.возможных выигрышей (проигрыш понимается как отрицательный выигрыш). Важным элементом в условии игровых задач является стратегия. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы – чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные. Одним из основных видом игр является матричные игры, которыми называются парные игры с нулевой суммой (один игрок выигрывает столько, сколько проигрывает другой) при условии, что каждый игрок имеет конечное число стратегий. Парная игра задается матрицей А=аij - которая называется матрица игры или платежная матрица.
Основные понятия о системах массового обслуживания, примеры их применения. Системы массового обслуживания – это системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, с другой – происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: 1.Источник требований, 2.Входящий поток требований, 3.Очередь, 4.Обслуживающие устройства (каналы обслуживания), 5.Выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания. Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. Например: 1.Определить в организации торговли оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и др.2.Для складов или баз снабженческо-сбытовых организаций установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными.
Экономический смысл задачи, двойственной к задаче оптимального использования ресурсов. Необходимо найти такие «цены» на ресурсы, чтобы общая стоимость используемых ресурсов была минимальной. План произ-ва Х и набор оценок ресурсов У оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная, при известных заранее ценах продукции равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов yi. Для всех же других планов Х и У обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов:f(X) < g(Y}, т. е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Значит величина g(Y) - f(X) характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных Оценок ресурсов. Из 1-ой теоремы двойственности => при оптимальной производственной программе и векторе оценок ресурсов производственные потери равны нулю. =При моделировании экономич систем и процессов, когда хар=р системы до конца не изучен, или же система сложная, прибегают к упрощению модели и представлению ее в виде линейной (прямой или обратной). Исходная модель предполагает, сколько и какой продукции необходимо изготовить с заданной стоимостью cj (j=
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.106 (0.01 с.) |

 ) и при заданных ресурсах bi (i=
) и при заданных ресурсах bi (i=  ) и получить максимальную прибыль в стоимостном выражении. Двойственная (обратная) задача предполагает оценку стоимости единицы каждого из ресурсов, чтобы при заданном количестве ресурсов bi и стоимости единицы продукции cj минимизировать общую стоимость затрат.
) и получить максимальную прибыль в стоимостном выражении. Двойственная (обратная) задача предполагает оценку стоимости единицы каждого из ресурсов, чтобы при заданном количестве ресурсов bi и стоимости единицы продукции cj минимизировать общую стоимость затрат. åcx = åby
åcx = åby где n- кол-во уровней ряда,
где n- кол-во уровней ряда,  - оценка уровней ряда по модели,
- оценка уровней ряда по модели,  - среднее арифметическое значение уровней ряда. Если ошибка, вычисленная по формуле, не превосходит 15%, точность модели считается приемлемой. На основании этого можно сделать выбор из нескольких адекватных трендовых моделей экономической динамики наиболее точной.
- среднее арифметическое значение уровней ряда. Если ошибка, вычисленная по формуле, не превосходит 15%, точность модели считается приемлемой. На основании этого можно сделать выбор из нескольких адекватных трендовых моделей экономической динамики наиболее точной. ,
,  , i=1,2,…m,
, i=1,2,…m,  , j=1,2,…n. этапы: 1.строится многоугольная ОДР. 2.строится вектор градиент целевой функции (ЦФ) в какой-нибудь точке х0, принадлежащей ОДР
, j=1,2,…n. этапы: 1.строится многоугольная ОДР. 2.строится вектор градиент целевой функции (ЦФ) в какой-нибудь точке х0, принадлежащей ОДР - прямая, перпендикулярная вектору градиенту, передвигается в направлении этого вектора в случае максимизации
- прямая, перпендикулярная вектору градиенту, передвигается в направлении этого вектора в случае максимизации 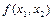 до тех пор, пока не покинет предела ОДР. Предельная точка или точки области при этом движении и является точкой максимума
до тех пор, пока не покинет предела ОДР. Предельная точка или точки области при этом движении и является точкой максимума  .. 4.для нахождения координат точки максимума достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение
.. 4.для нахождения координат точки максимума достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение  , найденное в получаемой точке, является максимальным. При минимизации функции
, найденное в получаемой точке, является максимальным. При минимизации функции 


