Общая запись оптимизационной ЭММ (задача оптимального программирования). Основные элементы и понятия.

Оптимизационные модели отражают в матем форме смысл экономической задачи, и отличительной особенностью этих моделей является наличие условия нахождения оптимального ре­шения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяю­щих условиям задачи, и обеспечивают выбор оптимального реше­ния, отвечающего критерию оптимальности.=В общем виде математическая постановка задачи матем программирования состоит в определении наибольшего или наименьшего значения целевой функции f (х₁, х₂,..., х_n) при условиях g_i(х₁, х₂,..., х_n) £ b_i; (i =1,2,…m), где f и g_i; – заданные функции, а b_i – некоторые действительные числа. =задачи математического программирования делятся на задачи линейного и нелинейного программирования. если все функции f и g_i линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.

В общем виде задача линейного программирования (ЗЛП) ставится так:

Найти вектор , максимизирующий линейную форму

(1)и удовле-щий условиям

(3)Линейная (2)

функция называется целевой функцией задачи. Условия (2) называются функциональными, а (3) - прямыми ограничениями задачи.

Вектор , компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП. Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию f(x), называется оптимальным планом задачи

где - оптимальное решение ЗЛП. =Реализовать на практике принцип оптимальности это значит разработать и получить решение по модели: max(min) максимизировать или минимиз-ать функцию f(x) при ограничениях, где f(x1,x2,…,xn) – математич запись критерия оптимальности -ЦФ. Max(min) f(x)=f(x1,x2,…,xn),x є D.

Обычно, приведенную модель записывают в виде:

Max(min) f(x1,x2,…,xn) (1) - ЦФ

g1(x1,x2,…xn) {≤, =, ≥ } b1

g2(x1,x2,…xn) {≤, =, ≥ } b2 - (2)-функциональные

gn(x1,x2,…xn) {≤, =, ≥ } bn

xi ≥ 0, i=1,¯ n - (3)прямые ограничения

 

 

Матрица коэффициентов полных материальных затрат, способы ее определения. Матричная форма модели Леонтьева (E-A)X=Y. По ней можно определить объемы валовой продукции отраслей X1,X2,…,Xn по заданным объемам конечной продукции: X=(E-A)ˉ¹ Y X=BY B=(E-A)ˉ¹. Если определитель матрицы (Е-А) не равен 0, то сущ обратная к ней матрица. В=(Е-А) ^-1 Элементы bij обратной матрицы B=(E-A)ˉ¹ называются коэффициентами полных (материальных) затрат. Это затраты i-той отрасли на каждый рубль конечной продукции отрасли j. Матрицу В называют матрицей коэффициентов полных затрат.

 

Определение объемов валовой и конечной продукции по модели Леонтьева С помощью этой модели можно выполнять три вида плановых расчетов: -- задавая для каждой отрасли величины валовой продукции (Xi) можно определить объемы конечной продукции каждой отрасли: Y=(E-A)X -- задавая величины конечной продукции всех отраслей (Yi) можно определить величины валовой продукции каждой отрасли (Xi): X=(E-A)^-1 Y

 

Матрица прямых материальных затрат, ее продуктивность. Признаки продуктивности По ЭММ Леонтьева (Е-А)X=Y можно определить объемы валовой продукции отрасли Х1, Х2, …, Хn по заданным объемам конечной продукции: Х = (Е-А)‾¹ Y; X=BY, B=(E-A)‾¹. Элементы Bij обратной матрицы B = (E-A)‾¹ называются коэффициентами полных (материальных) затрат, т.е. это затраты i-й отрасли на каждый рубль конечной продукции отрасли j. Соответственно матрицу В называют матрицей коэффициентов полных затрат, а матрицу А – матрицей коэффициентов прямых затрат. Матрицу неотрицательную А будем называть продуктивной если сущ такой неотрицательный вектор X>=0, что X>AX. Это условие означает существование положительного вектора конечной продукции Y>0 для модели межотраслевого баланса. Для того чтобы матрица коэф прямых материал затрат была продуктивной необходимо и достаточно чтобы выполнялось одно из перечисленных условий:-- матрица (Е-А) необратима, т.е. сущ обратная матрица (Е-А)^-1 >=0

-- сходится матричный ряд Е + А + А² + … + =∑А®, причем ∑А®=(Е-А)‾¹ -- положительны все главные миноры матрицы (Е – А) (т.е. определители матрицы образованные элементами первых строк и первых столбцов этой матрицы)-- максимальное собственное число матрицы А меньше 1. Собственными значениями (числами) квадратной матрицы А называются корни (решения) характеристического уравнения | А-λЕ |=0.

 

Эконом-математ модель межотраслевого стоимостного а (модель Леонтьева) Алгебраическая теория анализа модели «затраты-выпуск» сводится у решению системы линейных уравнений, в которых параметрами являются коэффициенты затрат на произ-во продукции. Пусть весь производственный сектор народного хозяйства разбит на n “чистых» отраслей. Чистая отрасль- это условное понятие – некоторая часть народного хозяйства, более или менее цельная. 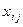Пусть - объем продукции отрасли i, расходуемой в отрасли j; - объем производства отрасли I за данный промежуток времени (валовый выпуск); 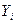- объем потребления продукции отрасли i в непроизводственной сфере (объем конечного потребления); условно чистая продукция, которая включает оплату труда, чистый доход и амортизацию. Единицы измерения указанных величин могут быть натуральными или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли Валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли: Запись в матричной форме: Х = АХ + Y, где А=(Аij) размерностью n*n Именно в этих двух формах записи и используется ЭММ межотраслевого баланса, которую называют моделью Леонтьева. Элементы Аij матрицы А называют коэффициентами прямых (материальных) затрат. Это – затраты i-й отрасли на единицу (рубль) валовой продукции j-й отрасли. В матричной форме модель Леонтьева записывается Х-АХ=Y или (Е-А)Х=Y.