
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура временных рядов экономических показателейСодержание книги
Поиск на нашем сайте Временной ряд- это набор чисел, призванный к последовательным, обычно равноотстоящим моментам времени. Числа, составляющие временной ряд и получающиеся в результате наблюдения за ходом некоторого процесса, называются уровнями временного ряда, или элементами. Интервал между двумя последовательными моментами времени называют тактом (шагом, квантом). Под длиной временного ряда понимают количество входящих в него уровней n. Временной ряд обычно обозначают Детерминирующая составляющая может содержать следующие структурные компоненты. 1. Тренд, или тенденция
Требования, предъявляемые к исходной информации при моделировании экономических процессов на основе временных рядов. Сопоставимость достигается в результате одинакового подхода к наблюдениям на разных этапах формирования динамического ряда. Уровни во временных рядах должны иметь одинаковые: единицы измерения, шаг наблюдений, интервал времени, методику расчета, элементы. Однородность данных означает отсутствие сильных изломов тенденций, а также аномальных наблюдений. Устойчивость характеризуется преобладанием закономерности над случайностью в изменении уровней ряда. Требование полноты данных обуславливается тем, что закономерность может обнаруживаться лишь при наличии минимально допустимого объема наблюдений.
Каноническая форма записи ЗЛП. Способы приведения ЗЛП к каноническому виду Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи к каноническому виду задачи линейного программирования. Под канонической формой ЗЛП понимают задачу сформулированную на максимум, все ограничения которой представлены уравнениями и все переменные не отрицательные. Для приведения задачи к КЗЛП в ограничения представленные неравенствами вводят дополнительные переменные со знаком +, если ограничение имеет вид неравенства <=, и со знаком - если ограничения имеют вид неравенства >=.
Выявление и устранение аномальных наблюдений во временных рядах. Для диагностики аномальных наблюдений разработаны различные критерии, например метод Ирвина. Для всех или только подозреваемых в аномальности наблюдений вычисляется величина
Задачи дискретной (целочисленной) оптимизации, пример(постановка задачи и ЭММ). Задача целочисленного программирования – это задача в которой все или некоторые переменные должны принимать целые значения. В этом случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей ЛП. Особый интерес к задачам Цп вызван тем, что во многих практических задачах необходимо находить целочисленное решение ввиду дискретности ряда искомых переменных. К их числу относятся: задачи оптимизации раскрое, оптимальное проектирование машин и оборудования, оптимизация системы сервиса. Для нахождения оптимального решения целочис задач применяют спец методы, в которых учитывается, что число возможных решений является конечным. Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами целочисленного (дискретного)программирования:
Двойственные опенки как мера влияния ограничений на целевую функцию. Оценка как мере влияния ограничений на ЦФ. Это свойство вытекает из теоремы об оценках
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 или
или  , где t=1,2,…, n Статист методы исследования исходят из предложения возможности представлять уровни временного ряда в виде суммы нескольких компонент, отражающих законом-сть и случайность развития, в частности, в виде суммы четырех компонент
, где t=1,2,…, n Статист методы исследования исходят из предложения возможности представлять уровни временного ряда в виде суммы нескольких компонент, отражающих законом-сть и случайность развития, в частности, в виде суммы четырех компонент 
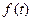 -устойчивая закономерность, наблюдаемая в течение длительного периода времени. Например: а)изменение демографических характеристик популяции, б)рост потребления и т.д. 2. Сезонная компонента -
-устойчивая закономерность, наблюдаемая в течение длительного периода времени. Например: а)изменение демографических характеристик популяции, б)рост потребления и т.д. 2. Сезонная компонента -  связана -это регулярные колебания, которые носят периодический или близкий к нему характер и заканчиваются в течение года. Например: пик продаж товаров для школьников в конце августа – начале сентября. Сезонная компонента со временем может меняться либо иметь плавающий характер. 3. Циклическая компонента
связана -это регулярные колебания, которые носят периодический или близкий к нему характер и заканчиваются в течение года. Например: пик продаж товаров для школьников в конце августа – начале сентября. Сезонная компонента со временем может меняться либо иметь плавающий характер. 3. Циклическая компонента 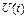 - неслучайная функция, описывающая длительные периоды (более одного года) относительного подъема и спада и состоящая из циклов переменной длительности и амплитуды. Например: Волны Кондратьева, демографические «ямы», спрос и предложение в экономике. 4. Случайная составляющая ряда отражает воздействие многочисленных факторов случайного характера и может иметь разнообразную структуру, начиная от простейшей в виде «белого шума» до весьма сложных, описываемых моделями авторегрессии и скользящего ряда.
- неслучайная функция, описывающая длительные периоды (более одного года) относительного подъема и спада и состоящая из циклов переменной длительности и амплитуды. Например: Волны Кондратьева, демографические «ямы», спрос и предложение в экономике. 4. Случайная составляющая ряда отражает воздействие многочисленных факторов случайного характера и может иметь разнообразную структуру, начиная от простейшей в виде «белого шума» до весьма сложных, описываемых моделями авторегрессии и скользящего ряда. :
:  ,где
,где  Если рассчитанная величина
Если рассчитанная величина 

 , где
, где  - целые j=1,2…p (p<=n). Если р=n то задачу называют полностью целочисленной, если p<n - частично целочисленной.
- целые j=1,2…p (p<=n). Если р=n то задачу называют полностью целочисленной, если p<n - частично целочисленной. . Используя этот метод можно определить не решая задачу заново симплексным методом как изменится значение ЦФ прямой задачи при изменении правых частей ограничений, т.е. можно определить как изменится стоимость выпускаемой продукции при увеличении или уменьшении запасов ресурсов. Данным свойством можно пользоваться только в пределах интервалов устойчивости двойственных оценок. Интервалы устойчивости можно найти в протоколе «устойчивость» поиска решений. Интервалы устойчивости показывают на сколько ед можно увеличить или уменьшить запас ресурсов, чтобы его цена при этом не изменилась. Изменение запасов ресурсов приведет к изменению общей стоимости продукции и к изменению плана выпуска. Однако структура плана при этом не меняется.
. Используя этот метод можно определить не решая задачу заново симплексным методом как изменится значение ЦФ прямой задачи при изменении правых частей ограничений, т.е. можно определить как изменится стоимость выпускаемой продукции при увеличении или уменьшении запасов ресурсов. Данным свойством можно пользоваться только в пределах интервалов устойчивости двойственных оценок. Интервалы устойчивости можно найти в протоколе «устойчивость» поиска решений. Интервалы устойчивости показывают на сколько ед можно увеличить или уменьшить запас ресурсов, чтобы его цена при этом не изменилась. Изменение запасов ресурсов приведет к изменению общей стоимости продукции и к изменению плана выпуска. Однако структура плана при этом не меняется.


