
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальное решение двойственной задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Используя теоремы двойственности можно записать оптимальное решение двойственной задачи, не решая ее отдельно, а используя только решение исходной задачи, найденное симплексным методом. Для этого необходимо установить соответствие между переменными исходной задачи и двойственной. В общем случае:
Пусть при решении исходной задачи получили: Х опт.= (х 1*, х 2*, …, хп+т *), F max + с 1* х 1 + с 2* х 2 +…+ сп+т * хп+т = F *. Для двойственной задачи оптимальное решение будит иметь вид Y опт. = (у 1*, у 2*, …, ут +п*), Z min = Z *+ b 1* y 1 + b 2* y 2 +…+ bт+п * yт+n. При этом выполняются равенства: Z *= F *,
и
Рассмотрим применение этой теоремы на примере задачи об использовании ресурсов. Пример. Найти с помощью теорем двойственности оптимум Z min и оптимальное решение Y опт. двойственной задачи для задачи об использовании ресурсов. Решение. Установим соответствие между переменными исходной и двойственной задач. Решая задачу об использовании ресурсов симплексным методом, мы имели две (п = 2) первоначальные переменные х 1, х 2 и четыре (т = 4) балансовые переменные х 3, х 4, х 5 и х 6. Ранее мы сформулировали двойственную задачу:
при ограничениях и условии неотрицательности Как видим, в двойственной задаче присутствуют четыре (т = 4) первоначальные переменные у 1, у 2, у 3 и у 4. Для преобразования ограничительных неравенств в равенства (при решении двойственной задачи симплексным методом) потребуется ввести две (п = 2) балансовые переменные у 5 и у 6. Тогда соответствие между переменными можно записать так:
На последнем шаге решения исходной задачи симплексным методом, мы получили Х опт.= (6, 4, 0, 0, 1, 3) и F max + 0,8 х 3 + 0,6 х 4 = 24. Для двойственной задачи оптимальное решение будет иметь вид Y опт. = (у 1*, у 2*, у 3*, у 4*, у 5*, у 6*) и Z min = Z * +b 1* y 1 + b 2* y 2 + b 3* y 3 + b 4* y 4 + b 5* y 5 + b 6* y 6.
Используя теорему двойственности, можем записать: Z *= F * = 24,
и
Таким образом, Y опт.= (0,8; 0,6; 0, 0, 0, 0), Z min = 24 +0 · y 1 + 0 · y 2 + 1· y 3 +3· y 4 +6· y 5 + 4· y 6 = 24 + y 3 +3 y 4 +6 y 5 + 4 y 6.
Вывод. Оптимальное решение двойственной задачи будет иметь вид Y опт. = (0,8; 0,6; 0; 0; 0; 0), Z min= 24 + y 3 +3 y 4 +6 y 5 + 4 y 6.
Литература
7. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. Пособие/ под ред. проф. Н.Ш.Кремера. – М.: Высшее образование, 2009 8. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2: Учеб. пособие для вузов / П.Е.Данко, А.Г.Попова, Т.Я.Кожевникова. – 6-е изд. – М.: ООО «Издательство Оникс»: ООО Издательство «Мир и Оразование», 2006 9. Конюховский П.В. Математические методы исследования операций в экономике: Учебное пособие. – СПб.: Питер, 2002
Расчетно-графические задания для студентов очной формы обучения Расчетно-графическое задание № 1 Элементы векторной алгебры, линейной алгебры и аналитической геометрии Задача 1. 1-10. Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку полученного решения.
1.
3.
5.
7.
9. Задача 2. 11-20. Даны векторы
Задача 3.
21-30. Даны вершины А 1(х1, у1, z1), А 2(х2, у2, z2), А 3(х3, у3, z3), 1) длину ребра А 1 А 2; 2) угол между ребрами А 1 А 2 и А 1 А 4; 3) уравнение грани А 1 А 2 А 3 и ее площадь; 4) уравнения высоты, опущенной из вершины А 4 на грань А 1 А 2 А 3.
Задача 4. 31-40. Составить уравнение множества точек, для каждой из которых выполняется следующее условие: 31. Сумма квадратов расстояний до точек А (1,1) и В (-3,3) равна 20. 32. Сумма квадратов расстояний до точек А (3,0), В (0,4) и 33. Сумма квадратов расстояний до точек А (3,-3), В (-1,1), 34. Квадрат расстояния до точки А (0,3) на 3 больше квадрата расстояния до оси абсцисс. 35. Сумма расстояний до точек А (6,0) и О (0,0) равна 10. 36. Квадрат расстояния до точки А (2,0) на 16 больше квадрата расстояния до оси координат. 37. Сумма квадратов расстояний до сторон прямоугольника, образованного прямыми х=0, у=0, х-4=0, у-2=0, равна 20. 38. Расстояние до точки А (0,3) равно расстоянию до оси абсцисс. 39. Разность расстояний до точек А (0,10) и О (0,0) равна 8. 40. Расстояние до точки А (2,0) равно расстоянию до оси ординат.
Расчетно-графическое задание № 2 Дифференциальное исчисление функций одной переменной. Применение дифференциального исчисления для исследования функций и построения их графиков
Задача 1. 41-50. Найти пределы: 41. а) 42. а) 43. а) 44. а) 45. а) 46. а) 47. а) 48. а) 49. а) 50. а) Задача 2. 51-60. Задана функция y=f(x). Найти все точки разрыва функции, если они существуют. Построить график функции.
51.
53.
55.
57.
59. Задача 3. 61-70. Найти производные следующих функций: 61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
Задача 4. 71-80. Вычислить приближенно 71. 76.
Задача 5. 81-90. Заданные функции исследовать методами дифференциального исчисления. На основании результатов исследований построить графики функций. 81.
83.
85.
87.
89.
Расчетно-графическое задание № 3 Неопределенный интеграл Определенный интеграл
Задача 1. 91-100. Найти интегралы. Результаты проверить дифференцированием.
91.
92.
93. 94.
95.
96.
97. 98.
99.
100.
Задача 2. 101-110. Найти площадь фигуры, ограниченной заданными линиями. Сделать рисунок. 101. у=х 3, у= 4 х. 102. у= 4 -х 2, у= 103. у=х 2, 105. 107. у= 3-2 х, у=х 2. 108. у= 2 -х 2, у= х 2. 109. у= Задача 3. 111-120. Вычислить несобственный интеграл или доказать его расходимость. 111. 115. 119.
Расчетно-графическое задание № 4 Функции нескольких переменных. Ряды. Обыкновенные дифференциальные уравнения
Задача 1. 121-130. Задана функция а) наименьшее и наибольшее значение функции б) вектор
121. 122. 123. 124. 125. 126. 127. 128. 129. 130.
Задача 2. 131-140. Исследовать на сходимость данный ряд. 131. 134. 137. 140.
Задача 3. 141-150. Найти область сходимости данного ряда. 141. 145. 149.
Задача 4. 151-160. Найти общее решение дифференциального уравнения. 151. 153. 155. 157. 159. Задача 5. 161-170. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. 161. 162. 163. 164. 165. 166. 167. 168. 169. 170.
Расчетно-графическое задание № 5 Теория вероятностей и математическая статистика Задача 1 1–10. 1. Подбрасываются две игральные кости. Требуется: 1) описать множество элементарных случайных событий, 2) найти вероятности событий А ={выпадение двух «шестерок»}, В = {выпадение хотя бы одной «шестерки»}, С = {выпадение одной «шестерки»}. 2. В контейнере находятся 40 телевизоров, среди которых 5 имеют скрытые дефекты. Найти вероятность того, что 3 наудачу выбранных телевизора не будут иметь дефектов. 3. Аудитор проверяет три счета. Вероятность правильного оформления счета равна 0,9. Найти вероятности событий А = {правильно оформлены три счета}, В = {правильно оформлены два счета}, С = {правильно оформлен один счет}, D = {правильно оформлен хотя бы один счет}. 4. Инвестор наудачу приобретает акции 2-х фондов из 10. Среди 10 фондов 4 невыгодные. Найти вероятности событий А = {инвестор вкладывает деньги в выгодные фонды}, В = {инвестор вкладывает деньги в невыгодные фонды}, С ={инвестор вкладывает деньги хотя бы в один выгодный фонд}. 5. В каждом из двух ящиков содержатся 6 черных и 4 белых шара. Из первого ящика наудачу переложили во второй ящик 1 шар. Найти вероятность того, что два наугад взятые шара из второго ящика будут белыми. 6. На склад поступают однотипные детали с двух заводов – №1 и №2. Завод №1 поставляет 30% деталей, из которых 10% имеют низкое качество. Завод №2 производит детали, из которых 80% имеют высокое качество. Найти вероятность того, что наугад взятая со склада деталь будет высокого качества.
7. Из 3-х урн наудачу извлекается один шар в соответствие с правилом: при подбрасывании игральной кости если выпадает 1 очко, то выбирается урна 1; если выпадает 2, 3 или 4 очка, то выбирается урна 2; если выпадает 5 или 6 очков, то урна 3. В урне 1 находится 10 шаров, из них 2 красных, в урне 2 – 15 шаров, из них 3 красных, в урне 3 – 20 шаров, из них 10 красных. Найти вероятности событий А = {будет извлечен красных шар}, В = {извлеченный красный шар принадлежит урне 1}. 8. В магазине представлена обувь 3-х фабрик: 30% обуви поставила фабрика 1, 25% – фабрика 2, остальную обувь – фабрика 3. Покупатель выбирает обувь наудачу. Процент возврата обуви, изготовленной фабрикой 1 – 3%, фабрикой 2 – 1%, фабрикой 3 – 0,5%. Найти вероятности событий А = {обувь покупателем не будет возвращена}, В = {невозвращенная обувь изготовлена фабрикой 3}. 9. Автомат изготавливает однотипные детали, 5% произведенной продукции оказывается бракованной. Найти вероятность того, что из четырех последовательно изготовленных деталей будут бракованными не более двух. 10. Вероятность поражения стрелком мишени при одном выстреле равна 0,8. Найти вероятность того, что при пяти последовательных выстрелах будет не менее четырех попаданий.
Задача 2 11–16. Задана плотность распределения вероятностей 1) определить коэффициент А; 2) найти функцию распределения 3) схематично построить графики 4) найти математическое ожидание и дисперсию Х; 5) найти вероятность того, что Х примет значение из интервала 11.
13.
15.
17–20. Задана функция распределения 1) найти плотность распределения вероятностей 2) определить коэффициент А; 3) схематично простроить графики 4) найти математическое ожидание и дисперсию Х; 5) найти вероятность того, что Х примет значение из интервала 17.
19.
Задача 3 21–30. Заданы математическое ожидание 1) написать плотность распределения вероятностей 2) найти вероятность того, что Х примет значение из интервала
Задача 4 31–40. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью p. Опыт повторяют в неизменных условиях n раз. 31. 32. 33. 34. 35. 36.
37. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


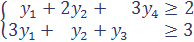
 .
. 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 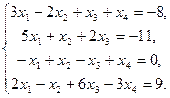
 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы  образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора  в этом базисе. Систему линейных уравнений решить методом Крамера.
в этом базисе. Систему линейных уравнений решить методом Крамера. (7,3,0),
(7,3,0),
 (4,1,1),
(4,1,1),
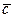 (-7,1,12),
(-7,1,12),
 б)
б) 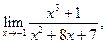 в)
в) 
 б)
б)  в)
в) 
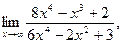 б)
б)  в)
в) 
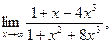 б)
б)  в)
в) 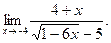
 б)
б) 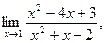 в)
в) 
 б)
б)  в)
в) 
 б)
б) 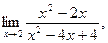 в)
в) 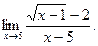
 б)
б)  в)
в) 
 б)
б) 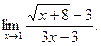
 б)
б)  в)
в) 
 52.
52. 
 54.
54. 
 56.
56. 
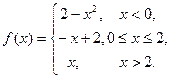 58.
58. 
 60.
60. 
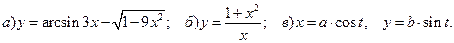



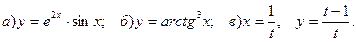





 , заменяя приращение функции ее дифференциалом.
, заменяя приращение функции ее дифференциалом. 72.
72.  73.
73.  74.
74.  75.
75. 
 77.
77.  78.
78. 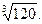 79.
79.  80.
80. 
 82.
82. 
 84.
84. 
 86.
86.  .
. 88.
88. 
 90.
90. 

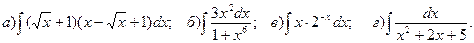


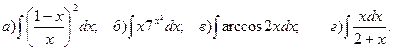





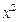 -2 x
-2 x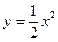 , у= 2 х. 104. у= 2 х 2, у=
, у= 2 х. 104. у= 2 х 2, у=  .
. ,
,  106. у=
106. у=  , у= 4 х 3/2.
, у= 4 х 3/2. ,
,  . 112.
. 112. 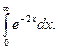 113.
113.  . 114.
. 114.  .
.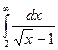 . 116.
. 116.  117.
117.  . 118.
. 118.  .
. . 120
. 120  .
.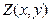 . Найти:
. Найти: – градиент функции
– градиент функции  ; а) Д:
; а) Д:  ; б)
; б)  .
. ; а) Д:
; а) Д:  ; б)
; б) 
 ; а) Д:
; а) Д: 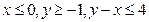 ; б)
; б)  .
. ; а) Д:
; а) Д:  ; б)
; б) 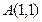 .
.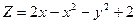 ; а) Д:
; а) Д:  ; б)
; б)  .
. ; а) Д:
; а) Д:  ; б)
; б)  .
.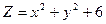 ; а) Д:
; а) Д:  ; б)
; б)  ; а) Д:
; а) Д:  ; б)
; б) 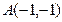 .
. ; а) Д:
; а) Д:  ; б)
; б)  .
. ; а) Д:
; а) Д:  ; б)
; б)  .
.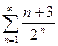 . 132.
. 132.  . 133.
. 133.  .
. . 135.
. 135.  . 136.
. 136. 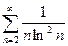 .
. . 138.
. 138.  . 139.
. 139.  .
.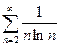 .
. . 142.
. 142.  . 143.
. 143.  . 144.
. 144.  .
. . 146.
. 146.  . 147.
. 147.  . 148.
. 148. 
 . 150.
. 150.  .
. . 152.
. 152. 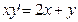 .
. 154.
154.  .
.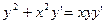 . 156.
. 156.  .
.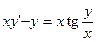 . 158.
. 158.  .
.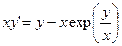 . 160.
. 160.  .
.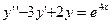 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  .
.  ,
,  ,
,  .
.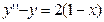 ,
,  .
. ,
, 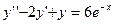 ,
,  ,
, 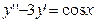 ,
,  ,
, 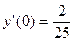 .
. ,
,  .
.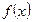 непрерывной случайной величины Х. Требуется:
непрерывной случайной величины Х. Требуется: ;
; .
. 12.
12. 
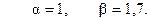
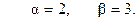
 14.
14. 


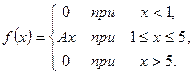 16.
16. 

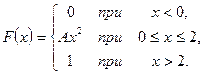 18.
18. 
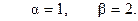

 20.
20. 
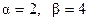 .
. и среднее квадратическое отклонение
и среднее квадратическое отклонение 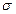 нормально распределенной случайной величины Х. Требуется:
нормально распределенной случайной величины Х. Требуется: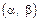 .
. ,
,
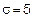 ,
,
 ,
,
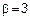 .
.
 ,
,
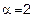 ,
,
 .
.
 ,
,
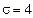 ,
,
 ,
,
 .
.
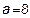 ,
,
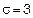 ,
,
 ,
,
 .
.
 ,
,
 ,
,
 ,
,
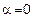 ,
,
 ,
,
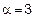 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 ,
,
 . Определить вероятность того, что в 900 опытах событие А произойдет от 250 до 320 раз.
. Определить вероятность того, что в 900 опытах событие А произойдет от 250 до 320 раз. . Определить вероятность того, что относительная частота появления события А отклонится от
. Определить вероятность того, что относительная частота появления события А отклонится от  не более, чем на 0,05.
не более, чем на 0,05. . Определить вероятность того, что в 1000 опытах событие А произойдет не менее чем 580 раз.
. Определить вероятность того, что в 1000 опытах событие А произойдет не менее чем 580 раз. . Определить вероятность того, что в 700 опытах событие А произойдет в меньшинстве опытов.
. Определить вероятность того, что в 700 опытах событие А произойдет в меньшинстве опытов. . Определить вероятность того, что в 900 опытах событие А произойдет в большинстве опытов.
. Определить вероятность того, что в 900 опытах событие А произойдет в большинстве опытов. . Определить вероятность того, что в 800 опытах относительная частота появления события А отклонится от вероятности
. Определить вероятность того, что в 800 опытах относительная частота появления события А отклонится от вероятности  не более, чем на 0,05.
не более, чем на 0,05. . Найти, какое отклонение относительной частоты появления события А от
. Найти, какое отклонение относительной частоты появления события А от 


