
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 2. Размерность и базис. Евклидово пространствоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§3. Размерность и базис векторного пространства Линейная комбинация векторов Тривиальная и нетривиальная линейная комбинация Линейно зависимые и линейно независимые векторы Свойства векторного пространства, связанные с линейной зависимостью векторов п -мерное векторное пространство Размерность векторного пространства Базис Разложение вектора по базису §4. Переход к новому базису Матрица перехода от старого базиса к новому Координаты вектора в новом базисе §5. Евклидово пространство Скалярное произведение Евклидово пространство Длина (норма) вектора Свойства длины вектора Угол между векторами Ортогональные векторы Ортонормированный базис
§ 3. Размерность и базис векторного пространства
Рассмотрим некоторое векторное пространство (V, Å, ∘) над полем Р. Пусть Линейной комбинацией векторов
Если все скаляры Если хотя бы один скаляр отличен от нуля, линейная комбинация называется нетривиальной. Векторы
Векторы
Пример. Рассмотрим множество упорядоченных наборов четверок действительных чисел – это векторное пространство над полем действительных чисел. Задание: выяснить, являются ли векторы Решение. Составим линейную комбинацию этих векторов: В этом равенстве запишем векторы в виде столбцов чисел:
Если найдутся такие числа Выполним действия:
Таким образом, задача сводится к решению системы линейных уравнений:
Решая ее, получим:
Ранги расширенной и основной матриц системы равны Пусть Итак, для данных векторов существует нетривиальная линейная комбинация, например при
Отметим некоторые свойства векторного пространства, связанные с линейной зависимостью векторов: 1. Если векторы 2. Если среди векторов 3. Если часть векторов
Векторное пространство V называется п -мерным векторным пространством, если в нем найдется п линейно независимых векторов, и любой набор из (п + 1) векторов является линейно зависимым. Число п называется размерностью векторного пространства, и обозначается dim(V) от английского «dimension» – размерность (измерение, размер, габарит, величина, протяженность и т.д.). Совокупность п линейно независимых векторов п -мерного векторного пространства называется базисом.
Формула (*) называется разложением вектора В векторном пространстве может быть более одного или даже бесконечно много базисов. В каждом новом базисе один и тот же вектор будет иметь разные координаты.
§ 4. Переход к новому базису
В линейной алгебре часто встает задача нахождения координат вектора в новом базисе, если известны его координаты в старом базисе. Рассмотрим некоторое п -мерное векторное пространство (V, +, ·) над полем Р. Пусть в этом пространстве есть два базиса: старый Задача: найти координаты вектора Пусть векторы нового базиса в старом базисе имеют разложение:
Выпишем координаты векторов
Полученная матрица называется матрицей перехода от старого базиса к новому.
Матрица перехода связывает координаты любого вектора в старом и новом базисе следующим соотношением:
где
Таким образом, задача нахождения координат вектора в новом базисе сводится к решению матричного уравнения:
Итак, координаты вектора
Пример. В некотором базисе
Найти координаты вектора Решение. 1. Выпишем матрицу перехода к новому базису, т.е. координаты векторов
2. Найдем матрицу А –1:
3. Выполним умножение
Ответ:
§ 5. Евклидово пространство
Рассмотрим некоторое п -мерное векторное пространство (V, +, ·) над полем действительных чисел R. Пусть Введем в этом векторном пространстве метрику, т.е. определим способ измерения длин и углов. Для этого определим понятие скалярного произведения. Скалярным произведением двух векторов
где Т.е. мы определили еще одну бинарную операцию: V´V® R. Векторное пространство, в котором задано скалярное произведение, называется евклидовым пространством, если выполняются равенства: 1). 2). 3). 4). Длиной (нормой) вектора в евклидовом пространстве называется квадратный корень из его скалярного квадрата:
Имеют место следующие свойства длины вектора: 1. 2. 3.
Введя понятие длины вектора, можно определить угол между двумя векторами. Угол φ между векторами Два вектора называются ортогональными, если их скалярное произведение равно нулю. Исходя из определения угла между векторами, видно, угол между двумя ненулевыми ортогональными векторами равен 90°. Базис Во всяком п -мерном евклидовом пространстве существует ортонормированный базис.
Аналитическая геометрия
|
||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.152.183 (0.009 с.) |

 – некоторые элементы множества V, т.е. векторы.
– некоторые элементы множества V, т.е. векторы. :
: .
. .
. :
: .
. ,
,  и
и  линейно зависимыми.
линейно зависимыми. , где
, где  – неизвестные числа. Потребуем, чтобы эта линейная комбинация была равна нулевому вектору:
– неизвестные числа. Потребуем, чтобы эта линейная комбинация была равна нулевому вектору: 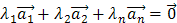 .
.





 и меньше числа неизвестных
и меньше числа неизвестных 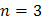 , следовательно, система имеет бесконечное множество решений.
, следовательно, система имеет бесконечное множество решений. , тогда
, тогда  и
и  .
. , которая равна нулевому вектору, значит, эти векторы линейно зависимы.
, которая равна нулевому вектору, значит, эти векторы линейно зависимы. .
. по базису
по базису  , а числа
, а числа  – координатами вектора
– координатами вектора  .
. в новом базисе.
в новом базисе. ,
, в матрицу не строками, как они записаны в системе, а столбцами:
в матрицу не строками, как они записаны в системе, а столбцами:
 ,
, - искомые координаты вектора
- искомые координаты вектора  , где Х – матрица-столбец координат вектора
, где Х – матрица-столбец координат вектора  .
. .
. даны разложения векторов:
даны разложения векторов: ,
,  ,
,  ,
, .
. в базисе
в базисе  .
. в старом базисе запишем столбцами:
в старом базисе запишем столбцами:




 , где
, где  – координаты вектора
– координаты вектора  :
:
 .
. называется число
называется число ,
, – координаты векторов
– координаты векторов  ;
; ;
; ;
; , причем
, причем  .
. .
. ;
; , где α – действительное число;
, где α – действительное число; (неравенство треугольника).
(неравенство треугольника). .
.


