
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проективная прямая. Проективная система координат в евклидовом пространстве.
Опр. Пучком на Евклидовой плоскости называется множество всех прямых, проходящих через некоторую фиксированную точку S. S – центр пучка, пучок обозначается Отображение Расширенная черта – Евклидова прямая, дополненная несобственной точкой
Опр: Мн-во P1 наз. проективной прямой, если существует биективное отображение множества на пучок прямых. Элементы мн-ва Р1 наз. точками проективной прямой. Т1: Пучок прямых на плоскости является проективной прямой. Док-во: Рассмотрим отображение Т2: Расширенная прямая – проективная прямая. Док-во: Рассм. перспективное отображение расширенной прямой на пучок Опр: Пусть дан пучок Опр: Аффинная система координат Т1: Определение проективных координат точки не зависит от выбора направляющего вектора. Т2: Определение проективных координат прямой в пучке не зависит от выбора аффинной системы координат, согласованной с проективной системой координат. Т3: Каковы бы ни были три различные точки Е1 Е2, Е0 проективной прямой, существует единственная система проективных координат, в которой эти точки имеют координаты Е1 (1: 0), Е2(0: 1), Е0(1: 1).
22. Простае алгабраічнае пашырэнне поля. Вызваленне ад алгебраічнай ірацыянальнасці ў назоўніку дробу. Опред. число
Пр. 1 Опред. Неприводимый полином над полем Опред. Степенью миним полинома наз. Степень алгебраич числа Пр.2 Опред. Пусть Опред. Расширение Опред. Избавление от иррац в числителе. Т. □ по опред Значит д-ли, что
Единственность. Полином Допустим, что
23. Простыя лікі. Бясконцасць мноства простых лікаў. Кананічны раскладсастаўнога ліку і яго адзінасць. Определение. Натурал. число p>1 наз. простым, если оно делится только на 1 и себя (др. натур. Делителей нет; др. полож. целых делителей не имеет). Определение. Натур. число наз. составным, если оно имеет делители кроме 1 и себя. 1 не является ни простым, ни составным числом. Теорема Евклида: множество простых чисел бесконечно. Док-во от противного: Пусть мн-во простых чисел конечно, т.е. p1,p2,…,pn. Рассмотрим число p=p1p2….pn+1. По св-ву 1(каждое натур. число n>1 имеет хотя бы 1 простой делитель) число p имеет простой делитель; обозначим его q.
Теорема.: Каждое натуральное число >1 раскладывается в произведение простых чисел. Такое разложение единственное с точностью до порядка следования сомножителей. Док-во:1. Существование. ММИ по n. 1) n=2, 2=2. 2) допустим, что произвольное натуральное число < n раскладывается на простые множители. 3) докажем, что n раскладывается на простые множители. По св-ву (каждое натур. число n>1 имеет хотя бы 1 простой делитель) n имеет хотя бы 1 простой делитель p1 и тогда мы n можем записать n=p1n1, n1<n. Возможны 2 случая: 1) n1=1, n=p1. 2) n1>1, то по предположению следующие n1=p2p3…pk – произведение простых чисел, тогда наши n в этом случае равно n=p1p2p3…pk 2. Единственность ММИ по n. 1)n=2; 2) пусть единственность имеет место для любого натурального числа <n. 3) докажем для n (от противного). Пусть n с одной стороны n=p1p2….pn. Или n=q1q2…qs… Тогда p1p2…pk=q1q2…qs. Левая часть рав-ва делится на p1, значит, и правая часть делится на p1. Следовательно, одни из сомножителей q1,q2,…,qs совпадает с p1. Без ограничения общности можем считать, что p1=q1. Раз p1=q1, сократим на p1. Получим p2…pk=q2….qs. (p2…pk)<n, поэтому по предположению индукции такое представление единственное. Значит k=s и простые числа q2…qs отличаются от простых чисел только порядком следования. Ч.т.д.
Опр.: представление натурального Опр.: каноническим разложением целого числа
24. Рауназначныя сістэмы лінейных раўнанняў. Рашэнне сістэмыліненных раўнанняў метадам паслядоўнага выключення невядомых. Крытэрыі супольнасци сістэмы лінейных раўнанняў.
Опр.Расширение с-мы наз. с-ма чисел Опр. Когда с-ма имеет решения, то она наз. совместной, когда не, то несовместной. Опр. Совместная с-ма наз. определенной, когда имеет только 1 решение, когда больше, то неопределенной. Опр. 2 с-мы наз. эквивалентными, когда мн-ва их решений совпадают (мн-ва м. б. и пустые). Элем. преобразования с-мы: 1) Смена местами уравнений с-мы, 2) умножение 2-х частей уравнения на число Решение системы линейных уравнений методом последовательного выделения неизвестных (м-д Гауса). 1) Выписать расширенн-ю м-цу. 2) С помощью элем-х преобразований строк привести ее к ступенчатого вида. 3) Определить ранг м-цы А и ранг поширен-й м-цы. а) когда они не ровны, то с-ма несовместимая (нет реш.), б) когда ровны, то с-ма совместимая. 4) Найти базисный минор м-цы с-мы; неизвестные, которым соответствуют столбцы базисного минора будут базисными неизвестными, остальные - свободными. (1) (2) Теор. Кронекера-Капэли (критерий совместимости с-мы лин. уравн): система лин-х уравнений имеет решение т. и т. т., когда ранги матрицы коэффицентов и расширенной матрицы с-мы равны. Опр. Ранг матрицы – это кол-во столбцов у МЛНП с-мы столбцов Опр. А =
25. Сістэма аксіём Вейля трохмернай эўклідавай прасторы і яе несупярэчлівасць. При построении аксиоматики Вейля основными объектами являются «точка» и «вектор». Основные отношения аксиоматики Вейля: мн-во точек Е3: А, В, С… мн-во векторов V: a,b,c,d… 1.Сложение векторов Для любой упорядоченной пары векторов ставится в соответствие третий вектор, который обозначается 2.Произведение векторов на действительное число Для любого вектора 3.Соотношение точек и векторов Каждой упорядоченной паре точек ставится в соответствие некоторый вектор, который обозначается 4.Отношение скалярного произведения Упорядоченной паре векторов ставится в соответствие некоторое число, которое обозначается I.Аксиомы векторного пространства: 1) II.Аксиомы размерности: 1) III.Аксиомы соответствия векторов и точек: 1)для любой точки Аϵ Е3 и любого вектора m ϵV существует единственная точка ВϵЕ3 , такая что IV.Аксиомы скалярного произведения: 1) Теорема. Аксиоматика Вейля трехмерного пространства непротиворечива (если непротиворечива арифметика действительных чисел). Док-во: для доказательства построим модель аксиоматики. «Точка» - упорядоченная тройка действительных чисел А=(а1,а2,а3). «Вектор» - столбец из трех действительных чисел b= Покажем это. …(подставить эти значения во все аксиомы).
|
|||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.65 (0.027 с.) |
 .
. называется перспективным отображением прямой d в пучок
называется перспективным отображением прямой d в пучок 
 , которое каждой прямой
, которое каждой прямой  пучка ставит в соответствие эту же прямую. Это тождественное отображение является биективным. По определению пучок – проективная прямая ■
пучка ставит в соответствие эту же прямую. Это тождественное отображение является биективным. По определению пучок – проективная прямая ■ . Так как
. Так как  явл. биективным отображением, то и расширенная прямая (по опр. проективной прямой) является проективной прямой. ■
явл. биективным отображением, то и расширенная прямая (по опр. проективной прямой) является проективной прямой. ■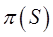 . Проективной прямой в пучке назыв. упорядоченная тройка прямых
. Проективной прямой в пучке назыв. упорядоченная тройка прямых  .
. назыв. согласованной с проективной системой координат, если
назыв. согласованной с проективной системой координат, если  - направляющие вектора прямых
- направляющие вектора прямых  соответственно и выполняется условие
соответственно и выполняется условие  . Пусть SM – произвольная прямая пучка. Проективными координатами прямой SM в проективной системе координат – R наз. класс упорядоченных пар чисел, пропорциональных паре
. Пусть SM – произвольная прямая пучка. Проективными координатами прямой SM в проективной системе координат – R наз. класс упорядоченных пар чисел, пропорциональных паре  , где
, где  - координаты направляющего вектора
- координаты направляющего вектора  прямой SM в согласованной аффинной системе координат.
прямой SM в согласованной аффинной системе координат.  . Пишут:
. Пишут: 
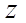 , кот явл корнем нек-го полинома над полем
, кот явл корнем нек-го полинома над полем  наз. Алгебраичным над этим полем, по-другому трансциндентный над
наз. Алгебраичным над этим полем, по-другому трансциндентный над  – алгебр. число, т.к явл корнем полинома
– алгебр. число, т.к явл корнем полинома  .
. со старшим коэф-том =1(унитарный), корнем кот явл число
со старшим коэф-том =1(унитарный), корнем кот явл число 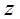 наз. Миним полиномом числа.
наз. Миним полиномом числа.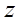 .
.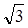 явл корнем полинома
явл корнем полинома  (непривод полином миним).
(непривод полином миним). – поле,
– поле, 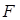 – его подполе
– его подполе  . Поле
. Поле  . Пусть
. Пусть  – некоторое число, обоз
– некоторое число, обоз  .
. поля
поля 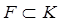 ,
,  Î
Î  назыв. простым алгебр. расширением.
назыв. простым алгебр. расширением. .
.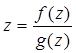 , где
, где  и
и  – полиномы над полем
– полиномы над полем  ,
,  (
( – алг. число).
– алг. число). 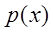 – миним полином алгебраич числа
– миним полином алгебраич числа  ,
,  Î
Î  )
)  - мин. Полином алг. числа
- мин. Полином алг. числа  . Тода
. Тода  и
и  – взаимнопростые полиномы Þ $ u(х), v(х) Î
– взаимнопростые полиномы Þ $ u(х), v(х) Î 
 . Д-жем, что и
. Д-жем, что и  .
.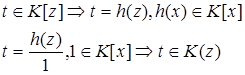
 с этими св-вами ед.
с этими св-вами ед. еще 1 полином
еще 1 полином  степени
степени  такой,что
такой,что  . Рассм полином
. Рассм полином 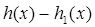 . Когда
. Когда  , то это полином степени
, то это полином степени  , корнем кот явл число
, корнем кот явл число  . ■
. ■ . Ч.т.д.
. Ч.т.д. в виде
в виде 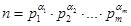 , где
, где 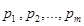 разные простые числа,
разные простые числа,  называется каноническим представлением (каноническим разложения числа
называется каноническим представлением (каноническим разложения числа  ).
). на простые множители называется представление числа
на простые множители называется представление числа  в виде
в виде  .
. (1)
(1)  – поле.
– поле. – м-ца системы,
– м-ца системы,  – расшир-ая м-ца с-мы.
– расшир-ая м-ца с-мы. когда при подстановке все равенства выполняются.
когда при подстановке все равенства выполняются.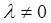 , 3) добавление к одному уравнению с-мы 2-го уравнения, умноженного на число.
, 3) добавление к одному уравнению с-мы 2-го уравнения, умноженного на число. , то все неизвечные – базисные и с-ма имеет ед. решение (м. найти с пощ. ф-л Крамера:
, то все неизвечные – базисные и с-ма имеет ед. решение (м. найти с пощ. ф-л Крамера:  ).
). , то с-ма имеет бесконечно много реш. Для их нахождения с-му записываем т. образ., чтоб в левой часте каждого ур. остальсь только базисные неизвестные. Далее базисные неиз-ыя м. выявить через свободные, напр., с помщ. ф-л Крамера, т. обр. получится общее реш. исходной с-мы. Частное реш. м. получить, когда придать свободным неизвестным конкретные числовые значения
, то с-ма имеет бесконечно много реш. Для их нахождения с-му записываем т. образ., чтоб в левой часте каждого ур. остальсь только базисные неизвестные. Далее базисные неиз-ыя м. выявить через свободные, напр., с помщ. ф-л Крамера, т. обр. получится общее реш. исходной с-мы. Частное реш. м. получить, когда придать свободным неизвестным конкретные числовые значения
 , k
, k  min{m,n}. Выделим в А k рядов и k столбцов. Эл-ты матрицы А, которые стат на пересечении этих k рядов і k столбцов, образуют матриц размерности
min{m,n}. Выделим в А k рядов и k столбцов. Эл-ты матрицы А, которые стат на пересечении этих k рядов і k столбцов, образуют матриц размерности  , дэтерминант которой наз. минором k-го порядка матрицы А.
, дэтерминант которой наз. минором k-го порядка матрицы А. +
+  ϵV
ϵV и действительного числа αставится в соответствие вектор, который обозначается α
и действительного числа αставится в соответствие вектор, который обозначается α  ϵV
ϵV и называется скалярным произведением.
и называется скалярным произведением. 2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7) 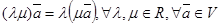 8)
8) 
 2)
2) 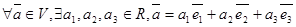
 =
= 
 2)для любых векторов а,в,с
2)для любых векторов а,в,с  +
+  =
= 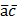 +
+ 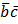 3) αϵR, (α
3) αϵR, (α  ) 4)
) 4)  >0
>0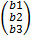 .сумма векторов а=
.сумма векторов а=  и b=
и b=  . Произведение вектора а=
. Произведение вектора а= 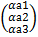 . Паре точек А=(а1,а2,а3) и B=(b1,b2,b3) соответствует вектор
. Паре точек А=(а1,а2,а3) и B=(b1,b2,b3) соответствует вектор  . Скалярным произведением векторов а и b назовем число
. Скалярным произведением векторов а и b назовем число  =а1b1+a2b2+a3b3. Можно показать, что выполняются все аксиомы аксиоматики Вейля.
=а1b1+a2b2+a3b3. Можно показать, что выполняются все аксиомы аксиоматики Вейля.


