
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відарысы прасторавых фігур у паралельнай праекцыі
Опр.: Пусть в пространстве дана плоскость Замечание: Параллельное проектирование зависит от выбора плоскости проекций и проектирующей прямой. Пусть F – проектирующее пространство, тогда Опр.: Изображение фигуры F называется любая фигура, подобная проекции фигуры F на некоторую плоскость. Теорема Польке-Шварца: За изображение произвольной треугольной пирамиды можно принять любой 4-угольник с его диагоналями. Изображением параллелепипеда (в том числе прямоугольного параллелепипеда, куба) является фигура, состоящая из трех пар параллелограммов, причем в каждой паре один получается из другого параллельным переносом. Изображением
Для построения изображения данной пирамиды следует учесть, что по теореме Польке — Шварца за изображение вершины пирамиды и трех вершин основания можно взять вершины произвольного четырехугольника плоскости 0. Тогда изображения остальных вершин основания и всех ребер получаются построением с учетом правил изображений плоских многоугольников.
Шар. При параллельном проектировании шара всегда рассматривается случай, когда это проектирование прямоугольное. При этом контур шара получается в виде окружности. Ось шара - это диаметр шара плоскости сечения.
5. Гладкія паверхні ў трохмернай эўклідавай прасторы. Першая квадратычная форма паверхні. Опред. Пусть G={(u,v)|-1<u<1, -1<v<1}?R-любое мн-во, гомоморфное открытому кругу. Опред. Элем. пов-тью в трехмерном Евклидовом пр-ве назыв. Любое мн-во F гомоморфное открытому кругу. Опред. Пусть F-некоторая элем пов-ть в Е3. Тогда существует гомоморфизм φ, кот отображает открытый круг на мно-во F. (u,v)¾>(φ) φ(u,v)?F Каждой паре чисел (u,v) поставили в соответствие вектор r(u,v) (u,v)¾> вектор r (u,v) Т.о. возникает вектор-ф-ция вектор r= вектор r (u,v), (u,v)?G, кот назыв вектор-ф-цией элем пов-ти или параметризацией элем пов-ти Опред. Поверхностью в трехмерном Евклидовом пр-ве назыв.мн-во, кот можно представить как объединение конечного или счетного мн-ва элем пов-тей. Примером пов-ти, кот не явл элементарными:сфера (сферу можно представить как объединение двух элементарных поверхностей, каждая из которых представляет собой сферу с выколотой точкой), эллипсоид, цилиндр (эллиптический) Опред. Пусть вектор r=вектор (u,v), (u,v)?G-параметризация элем пов-ти. Элем пов-ть наз гладкой класса Ск, если вектор-ф-ция r(u,v)имеет непрерывные части произв до к порядка включительно, кроме того вектор ru не параллелен вектору rv.
Опред. Пусть дана F-гладкая пов-ть, вектор r=вектор (u,v) -ее векторное ур-ние. Первая квадратичная форма пов-ти Найдем скалярный квадрат вектора ( Обозначим E(u,v)= F(u,v)= G= Тогда получим ( Квадратичная форма стоящая в правой части равенства (*) наз первой квадратичной формой пов-ти. E,G,F-коэффициенты 1КФП Поскольку du,dv одновременно не обращаются ноль, то 1КФП явл положительно определяемой. Зная 1КФП можно решать след задачи: 1) Находить длину дуги линии пов-ти 2) Угол м.д линиями на пов-ти 3) Площадь замкнутой обл пов-ти
6.Група афінных пераўтварэнняў плоскасці і некаторыя яе падгрупы Опр. Любое преобразование плоскости называется аффинным преобразованием, если оно любые три точки, принадлежащие одной прямой, отображает в три точки, принадлежащие одной прямой и сохраняет простое отношение трех точек.
Из свойств движения, гомотетии, подобия следует, что эти преобразования плоскости являются частными случаями аффинных преобразований. Лемма. Пусть f1, f2 – аффинные преобразования плоскости, А,В – произвольные точки на плоскости. A’=f1(A), A’=f2(A), B’=f1(B), B’=f2(B). Тогда для любой точки М принадлежащей АВ f1(М)= f2(М). Свойство. Если аффинные преобразования f1, f2 одинаковым образом действуют на А и В, то они одинаковым образом действуют на каждую точку прямой АВ. Док-во. (от противного) М – произвольная точка. f1(М)= М’, f2(М)= М’’. покажем, что М’= М’’. f1, f2 - аффинные преобразования. (АВ,М)=(A’B’,M’), (АВ,М)=(A’B’,M’’), значит, (A’B’,M’)=(A’B’,M’’), тогда М’= М’’. доказано. Теорема. Пусть на плоскости даны две аффинные СК R=(O, М’=f(M), f – аффинное преобразование. Теорема 2. Множество всех аффинных преобразований плоскости образуют подгруппу группы преобразований плоскости. Док-во. Необходимо доказать, что композиция двух аффинных преобразований является аффинным преобразованием и обратное к аффинному преобразованию является аффинным преобразованием. 1)Пусть f1, f2 – аффинные преобразования, тогда f1ᵒ f2 – аффинное преобразование сохраняет принадлежность трех точек одной прямой и простое отношение этих точек, т.к. каждое преобразование f1, f2 обладают такими свойствами. 2)Пусть f – аффинное преобразование, тогда f-1 также является аффинным. Покажем это. А,В,С принадлежат одной прямой. Пусть A’= f-1(A), В’= f-1(В), С’= f-1(С) – отображение (образы). Точки A’,B’,C’принадлежат одной прямой. Если бы это было не так, тогда аффинное преобразование f эти три точки отобразила бы в три точки, не лежащие на одной прямой (противоречие свойству после леммы). Значит, f-1сохраняет простое отношение, так как сохраняет его отображение f, т.к. оно аффинное. Доказано. Опр. Две фигуры F1 и F2 называются аффинно-эквивалентными, если существует аффинное преобразование плоскости f такое, что F2=f(F1). Из Т2 следует, что существует единственное аффинное преобразование, которое любой треугольник отображает на заданный треугольник, любые два треугольника являются аффинно эквивалентными. Теорема. Для того чтобы два треугольника были аффинно эквивалентными, необходимо их обозначить так, чтобы выполнялось условие (AC,F)=(A’C’,F’) и (BD,F)=(B’D’,F’), где F=FCᴖBD, F’=A’C’ᴖB’D’.
7. Гладкія крывыя ў трохмернай эўклідавай прасторы. Формулы Фрэнэ Опр. Элементарной линией наз мн-во Ϫ включ в En(n=2,3…), для кот сущ некоторое гомоморфное отображение числового интервала на мн-во. Или это образ открытого интервала при некотором гомоморфизме. Опр. Пусть Ϫ – элементарная линия и r=r(t)=x(t) Опр. линия наз гладкой класса Ск, если ее можно представить в виде объединения конечного или счетного множества элементарных гладких класса Ск линий.
Среди гладких элементарных линий выделяют бирегулярные ( r’(t)-направляющий вектор. Опр. Пусть Ϫ – гладкая элементарная регулярная линия, r=r(s) ее параметризация. Параметризация линии наз натуральной, если выполняется условие | Теорема. Для любой регулярной линии существует натуральная параметризация.
Формулы Френе Найдём разложение векторов
Продифференцируем равенство (2):
Так как вектор
Теперь из (1) и (4) следует (3). Т.е. получаем k∙ α=-k т.о. получили,
8. Група пераўтварэнняў падобнасці плоскасці і некаторыя яе падгрупы Опр. Преобразование плоскости наз преобразованием гомотетии, если каждой точке М ставится в соответствие точка M’так, что выполняется условие: OM’=kOM, а точке О ставится в соответствие саму эту точку, где О – фиксированная точка плоскости и называется центром гомотетии, k – коэффициент гомотетии. Обозначение: Опр. Преобразование плоскости наз преобразованием подобия, если для любых двух точек А,В и их образов A’, B’ при этом преобразовании выполняется условие A’B’=kАВ, k>0. k - коэффициент подобия. Обозначение: Pk Теорема. Множество всех преобразований подобия образуют подгруппу группы преобразований плоскости. Док-во. 1)Пусть Рк1, Рк2 – два преобразования подобия с коэффициентами к1 и к2. Надо доказать, что Рк1 ᵒ Рк2 – преобразования подобия. Для любых А, В Рк1(А)=A’, Рк2(A’)=A’’. Рк1(B)=B’, Рк2(B’)=B’’. Рк2 ᵒ Рк1(A)=A’’ Рк2 ᵒ Рк1(B)=B’’ Т.к. Рк1 и Рк2 – подобия и A’B’=k1АВ и A’’B’’=k2А’В’, значит, A’’B’’= k1k2АВ, значит, Рк1 ᵒ Рк2 – преобразование подобия с коэффициентом k1k2. 2)Пусть Рк – преобразование подобия с коэффициентом k. Докажем, что Для любых А и В A’=Рк (А) и В’=Рк(В) получаем Теорема. Любое преобразование подобия Рк можно представить в виде композиции ᵩº
Свойства. 1)прямую отображает на прямую, луч на луч, отрезок на отрезок, полуплоскость на полуплоскость, угол на равный ему угол. 2)при преобразовании подобия сохраняется простое отношение трех точек. Замечание. Всякая гомотетия является преобразованием подобия с коэффициентом модуль к. Отсюда следует, что множество всех гомотетий с общим центром образуют подгруппу группы преобразований подобия. Всякое движение является преобразованием подобия с коэффициентом к=1. Множество всех движений плоскости образуют подгруппу преобразований подобия плоскости.
9. Група рухаў плоскасці. Класіфікацыя рухаў Движением пл-ти наз преобразование пл-ти, кот сохраняет расстояние между каждыми 2 точками пл-ти (преобразование пл-ти – биективное отображение пл-ти на себя). Т. Множество всех движений пл-ти образуют подгруппу группы преобразований пл-ти. Док-во. Для доказательства необходимо доказать, что 1)для любых движений f и g композиция fᵒg явл движением, 2)если f движение, то f-1 тоже движение. 1)пусть f и g – движения, А,В – произвольные точки Е2. Обозначим (gᵒf)(A)=A’’, (gᵒf)(B)=B’’. Покажем, что АВ= A’’ B’’. Пусть f(A)=A’, g(A’)=A’’, f(B)=B’, g(B’)=B’’. т.к. f- движение, то A’B’=AB, и g-движение, то A’B’=A’’B’’. Значит, A’’ B’’. Композиция сохраняет расстояние между двумя любыми точками. 2)пусть f- движение. Докажем, что f-1 тоже движение. Возьмем произвольные точки С, D. f-1 (С)=А, f-1 (D)=B, f(A)=C, f(B)=D. Покажем, что CD=AB. Т.к. f- движение, то AB=CD, отсюда следует, что f-1 - движение. Доказано. Свойства движения: 1.Любое движение плоскости 3 точки, принадлежащие одной прямой, отображает в 3 точки, принадлежащие другой прямой. 2.Всякое движение три точки, не принадлежащие одной прямой, отображает в три точки, не принадлежащие одной прямой. 3.Любое движение плоскости прямую отображает на прямую. 4.Любое движение отрезок отображает на равный ему отрезок. 5.Любое движение плоскости треугольник отображает на равный ему треугольник. 6.Любое движение отображает угол на равный ему угол, луч на луч, полуплоскость на полуплоскость и сохраняет простое отношение трех точек. Опр. Пусть фи – движение, R=(o,i,j) – прямоугольная СК, R’=(o’,I’,j’)- образ прямоугольной СК при движении фи. Движение фи называется движением первого рода, если базисы (I,j)и (I’,j’) одинаково ориентированы и фи называется движением второго рода, если эти базисы противоположно ориентированы. Т3.. Пусть фи – движение, которое определяется двумя СК R=(o,i,j) и R’=(o’,I’,j’).), R’= ᵩ(R). Тогда координаты точки М и точки M’ связаны соотношениями
Где ε=±1. Причем, ε=1, если формулы определяют движение первого рода, ε=-1, если формулы определяют движение второго рода. Классификация движений. 1)Всякое движение первого рода является либо тождественным преобразованием, либо параллельным переносом, либо поворотом. 2)Всякое движение второго рода есть осевая или скользящая симметрия.
Определения. 1)Пусть 2)пусть α – некоторый ориентированный угол, О – фиксированная точка на пл-ти. Поворотом пл-ти вокруг точки О наз преобразование пл-ти, при кот каждой т.М, не совпадающей с т.О, ставится в соответствие т.M’ так что: 1.ОМ=OM’. 2.угол MOM’= α,А точке О ставят в соответствие саму эту точку. О – центр поворота. 3)Пусть О – фиксированная т.на пл-ти. Центральной симметрией с центром в т.О наз преобразование пл-ти, кот любой т.М≠0 ставит в соответствие т.M’, симметричную М относительно т.О, а т.О ставит в соответствие саму эту точку. О – центр симметрии. 4)Пусть на пл-ти дана некоторая прямая L. Осевой симметрией относительно пр.L наз преобразование пл-ти, при кот. каждой т.М, не ϵ прям L, ставится в соответствие т.M’, симметрич т.М относит прям L. И кажд т.Р, ϵ прям L, став в соответствие сама эта точка. 5)Пусть L-некоторая прям Е2,
10. Ізамарфізм вектарных прастораў. Бaзіс і памернасць канечнамернай вектарнай прасторы. Падпрасторы Опр. Пусть Р- поле. Непустое мн-ва V наз. линейным пространством (или векторным пространством) над Р (элементы V будем называть векторами, элементы Р- скалярами), когда: 0) На V задана бинарная алгебраическая операция, кот наз. сложением или суммой, это зн., что Опр. Пусть V, U – линейное пр-во над полем P. Отображение Опр. V, U – лин пр-ва над P. Опр. сист вект-в лин. простр V над P Опр. Упорядоченная n-ка Опр. Число вект-в в базисе наз. ее размерностью простр V над P. Обоз. n= Св-ва: 1) если dim V =n, то каждая лин незавмс сист вект-в из V содержит не больше чем n вект-ов. 2) любая миним (па кол-ву вект-ов) полная сист вект-ов образует базис. 3) любая максим лин незав сист вект-ов образует базис. 4) любую лин незав сист вект-в м дополн до базиса. 5) люб конечная сист вект-в, котор владеет св-ом полноты, содержит базис. 6) пусть (1) – базис прастр V. Каждый в-р Опр. Упорядоченная n-ка Опр пусть V лин. простр. над полем Р. Непустое подмн-во U Критерий подпростр. V лин простр над Р. Падмн-во U
11. Кольца. Прыклады кольцаў. Найпрасцейшыя уласцівасці кольца.Падкольца. Гомамарфізмы і ізамарфізмы кольцаў. Непустое множество А – кольцо, если на нем задана бинарная операция, обычно обозначаемая «+» и называемая сложением. Такая, что «К;+» - аддитивная коммутативная группа. И выполняются условия: 1) На К задана бинарная операция обозначаемая «*» и называемая умножением, такая что «К;*»-полугруппа,т.е. 1) Операция сложения и умножения в К согласованы условиями дистрибутивности т.е.
Кольцо К – коммутативно если операция умножения коммутативна т.е. Кольцо К – кольцо с единицей если в нем Прим: «Z;+;*» - комуттативное кольцо с 1 «5Z;+;◦» - коммуттативное кольцо без 1 «С;+; ◦» - кольцо Подкольца Пусть «К;+;◦»-кольцо. Непустое подмножество К в К –подкольцо в К, если оно само является кольцом относительно операций в К. Критерий подкольца: «К;+;◦» - кольцо; К1 Примеры: 5Z- подкальцо в Z К= Mat(nxn;R) K1 = Гомоморфизм и изоморфизм Пусть <K1;+;
-- изоморфизмом, если f - биекция. - биективным (или биекцией, или взаимно однозначным отображением множества E на F), если оно инъективно и сюръективно, или если
12. Кольца цэлых лікаў. Тэарэма аб дзяленні з астачай.
 , рассмотрим на нем бинарное отношение , рассмотрим на нем бинарное отношение  , такое что , такое что 
 относительно отношения эквивалентности относительно отношения эквивалентности  . Мн-во всех классов эквивал – мн-во целых чисел, обозн . Мн-во всех классов эквивал – мн-во целых чисел, обозн  . Класс эквивал пары . Класс эквивал пары  обозн обозн  , целые числа гречискими бквами , целые числа гречискими бквами 
Опр .Сложение целых чисел: Опр .Умножение целых чисел: Опр .Кольцо Т. 1 (преобразование кольца в линейно-упорядоченное кольцо) Пусть Т. 2 Кольцо Определение 2.1. Пусть В этом случае число q называется частным, число r – остатком от деления a на b.
Теорема 2.2. (о делении с остатком) Пусть Док-во: “ Очевидно, что существует q (((b=3: ab: …, -12, -9, -6, -3, 0, 3, 6, … a=10 между 9 и 12))) Тогда рассмотрим a=bq+(-bq+a) и 0≤a-bq<b a=bq+r, 0≤r<b
“ bq+r= b (b(q- 13. Найбольшы агульны дзельнік і найменшы агульны кратны двух лікаў. Опр.: Пусть Опр.: Пусть Лемма: Если Алгоритм Евклида Пусть ТЕОРЕМА ЕВКЛИДА: Последний не равный нулю остаток в алгоритме Евклида равен u Докажем, что Наименьшее общее кратное Опр.: Пусть Опр.: Св-во: Если
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 283; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.241.82 (0.169 с.) |
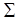 и прямая
и прямая 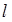 , пересекающая эту плоскость. ПАРАЛЛЕЛЬНЫМ ПРОЕКТИРОВАНИЕМ на плоскость
, пересекающая эту плоскость. ПАРАЛЛЕЛЬНЫМ ПРОЕКТИРОВАНИЕМ на плоскость 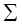 называется такое отображение, при котором каждой точке
называется такое отображение, при котором каждой точке 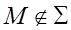 ставится в соответствие точка
ставится в соответствие точка 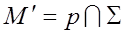 , где
, где 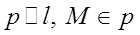 , а каждой точке
, а каждой точке 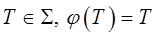 . Плоскость
. Плоскость 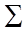 называется плоскостью проекций,
называется плоскостью проекций,  - проектирующей прямой.
- проектирующей прямой.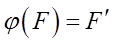 называется ПРОЕКЦИЕЙ на плоскость
называется ПРОЕКЦИЕЙ на плоскость 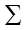 .
.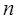 -угольной призмы на плоскости
-угольной призмы на плоскости 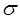 является фигура, состоящая из двух равных
является фигура, состоящая из двух равных 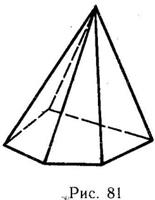 Изображением пирамиды является фигура, состоящая из многоугольника, изображающего основание пирамиды-оригинала, и нескольких треугольников с общей вершиной, изображающих боковые грани пирамиды (рис. 81).
Изображением пирамиды является фигура, состоящая из многоугольника, изображающего основание пирамиды-оригинала, и нескольких треугольников с общей вершиной, изображающих боковые грани пирамиды (рис. 81).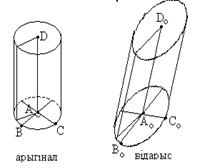 Цилиндр. А0В0, А0С0 - сопряженные диаметры элипса.По Т. Польке-Шварца А0В0С0D0 есть изображение тетраэдра ABCD в некоторой паралл-ой проекции.
Цилиндр. А0В0, А0С0 - сопряженные диаметры элипса.По Т. Польке-Шварца А0В0С0D0 есть изображение тетраэдра ABCD в некоторой паралл-ой проекции.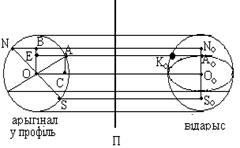 При этом, изображением нижнего основания оригинала будет некий эллипс со сполученными диаматрами А0В0, А0С0. Так как эллипс однозначно определяется своими спал-ми диам-ми, то это изображение совпадает с основным изображением.
При этом, изображением нижнего основания оригинала будет некий эллипс со сполученными диаматрами А0В0, А0С0. Так как эллипс однозначно определяется своими спал-ми диам-ми, то это изображение совпадает с основным изображением.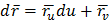 -дифференциал вектор-ф-ции.
-дифференциал вектор-ф-ции.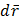
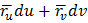 )2=
)2= 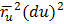 +2
+2 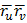 +
+ 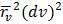
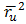
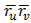
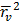
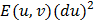 +2F(u,v)dudv+
+2F(u,v)dudv+ 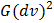 (*)
(*)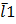 =
=  ,
, 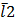 =
= 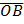 ) и R’=(O’,
) и R’=(O’, 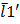 =
= 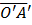 ,
, 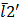 =
=  ). Тогда существует единственное преобразование плоскости, когда систему R отображают в систему R’, причем образ точки М(х,у)R имеет такие же координаты М’(х,у)R’
). Тогда существует единственное преобразование плоскости, когда систему R отображают в систему R’, причем образ точки М(х,у)R имеет такие же координаты М’(х,у)R’ 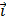 + y(t)
+ y(t) 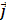 + z(t)
+ z(t) 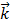 ее параметризация (или вектор-функция). Элементарная линия наз гладкой класса Ск, если функции x(t), y(t), z(t) имеют непрерывные производные до к-го порядка включительно.
ее параметризация (или вектор-функция). Элементарная линия наз гладкой класса Ск, если функции x(t), y(t), z(t) имеют непрерывные производные до к-го порядка включительно.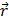 ‘(t0)не параллельно
‘(t0)не параллельно 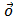 ).
).
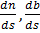 по векторам репера Френе.
по векторам репера Френе. (1), где к – кривизна линии.
(1), где к – кривизна линии.  ┴
┴ 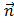 , значит.
, значит. 
 ┴
┴ 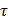 и n, значит, его можно разложить по векторам
и n, значит, его можно разложить по векторам  +æ
+æ  (4) æ-каппа
(4) æ-каппа ∙
∙  (α
(α  æ
æ 
 =-
=- 
 =-
=-  (*) Формулы (*) назыв формулами Френе.
(*) Формулы (*) назыв формулами Френе.
 - тоже преобразование подобия. Покажем это
- тоже преобразование подобия. Покажем это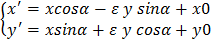
 – некотор. вектор на пл-ти. Преобразование пл-ти, кот. т.М ставит в соответствие такую т. М’, что вектор ММ’=
– некотор. вектор на пл-ти. Преобразование пл-ти, кот. т.М ставит в соответствие такую т. М’, что вектор ММ’=  наз параллельным переносом пл-ти на вектор
наз параллельным переносом пл-ти на вектор 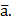
 указан вектор
указан вектор  ), кот удовлетворяет условиям: 1)
), кот удовлетворяет условиям: 1) 
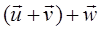 =
=  ; 2)
; 2) 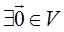 , что
, что 
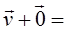
 ; 3)
; 3) 
 такой, что
такой, что 
 ; 4)
; 4)  ;
;  Задана операция умножения скаляров (эл-тов с Р) на векторы (эл-ты из V) (это.зн., что
Задана операция умножения скаляров (эл-тов с Р) на векторы (эл-ты из V) (это.зн., что  ,
,  указан вектор
указан вектор 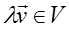 ); 5)
); 5) 
 ; 6)
; 6)  ; 7)
; 7) 

 ; 8)
; 8) 
 наз. линейным (гомоморфизмом лин. пространства), когда 1)
наз. линейным (гомоморфизмом лин. пространства), когда 1) 
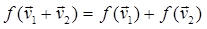 ; 2)
; 2) 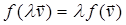
 (1) наз. базисом простр V, если вып. 2усл: 1) сист(1)лин.незав. 2) (усл полноты)
(1) наз. базисом простр V, если вып. 2усл: 1) сист(1)лин.незав. 2) (усл полноты) 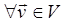



 из разложения
из разложения  в базисе
в базисе  .
. Î V единств образом расклад па базису,это зн
Î V единств образом расклад па базису,это зн  V назыв. подпростр. простр. V, если U явл лінейным прастр. относит опер, котор поредеоены в V. ( наприм Рn[x]
V назыв. подпростр. простр. V, если U явл лінейным прастр. относит опер, котор поредеоены в V. ( наприм Рn[x] 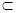 Pn+1[x]
Pn+1[x]  P[x] і каждое из подмн. Явл подпространством)
P[x] і каждое из подмн. Явл подпространством)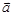 і
і 
 U
U 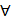 а, в а+в
а, в а+в 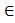 К, 2)
К, 2) 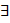 0
0  К,
К,  а,в а+в=в+а, 5)
а,в а+в=в+а, 5)  К1 – подкольцо в К ó 1) К1- аддитивная подгруппа в К; 2)
К1 – подкольцо в К ó 1) К1- аддитивная подгруппа в К; 2) 
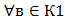 а*в
а*в 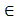 К1
К1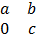 где a,b,c
где a,b,c  > и <K1;
> и <K1; 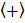 ;
;  > -кольца. Отображение f:K1
> -кольца. Отображение f:K1 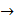 K2 наз. гомоморфизмом колец, если оно сохраняет операцию, т.е.
K2 наз. гомоморфизмом колец, если оно сохраняет операцию, т.е. 
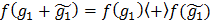

 уравнение f (x) = y имеет одно и только одно решение.)
уравнение f (x) = y имеет одно и только одно решение.) - целое число
- целое число  .
.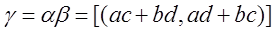
 наз. линейно-упорядоченным, когдана им можно задать такой порядок, что: 1)
наз. линейно-упорядоченным, когдана им можно задать такой порядок, что: 1)  , 2)
, 2) 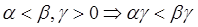 .
. 1)
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  .
.  .
. явл. линейно-упорядоченным.
явл. линейно-упорядоченным. и b≠0. Делением a на b с остатком называется представление числа a в виде a=bq+r, где q, r
и b≠0. Делением a на b с остатком называется представление числа a в виде a=bq+r, где q, r  , 0≤r<ΙbΙ
, 0≤r<ΙbΙ 0≤r<b
0≤r<b ”: рассмотрим все возможные произведения вида bn, n
”: рассмотрим все возможные произведения вида bn, n  : …, -kb, …, -b, 0, b, 2b, 3b, …, kb, …
: …, -kb, …, -b, 0, b, 2b, 3b, …, kb, … ”: пусть
”: пусть  , тогда a=b
, тогда a=b  +
+  , 0≤
, 0≤  => (
=> ( b; т. к. 0≤r,
b; т. к. 0≤r, 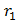 <b, то Ιr-
<b, то Ιr-  b => либо a=0, либо ΙaΙ ≥ΙbΙ)
b => либо a=0, либо ΙaΙ ≥ΙbΙ)  => r=
=> r= 
 . Целое число
. Целое число  называется общим делителем
называется общим делителем  , если
, если 
 , которое является общим делителем
, которое является общим делителем 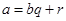 (не обязательно деление с остатком), то 1)
(не обязательно деление с остатком), то 1)  2)
2)  .
. , тогда
, тогда 
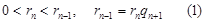 остаток равен нулю. Остатки от делений – это целые неотрицательные числа, которые удовлетворяют условию:
остаток равен нулю. Остатки от делений – это целые неотрицательные числа, которые удовлетворяют условию:  . Эта последовательность не может быть бесконечной. Значит, на каком-то шаге деления получится остаток =0. Этим и объясняется последнее равенство (1). Равенство (1) – алгоритм Евклида.
. Эта последовательность не может быть бесконечной. Значит, на каком-то шаге деления получится остаток =0. Этим и объясняется последнее равенство (1). Равенство (1) – алгоритм Евклида.
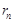 - общий делитель
- общий делитель 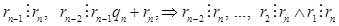 , но тогда
, но тогда 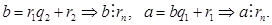 Пусть
Пусть 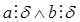 , докажем, что
, докажем, что 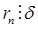 . По алгоритму Евклида сверху вниз
. По алгоритму Евклида сверху вниз 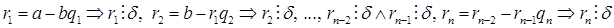 ¢
¢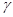 называют из общим кратным, если
называют из общим кратным, если 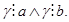
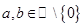 . Натуральное число
. Натуральное число 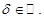
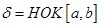 .
.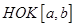 существует, то оно единственное.
существует, то оно единственное.


