
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между сист. акс. Вейля и Гильберта. ⇐ ПредыдущаяСтр 4 из 4
С помощью сист. акс. Гильб. м. определить понятие вектора и ввести сложение векторов, умнож. вект. на число, скал. произведение и отклад. вект. от точки.
26. Сістэма аксіём Гільберта трохмернай эўклідавай прасторы. I яе параунанне з сiстэмай аксіём Вейля. Аксиоматика Гильберта в 1899г. основные объекты: «точка», «прямая», «плоскость». Основные отношения – «принадлежность» (или лежать на), «лежать между», «конгурентность». Объекты и основные отношения в аксиоматике Гильберта не описываются, а их взаимоотношения характеризуются определенной системой аксиом. Система аксиом Гильберта включает пять групп аксиом – аксиомы принадлежности, аксиомы порядка, аксиомы конгурентности, аксиомы непрерывности, аксиомы параллельности. I.Аксиомы принадлежности: 1)через любые две точки проходит прямая; 2)через любые две точки проходит не более одной прямой; 3)на каждой прямой лежит по крайней мере две точки. Существуют по крайней мере хотя бы три точки, не лежащие на одной прямой. 4)через любые три точки, не лежащие на одной прямой, проходит плоскость. На каждой плоскости лежит хотя бы одна точка. 5)через любые три точки, не лежащие на одной прямой, проходит не более одной плоскости. 6) если точки А и В прямой а лежат в плоскости а, то каждая точка прямой а лежит в плоскости а. в этом случае говорят, что прямая а лежит в плоскости а или плоскость а проходит через прямую а. 7)если две плоскости α и β имеют общую точку, то они имеют по крайней мере еще одну общую точку. 8)существуют 4 точки, которые не лежат в одной плоскости. На основании системы аксиом принадлежности можно доказать следующие теоремы: 1.Две прямые не могут иметь более одной общей точки. 2.две плоскости либо не имеют общих точек, либо имеют общую прямую. 3.через любую прямую и не лежащую на ней точку проходит единственная плоскость. Док-во. Пусть точка А не принадлежит прямой m. Докажем, что через А и m проходит единственная плоскость. 1)на прямой m сущ по крайней мере 2 точки (1.3)
2)точки А,В,С не лежат на одной прямой (если бы они лежали на одной прямой, получиили бы противоречие с условием) 3)через точки А,В,С проходит единственная плоскость (1.4,1.5) 4)В,С ϵ пл-ти а, значит, каждая точка m ϵ плоскости а (1.6) II.Аксиомы порядка: 0)точки на прямой находятся в отношении «лежать между». 1)если точка В лежит между точками А и С, тогда точки А,В,С различны и точка В лежит между С,А. 2)для любых двух точек А и В существует по меньшей мере одна точка С, такая что А-В-С. 3)среди любых трех точек прямой сущ не более одной точки, лежащей между двумя другими. Отрезком АВ наз пара точек А и В. Точки А и В наз концами отрезка. Точки, лежащие между А и В, назыв внутренними точками отрезка. Аксиома Паша.(аксиома 2.4) Пусть А,В,С – три точки, не принадлежащие одной прямой. Прямая l лежит в плоскости (АВС) и не проходит ни через одну из этих точек. Если прямая l проходит через внутреннюю точку отрезка АВ, то тогда она проходит либо через внутреннюю точку отр ВС, либо через внутр точку отр АС. Пользуясь группами аксиом I и II можно доказать следующие теоремы: из трех точек прямой только одна лежит между двумя другими. Межу любыми двумя точками прямой лежит счетное множество точек. III.Аксиомы конгурентности: 1)пусть дан отрезок АВ и луч с началом в точке A’, тогда существует точка B’ ϵ этому лучу, так что АВ=A’B’. 2)если A’B’ конгурентно (A’’B’’≡ A’B’), тогда A’B’≡АВ, A’’B’’≡АВ, значит, A’B’≡ A’’B’’. 3) Пусть А-В-С и A’-B’-C’. Если АВ≡ A’B’ и ВС≡B’C’, то АС≡A’C’. 4)пусть лан угол (h,k) и некоторая плоскость с границей l’, на которой дан луч k’ с началом в точке О’. тогда в данной полуплоскости существует луч h’, такой что угол (h,k)=(h’,k’). На основании аксиом I-III можно доказать теоремы о равенстве углов при основании у равнобедренного треугольника, теорему о внешнем угле треугольника. IV.Аксиомы непрерывности: 1)аксиома Архимеда: Пусть АВ и СD - произвольные отр., тогда на прямой АВ сущ. конечное число точек А1,А2..,Аn, таких что отрезки АА1,АА2,..,Аn-1An- кангр-ны отрезку CD и при этом т.В нах. между Аn-1 и Аn. 2)аксиома Кантора: пусть дана прямая и на ней бесконечная последовательность отрезков. Таких что каждый последующий лежит внутри предыдущего и для любого отр CD найдется такой номер n, что AnBn≤CD. Тогда найдется на прямой точка, которая принадлежит всем этим отрезкам.
На основании групп аксиом I-IV млжно доказать теорему о пересечении прямой и окружности, о пересечении двух окружностей. V.Аксиома параллельности: Пусть дана прямая а и точка не принадл. этой прямой. Тогда в пл-ти, определяемой этой прямой и точкой, через точку О можно провести не более одной прямой, не пересекающей прямую а. Используя аксиомы I-V можно обосновать теорию параллельности прямых, доказать теорему о сумме углов треугольника.
27. Сістэма натуральных лікаў. Система аксиом мн-ва нат-х чисел была предложена Джузэппе Пиано. Опр. Непустое мн-ва N наз. мн-вом натур-х чисел, когда на нем определено отношение между эл-тами этого мн-ва N “идет непосредственно за” (когда какой-то эл-т “идет непосредственно за” эл-том а, то его будем обозн. Опр .сложением 2-х нат. чисел наз. внутренняя бинарная операция + для которой выполняются 2 аксиомы: 1) Т. 1 Опр. Умножение 2-х нат. чисел наз. внутренняя бинарная операция Т. 1 Т. 3 Т.1 определим отношение Т. 2 Парядок на мн-ве нат. чисел явл. линейным, эт. зн., что Т. 3 З-ны монотонности: 1) Т. 4 З-ны сократимости: 1) Т. 5 Аксиома Архимеда: Т. 2 □ 28. Скалярны здабытак вектараў ў трохмернай эўклідавай прасторы.
|
||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.116.159 (0.011 с.) |
 При этом все акс. Вейля док-ся как теар. с точки зрения системы акс. Гильб. Это зн., что каждая теор., док-ная по Вейлю, м.б. док-на по Гильб-ту. Наоборот, с пом. сист. акс. Вейля м. ввести панятие прямой, пл-ти, определить понятия лежат между, кангр-ть. При этом кажн. акс. Гильберта явл. теор. По Вейлю, поэтому кажн. теор. по Гильб-ту явл. теор. по Вейлю. Можно сказать в этом смысле, что аксиоматика Гильб. и Вейля эквивал-ные.
При этом все акс. Вейля док-ся как теар. с точки зрения системы акс. Гильб. Это зн., что каждая теор., док-ная по Вейлю, м.б. док-на по Гильб-ту. Наоборот, с пом. сист. акс. Вейля м. ввести панятие прямой, пл-ти, определить понятия лежат между, кангр-ть. При этом кажн. акс. Гильберта явл. теор. По Вейлю, поэтому кажн. теор. по Гильб-ту явл. теор. по Вейлю. Можно сказать в этом смысле, что аксиоматика Гильб. и Вейля эквивал-ные.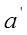 ) такой, что (аксиомы): 1)
) такой, что (аксиомы): 1) 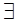 такой эл-т 1, который не “идет непосредственно за” ни за каким числом.
такой эл-т 1, который не “идет непосредственно за” ни за каким числом.  , 2) любое нат. число, кроме 1 “идет непосредственно за” только за одним нат. числом.
, 2) любое нат. число, кроме 1 “идет непосредственно за” только за одним нат. числом.  , 3) за каждым нат. числом “идет непосредственно за” только одно нат. число
, 3) за каждым нат. числом “идет непосредственно за” только одно нат. число  , 4) аксиома индукции: пусть
, 4) аксиома индукции: пусть  (подмн-во мн-ва) и а)
(подмн-во мн-ва) и а)  , б)
, б)  , тогда
, тогда  и
и  совпадают:
совпадают:  .
. , 2)
, 2)  .
. , Т. 2
, Т. 2  . Т. 3
. Т. 3  , Т. 4
, Т. 4 
 для которой выполняются 2 аксиомы: 1)
для которой выполняются 2 аксиомы: 1)  , 2)
, 2)  .
.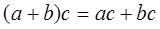 – дистриб-ць., Т. 2
– дистриб-ць., Т. 2 
 , Т. 4
, Т. 4 
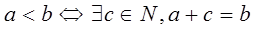 . Определенное отношение явл. отношением строгого порядка.
. Определенное отношение явл. отношением строгого порядка. выполняется только адно з 3-х условий: 1)
выполняется только адно з 3-х условий: 1)  , 2)
, 2)  3)
3)  .
. , 2)
, 2)  .
. , 2)
, 2)  .
. , что
, что 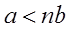 .
.

 ■
■


