
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 2. Решение различных видов дифференциальных уравнений первого порядкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§ 4. Уравнения первого порядка с разделяющимися переменными Определение Метод интегрирования Пример 1 Пример 2 § 5. Линейные дифференциальные уравнения первого порядка Определение линейного дифференциальное уравнение первого порядка Линейное однородное уравнение Решение Пример 3 § 6. Однородные дифференциальные уравнения первого порядка Определение однородного дифференциального уравнения первого порядка Метод решения Пример 4 § 4. Уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде
Правая часть этого уравнения представляет собой произведение двух множителей, каждый из которых является функцией только одного аргумента. Например, уравнение Точно так же, уравнение Напротив, уравнение Метод интегрирования уравнения с разделяющимися переменными заключается в следующем. 1. Приведем дифференциальное уравнение первого порядка к виду:
2. Умножим обе части уравнения на dx и поделим на
3. Интегрируя, получим:
Полученное выражение представляет собой общий интеграл уравнения с разделяющимися переменными. Пример 1. Решить уравнение Решение. Разрешая уравнение относительно производной, получим Умножим обе части уравнения на dx и поделим на у: Интегрируя, получим: Для упрощения полученного решения воспользуемся часто применяемым приемом: положим
Полагая
где С – произвольная постоянная. Пусть требуется теперь из найденного общего решения выделить частное решение, удовлетворяющее условию Таким образом, искомое частное решение имеет вид Пример 2. Приведем решение задачи об остывании тела (см. Задачу 1 из Лекции 1). Ранее, составляя математическую модель задачи, мы пришли к необходимости поиска частного решение дифференциального уравнения
Найдем общее решение уравнения. Умножим обе части уравнения на dt и поделим на (Т – 10):
Проинтегрируем полученное равенство:
Получили общее решение дифференциального уравнения. Для нахождения частного решения, воспользуемся начальным условием Т (0) = 100:
Подставив полученное значение
Полученное частное решение зависит от коэффициента пропорциональности k. В условии задачи он не определен, но его можно найти, если воспользоваться вторым начальным условием Т (10) = 60:
В результате, зависимость температуры от времени в заданных условиях имеет вид:
Теперь можно определить, через сколько минут температура тела станет равной 20 градусам, решив уравнение:
Таким образом, температура тела станет равной 20 градусам примерно через 37,4 минут.
§ 5. Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется линейным, если его можно представить в виде
где P (x) и Q (x) – заданные непрерывные функции от х (или постоянные). Название «линейное» не случайно, т.к. здесь и искомая функция, и ее производная находятся в первой степени (сравните с уравнением прямой линии: Например, уравнения Если Q (x) º 0, то линейное уравнение называется линейным однородным уравнением. Решение линейного дифференциального уравнение первого порядка ищут в виде произведения двух функций от х:
Полученные выражения подставим в уравнение
Перенесем первое слагаемое правой части в левую часть уравнения, сгруппируем слагаемые и вынесем за скобки общий множитель:
Далее возвращаемся к уравнению (*) и, решая его, как уравнение с разделяющимися переменными, находим функцию v:
Для решения уравнения достаточно найти какое-нибудь частное решение уравнение (**), поэтому выберем С 1 = 0, тогда
Подставим найденное значение функции v = v * в уравнение (2.2) и решим его:
Возвращаясь к формуле
Рассмотрим решение линейного дифференциального уравнение первого на примере. Пример. Решить уравнение Решение. Полагаем или
Группируем второе и третье слагаемые левой части уравнения и выносим за скобки общий множитель:
 . .
Пусть
Полагая С 1 = 0, получим: Учитывая, что
Окончательно имеем
§ 6. Однородные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде
Например, уравнения В однородном уравнении переменные вообще говоря не разделяются. Однако оно легко может быть преобразовано в уравнения с разделяющимися переменными. В этом заключается метод решения таких уравнений. Для разделения переменных введем новую функцию z, положив
В полученном уравнении переменные разделяются:
Найдя интеграл в левой части полученного уравнения и возвращаясь к первоначальной переменной у, получим общее решение однородного уравнения. Пример. Проинтегрировать уравнение Разрешим уравнение относительно производной:
Числитель и знаменатель правой части уравнения поделим на х 2, получим:
Делая подстановку
В полученном уравнении разделим переменные и найдем общее решение:
Положим
Получили общий интеграл уравнения.
Существует и другие методы решения различных уравнений первого порядка, но мы остановимся на рассмотренных выше. Использование этих методов для интегрирования уравнений будет отработано на практическом занятии. Дифференциальные уравнения
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.01 с.) |

 .
. есть уравнение с разделяющимися переменными, т.к. в нем можно принять
есть уравнение с разделяющимися переменными, т.к. в нем можно принять  и
и  .
. есть уравнение с разделяющимися переменными, т.к. его можно привести к виду
есть уравнение с разделяющимися переменными, т.к. его можно привести к виду  или
или  , где
, где  и
и  .
. нельзя представить в виде произведения двух множителей
нельзя представить в виде произведения двух множителей  , следовательно, оно не является уравнением с разделяющимися переменными.
, следовательно, оно не является уравнением с разделяющимися переменными. .
. , получим:
, получим: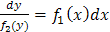 .
.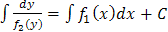 .
. .
. или
или  .
. .
. или
или  , где С 1 – произвольная постоянная.
, где С 1 – произвольная постоянная. (С 2 > 0). Тогда
(С 2 > 0). Тогда
 или
или 
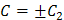 , окончательно получим
, окончательно получим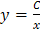 ,
, . Заменяя в общем интеграле
. Заменяя в общем интеграле 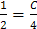 , откуда С = 2.
, откуда С = 2. .
. , при условиях Т (0) = 100, Т (10) = 60.
, при условиях Т (0) = 100, Т (10) = 60.

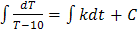





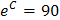 , откуда
, откуда  .
.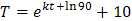




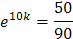
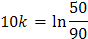

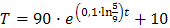 .
.


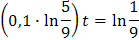

 ,
, ).
). и
и 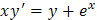 будут линейными, а уравнение
будут линейными, а уравнение  не является линейным.
не является линейным. или
или 
 .
. , получим:
, получим: .
.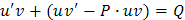
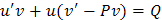
 .
. .
.







 .
. и
и  , получим ответ:
, получим ответ: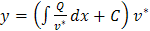 , где
, где  .
. , тогда
, тогда  .
.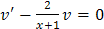 , тогда
, тогда

 .
. .
.


 .
.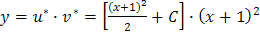 или
или
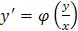 .
.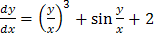 и
и  являются однородными. Уравнение
являются однородными. Уравнение  также однородное, т.к. деля числитель и знаменатель правой части на х 3, получим
также однородное, т.к. деля числитель и знаменатель правой части на х 3, получим  .
.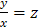 . Тогда y = x·z, следовательно,
. Тогда y = x·z, следовательно,  . В этом случае однородное уравнение примет вид:
. В этом случае однородное уравнение примет вид: .
. . Предполагая, что
. Предполагая, что  , получим:
, получим:
 .
. .
.

 и
и 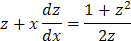




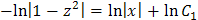


 , тогда
, тогда  . Возвращаясь к исходной переменной, произведем обратную замену
. Возвращаясь к исходной переменной, произведем обратную замену 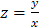 и получим:
и получим:





