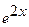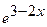Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение дифференциальных уравнений в ExcelСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теоретическая часть. Мощные вычислительные возможности электронной таблицы Microsoft Excel 7.0 для Windows 95 позволяют решать самые разнообразные задачи. В этой главе мы рассмотрим решение задачи Коши для обыкновенного дифференциального уравнения первого порядка. Помимо развитого аппарата формул и функций в состав Excel входит специальное средство для решения задач оптимизации — Пакета анализа. В этой главе мы покажем, как использовать этот инструмент Excel для решения линейных и нелинейных задач математического программирования.
Решение обыкновенного дифференциального уравнения первого порядка
В этом разделе мы решим задачу Коши для обыкновенного дифференциального уравнения первого порядка. В общем виде задача Коши формулируется следующим образом: найти решение y = y(x) дифференциального уравнения следующего вида: dy/dx = f(x,y) удовлетворяющее начальному условию y(0) = y0 Найдем решение дифференциального уравнения следующего вида: dy/dx = 2*y + exp(x) - x удовлетворяющее начальному условию: y(0) = 0,25 Решение нужно найти на отрезке [0,T], где параметр «T» может принимать любые значения. Точное решение этого уравнения имеет следующий вид: y(x) = exp(2*x) - exp(x) - x Нам нужно найти численное решение этого уравнения, то есть функцию заданную в табличном виде, принимающую решения на отрезке [0,T] с шагом h и сравнить его с точным решением в тех же точках. Определим шаг h по следующей формуле: h = T/N где N — числу точек на отрезке [0,T], в которых вычисляется значение искомой функции. Для решения поставленной задачи мы применим два метода: метод Эйлера и метод Рунге-Кутта 4-го порядка. Первый метод очень просто реализуется, а второй — гораздо точнее. Давайте коротко остановимся на каждом из этих методов. Метод Эйлера заключается в том, что решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка задается рекуррентной формулой следующего вида: yk+1 = yk + h*f(xk, yk) где xk = x0 + h*k, x0 = 0, k = 0, 1, 2,... N-1. Мы приводим метод Эйлера из-за простоты его реализации. Метод Рунге-Кутта 4-го порядка заключается в том, что решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка задается рекуррентной формулой следующего вида: yk+1 = yk + (m1 + 2*m2 + 2*m3 + m4)*h/6
где m1 = f(xk, yk) m2 = f(xk + h/2, yk + m1*h/2) m3 = f(xk + h/2, yk + m2*h/2) m4 = f(xk + h, yk + m3*h), k = 0, 1, 2,... N-1.
Метод Рунге-Кутта значительно точнее метода Эйлера, но и программировать его сложнее, однако мощный аппарат формул электронной таблицы Microsoft Excel позволяет сравнительно просто организовать процесс вычисления. Графические возможности Excel позволяют сравнить приближенное и точное решение, что также будет отражено в следующих разделах.
Алгоритм численного решения В колонке I у нас будут находится границы отрезке [0,T]. В начале расчетов положим I1 = 0 (это величина левой границы отрезка [0,T]), I2= 1 (это величина T правой границы отрезка [0,T]), в ячейке I3 вычисляется величина шага h по формуле следующего вида: = (I2 - I1)/N В ячейке I4 находится число точек N = 100.
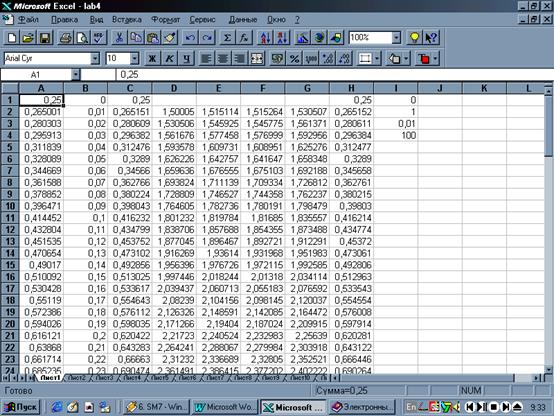
Рисунок 1 - Решение дифференциального уравнения методом Эйлера и методом Рунге-Кутта 4-го порядка
В колонке A вычисляется решение нашей задачи по формуле Эйлера. В ячейке A1 находится начальное значение y0 = 0,25. В ячейку A2 введем формулу следующего вида: =A1+$I$3*(2*A1+EXP(B1)-B1) В колонке B будет находиться текущее значение переменной x. В ячейках B1 и B2, соответственно, находятся формулы следующего вида: =I1 =B1+$I$3 В ячейку B1 пересылается левая граница отрезка [0,T], а в ячейке B2 прибавляется величина шага h из ячейки I3 к значению в предыдущей ячейке B1. В колонке C вычислим точное решение. В ячейке C1 находится значение решения в точке x = 0, а в ячейке C2 формула следующего вида: =EXP(2*B2)-EXP(B2)+B2. Эта формула вычисляет значение точного решения уравнения при значении аргумента x из ячейки B2. В колонке H вычисляется значение численного решения задачи Коши методом Рунге-Кутта 4-го порядка. Значение xk берется их ячейки B2, а значение yk берется из ячейки H1. В ячейке H2 записана формула следующего вида: =H1+(D2+2*E2+2*F2+G2)*$I$3/6 В ячейках D2, E2, F2 и G2 записаны формулы для коэффициентов m1, m2, m3 и m4, соответственно. Эти формулы имеют следующий вид: =2*H1+EXP(B1)-B1 =2*(H1+D2*$I$3/2)+EXP(B1+$I$3/2)-B1-$I$3/2 =2*(A1+E2*$I$3/2)+EXP(B1+$I$3/2)-B1-$I$3/2 =2*(A1+F2*$I$3)+EXP(B1+$I$3)-B1-$I$3
Распространим формулы из 2 строки до значения x = 1. В соответствующей ячейке столбца B должно находится число 1. Последняя строка имеет номер 101. Результат распространения представлен на рисунок 1. Алгоритм вычисления значений решения задачи Коши реализован. Проведем расчеты и построим графики.
Мы будем изменять значение правой границы отрезка [0,T], а число точек, в которых вычисляются значения решения, оставим без изменения. Это даст нам возможность показать влияние величины шага на точность полученного решения. Построим графики точного и приближенного решения задачи Коши. Напомним, что в колонке A получено решение методом Эйлера, колонке H — методом Рунге-Кутта 4-го порядка, в колонке C — точное решение, а в колонке B находятся значения переменной x. Колонка B будет играть роль меток. При построении графиков она должна быть самой левой в блоке данных. Чтобы добиться такого положения, при построении графика выделим блок B2:E4, содержащий 4 колонки. При этом самая левая колонка — столбец B. В столбце C находится точное решение задачи, столбцы C и D мы включили только для того, чтобы заменить их в блоке на колонки A и H. Ниже приведена последовательность действий при построении графика: Нажмите кнопку Мастер диаграмм и выделите место для построения графика.
Рисунок 2 -Установка диапазона данных
В окне диалога «Мастер диаграмм шаг 1 из 5» установите диапазон данных, по которым будет строится диаграмма. Для этого выделите мышью ячейки B2:E2. В поле ввода Диапазон появится ссылка $B$2:$E2. Наш блок ячеек простирается до 101 строки. Поскольку перемещать указатель мыши так далеко вниз неудобно, нажмите мышью в поле ввода Диапазон и исправьте последнюю цифру 2 на число 101 (рисунок 2). После этого нажмите кнопку Далее>. В окне диалога «Мастер диаграмм шаг 2 из 5» выберите тип диаграммы График и нажмите кнопку Далее>. В окне диалога «Мастер диаграмм шаг 3 из 5» выберите формат графика «2» и нажмите кнопку Далее>. В окне диалога «Мастер диаграмм шаг 4 из 5» установите один столбец под метки оси X и нажмите кнопку Далее>. В окне диалога «Мастер диаграмм шаг 5 из 5» установите переключатель Добавить легенду и нажмите кнопку Готово. На экране появится диаграмма. Сразу же приступаем к замене 2 и 3 рядов данных столбцами H и A, соответственно. Дважды нажмите на диаграмме, чтобы войти в режим ее редактирования. Значения в рядах 2 и 3 настолько близки, что визуально неотличимы на графике, поэтому заменим выделенный ряд, не заботясь о его содержимом. Установите указатель мыши на линии рядов 2 и 3 и нажмите мышью. На ряде данных 3 появились черные квадратики (рисунок 3). В строке ввода появилась ссылка на ряд, по которой мы определили его номер.
Рисунок 3 - Подготовка к замене ряда 3
Установите указатель мыши около одного из квадратиков и нажмите правую кнопку мыши. Появится меню, из которого выберите команду Формат ряда. Появится окно диалога «Форматирование ряда», в котором выберите вкладку «Значения Y».
Рисунок 4 - Изменение ряда данных 3 во вкладке «Значения Y»
В поле ввода Значения Y введите ссылку на ячейки H2:H101 с численным решением задачи Коши, полученным по методу Рунге_Кутта 4-го порядка. Для этого достаточно просто исправить буквы E на H в поле ввода (рисунок 4). Если нажать кнопку OK, то форматирование ряда закончится. Поскольку цветные линии плохо различимы при печати, изменим тип и цвет линии ряда 3. Для этого выберите вкладку «Вид». В области «Линии» установите цвет линии — черный, тип — пунктир (рисунок5). Нажмите кнопку OK. На рисунке 5 показан результат замены ряда данных 3. Тот факт, что ряды 1 и 3 почти совпадают означает, что точное решение задачи Коши (ряд 1) и численное решение полученное по методу Рунге-Кутта 4-го порядка (ряд 3) практически совпадают.
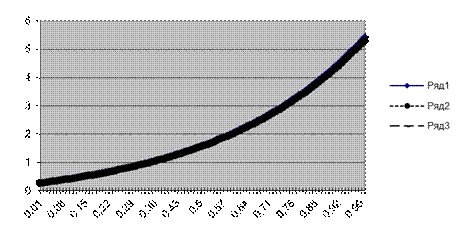
Сделаем замену значений для ряда 2. Подставим вместо столбца D столбец A. Изменим цвет линии на черный, а тип линии — на штрих-пунктирный. Результат показан на рисунке 5. Вывод здесь однозначен: на отрезке [0,1] графики точного решения и решений полученных численными методами при шаге 0,01 отличаются незначительно.
Рисунок 5 - Графики точного и приближенных решений задачи Коши на отрезке [0,1]
Процесс построения графиков закончен. Теперь изменим отрезок интегрирования задачи Коши. Найдем решение на отрезке [0,10]. Для этого введем в ячейку I2 число 10. Расчет формул и построение нового графика произойдет автоматически (рисунок 6).
Рисунок 6 - Решение задачи Коши на отрезке [0,10]
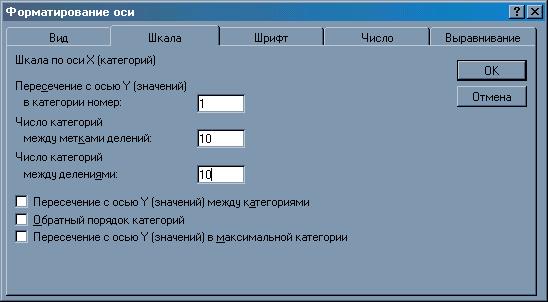
Отформатируем оси графика. Для этого выполните следующие действия: - Войдите в режим редактирования графика. - Нажмите мышью на оси X. На концах оси появятся квадратики. - Нажмите правую кнопку мыши и в появившемся меню выберите команду Формат оси - Появится окно диалога «Форматирование оси». - Выберите вкладку «Шкала» и установите число категорий между метками делений и между делениями по 10 (рисунок 7).
Рисунок 7 - Форматирование оси X
Нажмите кнопку OK. Ось X отформатирована. Приступаем к форматированию оси Y. Целью форматирования является получение удобного для чтения формат чисел на оси Y. Поскольку по оси Y отображаются большие значения, введем логарифмическую шкалу для этой оси. Для этого в окне диалога «Форматирование оси» выберите вкладку «Шкала» и установите флажок Логарифмическая шкала (рисунок 8). После нажатия кнопки OK график изменится. Новый график представлен на рисунок 9. На нем изменены размеры и формат основания.
Рисунок 8 - Форматирование оси Y
Рисунок 9 - График с логарифмической шкалой
Проверка на точность
При вычислении с шагом 0,01 на отрезке [0,1] точное решение задачи Коши очень близко к численному решению. Однако отличие все -таки есть. Рассмотрим влияние шага h на точность вычислений. Для этого получим решение задачи Коши на отрезке [0,10] с шагом 0,5 и сравним полученные решения между собой и результатами, приведенными на рисунке 10. Графики точного и численных решений с шагом h=0,5 представлены на рисунке 10. На этом рисунке уже отчетливо видно, что метод Рунге-Кутта 4-го порядка (ряд 3) имеет более высокую точность по сравнению с методом Эйлера (ряд 2).
Рисунок 10 - Решение задачи Коши на отрезке [0,10] с шагом 0.5.
Задания к лабораторной работе. 1. Решите, используя методы Эйлера и Рунге-Кутта дифференциальные уравнения согласно варианту задания, представленному в таблице 1. 2. Постройте график, отображающий точное решение, решение методом Эйлера и методом Рунге-Кутта.
Содержание отчета Постановка задачи, методика решения дифференциальных уравнений средствами Excel, результаты выполнения, выводы.
Контрольные вопросы. 1. Какие данные необходимо ввести в таблицу для решения задачи Коши? 2. Какие данные необходимо исправить в формулах при их распространении в таблице? 3. Как отобразить решение диф. уравнений на диаграмме? Какие изменеиня следует внести в формат диаграммы?
Таблица 1 - Варианты заданий на лабораторную работу
Лабораторная работа №5.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 8159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.35.247 (0.01 с.) |


















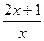



 = 0
= 0





 = 0
= 0