Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач математического программирования в ExcelСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теоретическая часть Примеры задач математического программирования
Задача об использовании сырья.
Предположим, что для изготовления продукции четырех типов Прод1, Прод2, Прод3, Прод4 требуются ресурсы трех видов: трудовые, сырье и финансы. Запасы ресурса каждого вида ограничены. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, запасы ресурсов, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 1.
Таблица 1 - Исходные данные задачи об использовании сырья
Требуется составить такой план выпуска продукции всех типов, при котором доход предприятия от реализации всей продукции оказался бы максимальным.
Математическая модель задачи имеет вид:
где xj – количество выпускаемой продукции j -го типа; F – линейная функция цели, представляющая собой доход, получаемый предприятием; три линейных неравенства составляют систему ограничений задачи. В левых частях неравенств указаны величины расхода ресурса при выпуске продукции, а правые части показывают количество имеющегося ресурса, т.е. его ограниченные запасы. Расходы ресурсов при выпуске продукции не должны превысить имеющиеся запасы, поэтому неравенства имеют знак ≤. Таким образом, смысл задачи о распределении ресурсов таков: среди неотрицательных решений xj системы (1) выбрать такое, при котором функция цели F принимает наибольшее значение (максимизируется).
Задача о составлении смеси. Для сохранения здоровья и работоспособности человек должен потреблять в сутки некоторое количество питательных веществ, например, белков, жиров, углеводов, воды и витаминов. Пусть эти вещества поставляются в двух видах пищи П1 и П2. Содержание полезных веществ в единице веса каждого вида пищи показано в таблице 2. Там же указаны минимальные суточные нормы питательных веществ, а также стоимости единицы веса пищи П1 и П2.
Таблица 2 - Исходные данные задачи о смеси
Требуется так организовать питание, чтобы стоимость его (смеси или сочетания продуктов) была наименьшей, но человек получил бы не менее минимальной суточной нормы полезных веществ всех видов. Пусть xj , ( Тогда общая стоимость питания F равна
Содержание жиров в смеси двух продуктов составляет
и не должно быть меньше минимальной суточной нормы, равной 10. Это требование приводит к неравенству
Аналогично составляются неравенства для остальных питательных веществ. Итак, математическая формулировка задачи о смеси имеет вид:
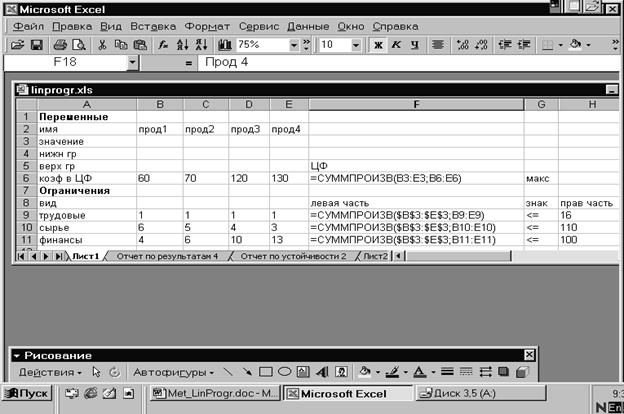
Решение задач математического программирования Ввод условий задачи. Решение задачи математического программирования в Excel рассмотрим на примере задачи об использовании сырья. Для решения задачи с помощью Excel следует создать форму для ввода исходных данных и ввести их. Форма ввода показана на рисунке 1а. В ячейку F6 введено выражение целевой функции как суммы произведений значений прибыли от выпуска единицы продукции каждого типа на количество выпускаемой продукции соответствующего типа. Для наглядности на рисунок 1б представлена форма ввода исходных данных в режиме вывода формул. В ячейки F8:F10 введены левые части неравенств-ограничений для ресурсов каждого вида. Строка с заголовком «нижн гр» содержит нулевые значения, т.к. переменные
а)
б) Рисунок 1 - Ввод исходных данных задачи об использовании сырья
Поиск решения Для решения задач линейного программирования в Excel используется мощный инструмент, называемый Поиск решения. Обращение к Поиску решения осуществляется из меню Сервис, на экран выводится диалоговое окно Поиска решения (рисунок 2).
Рисунок 2 - Окно Поиска решения
Ввод условий задачи для поиска ее решения состоит из следующих шагов: 1. Назначить целевую функцию, для чего установить курсор в поле Установить целевую ячейку окна Поиск решения и щелкнуть в ячейке F6 в форме ввода; 2. Включить переключатель значения целевой функции, т.е. указать ее Равной Максимальному значению; 3. Ввести адреса изменяемых переменных (xj): для этого установить курсор в поле Изменяя ячейки окна Поиск решения, а затем выделить диапазон ячеек B3:E3 в форме ввода; 4. Нажать кнопку Добавить окна Поиск решения для ввода ограничений задачи линейного программирования; на экран выводится окно Добавление ограничения (рисунок 3): - ввести граничные условия для переменных xj (xj³0), для этого в поле Ссылка на ячейку указать ячейку В3, соответствующую х1, выбрать из списка нужный знак (³), в поле Ограничение указать ячейку формы ввода, в которой хранится соответствующее значение граничного условия, (ячейка В4), нажать кнопку Добавить; повторить описанные действия для переменных х2, х3 и х4; - ввести ограничения для каждого вида ресурса, для этого в поле Ссылка на ячейку окна Добавление ограничения указать ячейку F9 формы ввода, в которой содержится выражение левой части ограничения, наложенного на трудовые ресурсы, в полях Ограничение указать знак £ и адрес Н9 правой части ограничения, нажать кнопку Добавить; аналогично ввести ограничения на остальные виды ресурсов; - после ввода последнего ограничения вместо Добавить нажать ОК и возвратиться в окно Поиск решения.
Рисунок 3 - Окно ввода ограничений
Для решения задачи нажать кнопку Выполнить в окне Поиск решения, на экране – окно Результаты поиска решения (рисунок 4), в котором содержится сообщение Решение найдено. Все ограничения и условия оптимальности выполнены. Если условия задачи несовместны, то выводится сообщение Поиск не может найти подходящего решения. Если целевая функция не ограничена, то появляется сообщение Значения целевой ячейки не сходятся.
Рисунок 4 - Окно результатов поиска решения задачи математического программирования
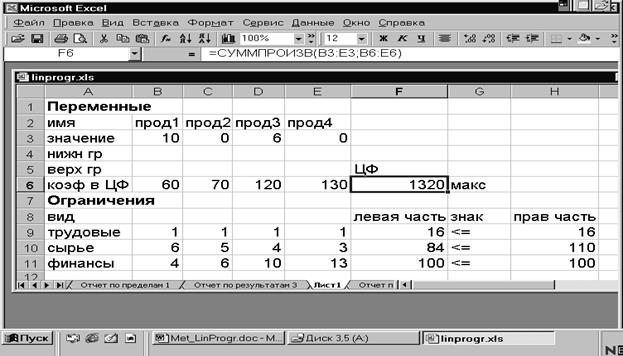
Для рассматриваемого примера решение найдено и результат оптимального решения задачи выводится в форме ввода: значение целевой функции, соответствующее максимальной прибыли и равное 1320, указывается в ячейке F6 формы ввода, оптимальный план выпуска продукции х1=10, х2=0, х3=6, х4=0 указывается в ячейках В3:С3 формы ввода (рисунок 5). Количество использованных для выпуска продукции ресурсов выводится в ячейки F9:F11: трудовых – 16, сырья – 84, финансов – 100. С помощью окна Результаты поиска решения можно получить отчет по результам решения: Для вызова отчета в поле Тип отчета выделить пункт Результаты и нажать ОК. Отчет по результатам (рисунок 6) состоит из трех таблиц: - таблица 1 содержит сведения о целевой функции; в столбце Исходно указывается значение целевой функции до начала вычислений; - таблица 2 содержит значения искомых переменных xj, полученных в результате решения задачи (оптимальный план выпуска продукции); - таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий. Для Ограничений в графе Формула приведены зависимости, которые были введены при задании ограничений в окне Поиск решения; в графе Значение указаны величины использованного ресурса; в графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние выводится сообщение связанное; при неполном использовании ресурса в этой графе указывается не связан.
Рисунок 5 - Результаты решения задачи об использовании сырья
Рисунок 6 - Отчет по результатам решения задачи об использовании ресурсов
Для значений переменных xj приводятся аналогичные величины с той лишь разницей, что вместо неиспользованного ресурса показана разность между значением переменной xj в найденном оптимальном решении и заданным для нее граничным условием (xj³0).
Задание на лабораторную работу. Решить задачу математического программирования согласно варианту. Варианты задач представлены в таблице 3. Исследовать, как меняется оптимальное решение в зависимости от коэффициентов целевой функции; от свободных членов неравенств-ограничений.
Содержание отчета Постановка задачи, методика нахождения оптимального решения средствами Excel, результаты выполнения, выводы.
5. Контрольные вопросы -Какие средства имеются в среде Excel для поиска оптимальных решений? -Какие параметры следует определить в окне «Поиск решения»? -Что является признаком того, что решение задачи не существует?
Таблица 3 - Варианты задач математического программирования.
Продолжение таблицы 3
Продолжение таблицы 3
Библиографический список 1. Новиков Ф., Яценко А. Microsoft office в целом. – Санкт-Питербург.: BHV, 1996.-426 c.
2. Додж М. и др. Эффективная работа с Excel 7.0 – Санкт-Питербург.:Питер, 1997.- 313 с. 3. Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0.- – Санкт-Питербург.: BHV, 1997.-384 c. 4. Пейдж Дж. MathCad 6.0 в примерах и задачах. – Киев.: Бином, 1997.- 214 с.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.200.56 (0.011 с.) |

 , (1)
, (1) ) – потребляемое количество пищи видов П1 и П2.
) – потребляемое количество пищи видов П1 и П2. .
.
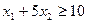 .
. (2)
(2)
 .
. должны быть неотрицательными по условию задачи, следовательно, наименьшее значение, которое они могут принять, равно 0. Верхних граничных значений переменные
должны быть неотрицательными по условию задачи, следовательно, наименьшее значение, которое они могут принять, равно 0. Верхних граничных значений переменные