
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложности решения дискретных задачСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте МЕТОДИЧЕСКОЕ ПОСОБИЕ по дисциплине Теория сложности вычислений для студентов 2 курса дневной (заочной) и экстернатной формы обучения направления 0802 Прикладная математика специальностей 6.080200 Информатика, 6.080200 Прикладная математика Симферополь, 2004 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ АЛГОРИТМИЧЕСКОЙ СЛОЖНОСТИ РЕШЕНИЯ ДИСКРЕТНЫХ ЗАДАЧ Учебно-методическое пособие для студентов факультета математики и информатики
Введение
С появлением компьютеров алгоритмические методы решения задач стали развиваться столь стремительно, что вызвали появление ряда новых, ярких теоретических направлений в математике. К таким направлениям следует отнести теорию сложности решения дискретных задач, основания которой были заложены в работах С. Кука (1971), Р. Карпа (1972) и А.А. Левина (1973) [7-9]. Только после возникновения этой теории (основанной на понятиях NР- полных и NР- трудных задач) многие математики-исследователи осознали бесперспективность поиска эффективных (существенно отличных от переборных) алгоритмов решения многих, важных задач: минимизации дизъюнктивных нормальных форм, задачи целочисленного линейного программирования общего вида, задачи коммивояжера, раскраски графа, нахождения корней полиномов над полем GР(2) и многих других. Оказалось, что указанные задачи являются универсальными переборными задачами в том смысле, что эффективное решение хотя бы одной из них повлечет открытие эффективных алгоритмов решения для всех остальных. В монографии К. Гари и Д. Джонсона [1] приведен список более 300 таких универсальных переборных (NР-полных задач), связанных с теорией графов, математической логикой, алгеброй, дискретной оптимизацией и другими.разделами математики. Изучив теорию NР-полных задач, математик получает на вооружение замечательный аппарат, с помощью которого, приступая и решению новой задачи, во многих случаях можно заранее оценить ее сложность и целесообразность поиска точного алгоритма ее решения за приемлемое число шагов. Теория NР-полных задач достаточно сложна для понимания, и ее изучения основ теории сложности, но для освоения материала понадобится знакомство с теорией функций алгебры логики, теорией алгоритмов, элементами теории графов и исследования операций. Поэтому пособие предназначается, прежде всего, для студентов старших курсов и аспирантов математического факультета. Учитывая важность простых приближенных алгоритмов решения дискретных экстремальных задач и различных эвристических методов, при изучении теории сложности полезно ознакомиться с возможностями алгоритмов «пожирающего» типа (GREEDY). Поэтому в пособии изложены основы теории матроидов и теорема Радо-Эдмондса.
Алгоритм Понятие алгоритма - одно из центральных в математике и, по крайней мере, не менее важное, чем понятие функции. Функция – это соответствие между двумя множествами X и У, согласно которому для каждого элемента Например, функция Лапласа:
полностью определена выражением (1.1) для любого Алгоритм принципиально отличается от функции тем, что устанавливая соответствие Главный элемент, необходимый для строгого определения алгоритма - это набор (множество) элементарных действий, из которых строятся конечные последовательности шагов. Математики, занимавшиеся формализацией понятия алгоритма, предложили pяд способов выбора множества элементарных действий и, соответственно, формальных моделей, уточняющих интуитивное понятие алгоритма. Наиболее удачные формализации понятия алгоритма были разработаны А.А. Марковым (элементарные действия - подстановки), А. Тьюрингом (элементарные действия - команды абстрактной математической машины), Э.Постом, М.Минским. Впоследствии оказалось, что разработанные этими математиками модели алгоритмов эквивалентны в том смысле, что классы решаемых с их помощью задач совпадают. В связи с этим А. Черч сформулировал гипотезу, известную как Тезис Черча, смысл которой состоит в том, что класс задач, решаемых в любой из построенных математиками формальных моделей алгоритмов, и есть класс всех задач, которые могут быть решены “интуитивно алгоритмическими” методами. Для математиков-программистов несложно переписать алгоритм решения задачи, подготовленный на одном языке программирования, на другой язык. Если такая трансляция, скажем, с языка PASCAL на С++ является делом достаточно простым, то трансляция тьюринговского алгоритма в марковский может оказаться значительно сложнее. Но есть одно обстоятельство, которое существенно снижает значение того, в какой формальной или прикладной системе (ЭВМ, язык) записан алгоритм. Пусть в системе Множества X и У такие, что Поскольку коэффициент Математики, занимающиеся исследованиями в области теории алгоритмов, чаще всего используют частично-рекурсивные функции и машину Тьюринга, хотя не исключаются и другие алгоритмические модели и языки, вплоть до некоторым образом «расширенных» языков программирования высокого уровня. Используя машину Тьюринга, математик может легко оценивать не только число шагов выполнения алгоритма как показатель «временной» сложности, но и число использованных ячеек тьюринговской ленты как показатель «обьемной» сложности или требуемого объема памяти. В терминах машины Тьюринга (МТ) как алгоритмической системы можно сформулировать следующие важные определения. Пусть
Класс NР - полных задач Ниже излагаются основы теории сложности, заложенной в основополагающих работах С. Кука [7], Р. Карпа [8], А.А. Левина [9]. Важно обратить внимание на полиномиальное преобразование задач как главный элемент этой теории. Известно, например, что задача о максимальном потоке в сети может быть преобразована в задачу линейного программирования. Подобные преобразования задач иногда оказываются полезными для нахождения решений, и для их осуществления приходится производить некоторые вычисления, связанные с перекодированием начальной информации и ответа - решения задачи (рис. 4.1). Определение 4.1. Задачи множества Z полиномиально сводимы к задачам множества S (обозначение - Zµ S), если существует функция j. вычисляемая за полиномиальное время и преобразующая любую задачу zÎ Z в задачу j(z) = s, sÎ S, причем zÎ Z • j(z)Î S
Вход Вход Выход Выход задачи задачи задачи задачи
Z j(z) j(z) Z
Рис. 4.3. Схема полиномиальной сводимости задачи Z к задаче j(z).
Множество всех NР- полных задач часто обозначают NPС (Nondeterministic Polinoyal Compete). Из определения 4.2. следует, что NPСÌ NP и NP-полные задачи являются наиболее сложными в классе NP: если хотя бы одну NP-полную задачу удалось решить за полино-миальное время, то и все задачи из NP (в силу полиномиальной своди-мости Z µ Z*) также удалось бы решить за полиномиальное время. Теорема 4.1 [1]. 1)Если 2) Если 3) Если Теорема 4.1 указывает способ доказательства. NР-полноты некоторой задачи Z, если известна хотя он одна NР -полная задача Z*: достаточно доказать, что Изучение сложности дискретных задач началось с исследования задач вычисления (или распознавания) свойств. Эти задачи для допустимой начальной информации могут иметь решение, представ-ляющее собой ответ «да» или «нет» (1 или 0). Например, имеет ли данный конечный граф хотя бы один гамильтонов контур, является ли совместной система линейных неравенств с целочисленными переменными и тому подобные задачи. В последствии результаты исследования сложности задач вычисления свойств были распространены и на другие, в частности оптимизационные задачи. Рис.4.2 Теоретико - множественная диаграмма класса NP в предположении что P¹ NP. Рис. 5.1 Вычисления при любом допустимом значении объекта у происходят в зоне ленты [-Т, Т] и завершаются не более чем за Т шагов (тактов работы НДМТ). Машина начав работу в конфигурации Построим КНФ Ф, такую, что любая задача проверки (распознания) свойства - в общем виде: - полиномиально сводится к проверке выполнимости КНФ Ф = В & C & D & Е & F & G, где В, С, D, E, f, g - дизъюнкты, имеющие следующий смысл: В = 1 • на каждом шаге головка машины обозревает ровно одну ячейку ленты:
С = 1 • в каждой ячейке на каждом шаге записан в точности один символ; D = 1 • на каждом шаге работы машина находится ровно в одном состоянии; Е = 1 • начальная конфигурация машины имеет вид F = 1 • машина работает по тьюринговской программе; G = 1 • заключительная конфигурация машины имеет вид если Р(х,у) = 1. Обозначим и внутренний алфавиты НМДТ; t - шаги выполнения алгоритма,
Введем следующие логические переменные:
иначе эта переменная равна нулю.
номером s, иначе эта переменная равна нулю. Используя введенные логические переменные, можно записать в виде формул следующие логические условия;
никакие две одновременно, т. к. Тогда
В начальном положении (t=0) головка машины обозревает ячейку с номером 1 в состоянии q1, а в первых n - ячейках записаны символы слова Х = х(1)...х(n), за ним - разделительный знак «*», после чего - слово Y и далее - пустые ячейки. Выполнение такой начальной конфигурации равносильно Е = 1, где
где l - пустой символ. Полиномиальная программа проверки свойства состоит из тьюринговских команд:
Другие NР- полные задачи.
После открытия С. Куком «первой» NР- полной задачи стало воз-можным доказывать NР- полноту других задач, NР- полными оказа- лись: задача выполнимости 3-КНФ, когда в выражении каждая дизъюнкция
задача о вершинном покрытии графа, о существовании гамильтонова цикла в графе, задача коммивояжера в экстремальной постановке, задача целочисленного линейного программирования, задача минимизации дизъюнктивной нормальной формы произвольной булевой функции, задача синтеза бинарного решающего дерева с минимальным числом листьев и многие другие [1]. Важно учитывать, что доказательство NР- полноты всегда произ-водится для любой исходной информации, допустимой для рассматри- ваемой задачи. При этом вполне возможно, что для некоторых исходных данных задача окажется полиномиально разрешимой: известны разрешимые с полиномиальной сложностью частные случаи для задачи минимизации ДНФ монотонной булевой функции, задачи целочис-ленного линейного программирования и многие другие. Задача называется NР- трудной, если к ней полиномиально сводится какая-нибудь NР- полная задача. Класс всех NР- трудных задач обозначают NРН. Задача z Î NРH по крайней мере так же трудна, как и любая задача из NР, но классу NР может не принадлежать. Практическое применение теории NР- полных задач позволяет при изучении каждой новой трудно решаемой задачи определить, целесообразно ли продолжать отыскивать точный эффективный алго-
ритм ее решения. Для этого необходимо установить, принадлежит ли задача классу NРС или NPH. Если такая принадлежность имеет место, то, возможно, имеет смысл искать её приближенное решение, опреде-ляемое следующим образом. Пусть требуется найти экстремум функции f(x) при условии х Î W, Если ε - приближенным называют любое решение х, удовлетворяющее неравенству
Практически важным является выделение подклассов задач из NРС. для которых нахождение ε - приближенных решений позволяет понизить сложность настолько, чтобы перевести решаемую задачу в класс Р. Существенной является и возможность работы с какой - либо одной задачей из NРС для изучения общих подходов к решению; часто в качестве таковой выбирают задачу коммивояжера, задачу минимизации ДНФ. Теория NР - полных задач, как видно из изложенного выше, опе-рирует с задачами вычисления свойств. Поэтому нужно отметить при-менимость теории к дискретным оптимизационным задачам. Если в оптимизационной задаче среди всех структур данного типа ищется структура, имеющая минимальную «стоимость» (например, среди всех маршрутов отыскивается маршрут минимальной длины, как в задаче коммивояжера), то этой задаче можно сопоставить задачу распоз-навания (вычисления) свойства, в котором в качестве дополнительного параметра фигурирует числовая граница В, а вопрос ставится о сущест-вовании структур данного типа, стоимость которых не превосходит В (например, маршрут длины не более В). Задача распознавания не может быть сложнее соответствующей задачи оптимизации. Действительно, имея маршрут минимальной дли-ны и длину этого маршрута, для решения задачи распознавания свой-ства нужно только сравнить ее с заданной границей В. Поэтому если задача вычисления свойства полной, то и задача, Если значения функции f(x) целочисленные и
Пример доказательства NP- полноты задачи методом сведения.
Пусть Г =(Х,U) - конечный граф, Х - множество вершин графа, U - множество дуг. Не теряя общности, можно обозначить вершины натуральными числами: Х = {1,2,..., n}, а дуги задать булевой матрицей Граф называют полным, если любые его две вершины соединены дугой. Граф Задача о полном подграфе состоит в том, чтобы по заданному графу Г выяснить, существует ли в Г полный подграф с Теорема 7.1. Задача о полном подграфе является NP- полной, Доказательство. Для удобства обозначим задачу о полном подграфе информацией о задаче /* Предположим, k-полный подграф существует */ УСПЕХ:= TRUE; /* Недетерминированный выбор k вершин */ Set:= [1..n]; for i:= 1 to k dо begin node:= сhoose(Sеt); v[i]:= node; Set:=Set\(nodе); еnd; /* Полиномиальная проверка */ for i:= 1 tо k-1 do for j:= i+1 tо k dо if u(v[i],v[j])=0 then УСПЕХ:=FALSE; write(УСПЕХ); Очевидно, что сложность приведенной N-программы может быть оценена как О(n(n-1)/2), т.е. полиномиально, откуда следует, что
б) Докажем, что
Пусть
есть произвольная k скобочная КНФ. Поставим во взаимно-однозначное соответствие каждому литералу из Ф вершину некоторого графа Г. Этот граф будет содержать номером скобки, в которую этот литерал входит, т.е. парой
Соединим дугой те, те и только те пары полученных вершин
для которых одновременно выполняются два условия: а) б) Таким образом, построен граф Г =(X,U) с указанными вершинами и дугами. Предположим, - что Ф - выполнима и Обратно, пусть граф Г полный подграф с k вершинами
зададим переменным с номерами
если k < n, зададим произвольно, получая набор
Поскольку эти литералы соответствуют вершинам полного подграфа, то они относятся к разным скобкам КНФ Ф, откуда следует, что Теорема доказана.
Список NР- полных задач.
Ниже приведена лишь небольшая часть задач. NР- полнота кото-рых установлена [1]. Эти задачи могут использоваться для доказа-тельства NР- полноты других задач и представляют известный прак-тический интерес. 8.1. Задача выполнимости КНФ. 8.2. Задача выполнимости 3-КНФ, когда дизъюнкция КНФ содержит не более 3 литералов. 8.3. Задача построения минимальной дизъюнктивной нормальной формы. 8.4. Истинность булевой формулы с кванторами вида
где
один из кванторов " или $. F 8.5. Задача о существовании конечного автомата не более чем с k внутренними состояниями, распознающего заданное подмножество последовательностей. 8.6. Существование бинарного дерева (БРД) решений не более чем с m листьями и задача синтеза БРД с минимальным числом листьев. 8.7. Задача о существовании вершинного покрытия графа мощности k. 8.8. Задача о раскраске графа в k цветов (каждая пара вершин, соеди-ненных дугой, - в разные цвета). 8.9. Задача о существовании гамильтонова цикла в графе и задача коммивояжера. 8.10. Задача распознавания в заданном графе Г1 подграфа, изо-морфного заданному графу Г2. 8.11. Задача о существовании в графе с размеченными дугами разреза с суммой весов дуг не меньшей k. 8.12. Задача о многопроцессорном расписании с заданным дирек-тивный сроком. 8.13. Задача составления учебного расписания. [1, стр. 311]. 8.14. Задача целочисленного линейного программирования, 8.15. Задача о ранце (иногда называется также задачей о рюкзаке). 8.16. Разрешимость квадратных диофантовых уравнений. 8.17. Разрешимость алгебраического уравнения и поле GF(2). 8.18. Задача о покрытии множества не более чем k его подмно- жествами.
Содержание Введение. 3 1. Алгоритмы. 4 2. Класс Р и эффективные вычисления 7 3. Недетерминированные алгоритмы и класс NP 9 4. Класс NР- полных задач 12 5. Теорема Кука: первая NР- полная задача 14 6. Другие NР- полные задачи 21 7. Пример доказательства NР- полноты задачи, методом сведения 24 8. Список NР- полных задач. 27 9. Матроиды и жадные алгоритмы. 28
Список рекомендованной литературы. 1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. -М.: Мир,1982,416 с. 2. Компьютер и задачи выбора. / под ред. академика Ю.И. Журавлева. - М.: Наука, 1989, 207 с. 3. Лекции по теории графов / Емеличев В.А., Мельников О.И. и др., -М.:Наука, 1990,384 с. 4. Липский В. Комбинаторика для программистов. -М.:Мир,1988, 214с. 5. Современное состояние теории исследования операций / под ред. академика Н.Н. Моисеева. -М.:Наука, 1979. 464 с. 6. Шоломов л.А. Основы теории дискретных логических и вычис-лительных устройств. М.:Наука,1980, 400 с. 7. Кук С.А. Сложность процедур вывода теорем //Кибернетический сборник, вып.12. М.:Мир,1975, с.5-15. 8. Карп Р.М. Сводимость комбинаторных задач //Кибернетический сборник, вып.12. М.:Мир,1975, с.16-38. 9. Левин А.А. Универсальные задачи перебора //Проблемы передачи информации, том 9, №3, 1975, с. 115-116. 10. Сапоженко А.А. Дизъюнктивные нормальные формы. Изд. МГУ, 1975 - 90с.
МЕТОДИЧЕСКОЕ ПОСОБИЕ по дисциплине Теория сложности вычислений для студентов 2 курса дневной (заочной) и экстернатной формы обучения направления 0802 Прикладная математика специальностей 6.080200 Информатика, 6.080200 Прикладная математика Симферополь, 2004 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ АЛГОРИТМИЧЕСКОЙ СЛОЖНОСТИ РЕШЕНИЯ ДИСКРЕТНЫХ ЗАДАЧ Учебно-методическое пособие для студентов факультета математики и информатики
Введение
С появлением компьютеров алгоритмические методы решения задач стали развиваться столь стремительно, что вызвали появление ряда новых, ярких теоретических направлений в математике. К таким направлениям следует отнести теорию сложности решения дискретных задач, основания которой были заложены в работах С. Кука (1971), Р. Карпа (1972) и А.А. Левина (1973) [7-9]. Только после возникновения этой теории (основанной на понятиях NР- полных и NР- трудных задач) многие математики-исследователи осознали бесперспективность поиска эффективных (существенно отличных от переборных) алгоритмов решения многих, важных задач: минимизации дизъюнктивных нормальных форм, задачи целочисленного линейного программирования общего вида, задачи коммивояжера, раскраски графа, нахождения корней полиномов над полем GР(2) и многих других. Оказалось, что указанные задачи являются универсальными переборными задачами в том смысле, что эффективное решение хотя бы одной из них повлечет открытие эффективных алгоритмов решения для всех остальных. В монографии К. Гари и Д. Джонсона [1] приведен список более 300 таких универсальных переборных (NР-полных задач), связанных с теорией графов, математической логикой, алгеброй, дискретной оптимизацией и другими.разделами математики. Изучив теорию NР-полных задач, математик получает на вооружение замечательный аппарат, с помощью которого, приступая и решению новой задачи, во многих случаях можно заранее оценить ее сложность и целесообразность поиска точного алгоритма ее решения за приемлемое число шагов. Теория NР-полных задач достаточно сложна для понимания, и ее изучения основ теории сложности, но для освоения материала понадобится знакомство с теорией функций алгебры логики, теорией алгоритмов, элементами теории графов и исследования операций. Поэтому пособие предназначается, прежде всего, для студентов старших курсов и аспирантов математического факультета. Учитывая важность простых приближенных алгоритмов решения дискретных экстремальных задач и различных эвристических методов, при изучении теории сложности полезно ознакомиться с возможностями алгоритмов «пожирающего» типа (GREEDY). Поэтому в пособии изложены основы теории матроидов и теорема Радо-Эдмондса.
Алгоритм Понятие алгоритма - одно из центральных в математике и, по крайней мере, не менее важное, чем понятие функции. Функция – это соответствие между двумя множествами X и У, согласно которому для каждого элемента Например, функция Лапласа:
полностью определена выражением (1.1) для любого Алгоритм принципиально отличается от функции тем, что устанавливая соответствие Главный элемент, необходимый для строгого определения алгоритма - это набор (множество) элементарных действий, из которых строятся конечные последовательности шагов. Математики, занимавшиеся формализацией понятия алгоритма, предложили pяд способов выбора множества элементарных действий и, соответственно, формальных моделей, уточняющих интуитивное понятие алгоритма. Наиболее удачные формализации понятия алгоритма были разработаны А.А. Марковым (элементарные действия - подстановки), А. Тьюрингом (элементарные действия - команды абстрактной математической машины), Э.Постом, М.Минским. Впоследствии оказалось, что разработанные этими математиками модели алгоритмов эквивалентны в том смысле, что классы решаемых с их помощью задач совпадают. В связи с этим А. Черч сформулировал гипотезу, известную как Тезис Черча, смысл которой состоит в том, что класс задач, решаемых в любой из построенных математиками формальных моделей алгоритмов, и есть класс всех задач, которые могут быть решены “интуитивно алгоритмическими” методами. Для математиков-программистов несложно переписать алгоритм решения задачи, подготовленный на одном языке программирования, на другой язык. Если такая трансляция, скажем, с языка PASCAL на С++ является делом достаточно простым, то трансляция тьюринговского алгоритма в марковский может оказаться значительно сложнее. Но есть одно обстоятельство, которое существенно снижает значение того, в какой формальной или прикладной системе (ЭВМ, язык) записан алгоритм. Пусть в системе | |||||||||||||||||
|
| Поделиться: |

 указывается единственный элемент у=f(x). В ряде случаев оказывается важным не только задать функцию (соответствие) f, но и указать способ нахождения y=f(x) для всякого заданного
указывается единственный элемент у=f(x). В ряде случаев оказывается важным не только задать функцию (соответствие) f, но и указать способ нахождения y=f(x) для всякого заданного  (1.1)
(1.1) , однако способ вычисления по заданному х значения
, однако способ вычисления по заданному х значения  этим выражением не определен.
этим выражением не определен.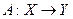 , он определяет не только единственный элемент у =А(х) для всякого
, он определяет не только единственный элемент у =А(х) для всякого  произвольный алгоритм А выполняется за
произвольный алгоритм А выполняется за  шагов; каждый элементарный шаг в системе
шагов; каждый элементарный шаг в системе  может быть представлен эквивалентной последовательностью не более чем из
может быть представлен эквивалентной последовательностью не более чем из  шагов в системе
шагов в системе  . Тогда, заменяя все элементарные действия системы
. Тогда, заменяя все элементарные действия системы  шагов.
шагов. , называют соответственно множествами начальной информации (данных) и финальной информации (результатов). Естественно считать наилучшим тот алгоритм, который позволяет по заданной начальной информации получить правильный результат у=А(Х) за наименьшее по сравнению с другими алгоритмами, решающими эту же задачу в той же самой алгоритмической модели, число шагов.
, называют соответственно множествами начальной информации (данных) и финальной информации (результатов). Естественно считать наилучшим тот алгоритм, который позволяет по заданной начальной информации получить правильный результат у=А(Х) за наименьшее по сравнению с другими алгоритмами, решающими эту же задачу в той же самой алгоритмической модели, число шагов. - тьюринговский алгоритм решения некоторой задачи z из класса Z. Начальная информация (исходные данные) записана на ленте МТ и занимает некоторое количество n ячеек. Это число ячеек называется размером (входа) задачи. Число шагов МТ, выполняемых алгоритмом
- тьюринговский алгоритм решения некоторой задачи z из класса Z. Начальная информация (исходные данные) записана на ленте МТ и занимает некоторое количество n ячеек. Это число ячеек называется размером (входа) задачи. Число шагов МТ, выполняемых алгоритмом  . В процессе выполнения алгоритма изменяется запись на ленте МТ, и головка машины совершает перемещение в пределах участка ленты oт некоторой ячейки
. В процессе выполнения алгоритма изменяется запись на ленте МТ, и головка машины совершает перемещение в пределах участка ленты oт некоторой ячейки  до ячейки
до ячейки  . Этот участок ленты называют рабочей зоной, а длину рабочей зоны
. Этот участок ленты называют рабочей зоной, а длину рабочей зоны 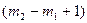 - п ространственной сложностью
- п ространственной сложностью  алгоритма
алгоритма 


 Определение 4.2. Задача Z* называется NР - полной (универсальной переборной задачей), если Z*Î NР и для любой задачи ZÎ NР имеет место полиномиальная сводимость Z µ Z*.
Определение 4.2. Задача Z* называется NР - полной (универсальной переборной задачей), если Z*Î NР и для любой задачи ZÎ NР имеет место полиномиальная сводимость Z µ Z*. µ
µ  , то
, то  , то
, то  Î NР и что Z*µ Z.
Î NР и что Z*µ Z.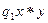 останавливается в конфигурации
останавливается в конфигурации 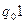 , если свойство R(x, y) выполнено, и в
, если свойство R(x, y) выполнено, и в  - в противнем случае.
- в противнем случае.
 ,
,  - внешний
- внешний ; s - номера ячеек,
; s - номера ячеек,  ; i и j - текущие номера символов алфавитов А и Q,
; i и j - текущие номера символов алфавитов А и Q, 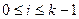 ,
, 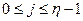 .
. , если на шаге t, обозревая ячейку s,. машина воспринимает символ с номером 1, иначе эта переменная равна нулю;
, если на шаге t, обозревая ячейку s,. машина воспринимает символ с номером 1, иначе эта переменная равна нулю; , если на шаге t машина находится в состоянии с номером j,
, если на шаге t машина находится в состоянии с номером j, , если на шаге t головка машины обозревает ячейку с
, если на шаге t головка машины обозревает ячейку с
 на шаге t машина обозревает хотя бы одну ячейку и при этом
на шаге t машина обозревает хотя бы одну ячейку и при этом


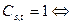 на шаге t в ячейке s записан ровно один символ. Тогда
на шаге t в ячейке s записан ровно один символ. Тогда

 на шаге t машина находится ровно в одном состоянии. Тогда
на шаге t машина находится ровно в одном состоянии. Тогда
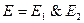




 может иметь не более трех членов, например:
может иметь не более трех членов, например:
 -оптимальное решение, то
-оптимальное решение, то
 , является NР-
, является NР- по крайней мере, столь же сложна.
по крайней мере, столь же сложна. при
при 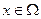 (в этом случае функция принимает не более М - m+1 значений на множестве W), то решить оптимизационную задачу можно путем повторения решения задачи вычисления свойства, выбирая границу В из целочисленного отрезка (m, M). Число шагов решения оптимизационной задачи при таком решении будет в константу раз больше числа шагов решения задачи вычисления свойства. Поэтому оптимизационная целочисленная задача относится к тому классу сложности, что и соот-ветствующая задача вычисления свойства.
(в этом случае функция принимает не более М - m+1 значений на множестве W), то решить оптимизационную задачу можно путем повторения решения задачи вычисления свойства, выбирая границу В из целочисленного отрезка (m, M). Число шагов решения оптимизационной задачи при таком решении будет в константу раз больше числа шагов решения задачи вычисления свойства. Поэтому оптимизационная целочисленная задача относится к тому классу сложности, что и соот-ветствующая задача вычисления свойства. такой, что
такой, что  , если дуга (i,j) имеется в графе Г, и
, если дуга (i,j) имеется в графе Г, и  , если дуги (i,j) в графе Г нет.
, если дуги (i,j) в графе Г нет. называют подграфом графа Г, если
называют подграфом графа Г, если  и
и  .
. верши-нами.
верши-нами. . Начальной
. Начальной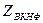 µ
µ 
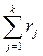 вершин. Пометим для удобства каждую вершину соответствующим ей литералом и порядковым
вершин. Пометим для удобства каждую вершину соответствующим ей литералом и порядковым
 и
и 
 (литералы принадлежат разным скобкам);
(литералы принадлежат разным скобкам); (один литерал не является отрицанием другого).
(один литерал не является отрицанием другого). -набор, на котором
-набор, на котором  Тогда в каждом наборе КНФ Ф найдется хота бы один литерал, обращающийся в единицу. Выберем произвольно по одному такому (обращающемуся в единицу) литералу из каждой скобки. Будет выбрано ровно k литералов. Рассмотрим соответствующие именно этим литералам k вершин графа Г и убедимся, что любая пара из них соединена дугой. Действительно, пометки этих вершин удовлетворяют условиям а) и б), т.к. литералы принадлежат разным скобкам и одновременно принимают единичное значение, поэтому один из них не может быть инверсией другого.
Тогда в каждом наборе КНФ Ф найдется хота бы один литерал, обращающийся в единицу. Выберем произвольно по одному такому (обращающемуся в единицу) литералу из каждой скобки. Будет выбрано ровно k литералов. Рассмотрим соответствующие именно этим литералам k вершин графа Г и убедимся, что любая пара из них соединена дугой. Действительно, пометки этих вершин удовлетворяют условиям а) и б), т.к. литералы принадлежат разным скобкам и одновременно принимают единичное значение, поэтому один из них не может быть инверсией другого.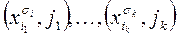
 значения:
значения: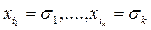 , а остальные переменные,
, а остальные переменные,
 может быть осуществлено с полиномиальной сложностью.
может быть осуществлено с полиномиальной сложностью. F
F 
 -
-


