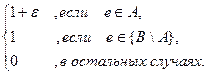Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матроиды и жадные алгоритмы.Содержание книги Поиск на нашем сайте
Рассмотрим следующую задачу. Задача 9.1. Дана матрица с целыми неотрицательными коэффициентами Эквивалентная формулировка этой задачи имеет вид:
Будем решать задачу 9.1, выбирая последовательно элементы из Легко убедиться, что жадный алгоритм правильно решает задачу (9.1). Эта задача является индивидуальной задачей проблемы целочисленного линейного программирования (ЦЛП) с булевыми переменными и ограничениями, задание которых в этом частном случае определяет полиномиальную разрешимость задачи (9.1) со сложностью 0(n). Рассмотрим еще один частный случай задачи ЦЛП. Задача 9.2. Дана матрица коэффициентами. Найти такое подмножество ее элементов, что а) в каждом столбце и в каждой строке находится не более одного выбранного элемента и б) сумма выбранных элементов является макси-мальной. Эквивалентная формулировка задачи:
Попробуем применить жадный алгоритм к задаче (9.3) с матрицей
Выбор наибольшего элемента в первой строке и столбце Рассмотрим более широкий класс задач. Задача 9.3. Дано конечное множество Е, семейство его подмножеств w: Е ® R +; w (е) будем называть: весом элемента еÎ Е. Требуется найти подмножество SÎ J с наибольшей суммой Эквивалентная формулировка задачи:
Определение 9.1. Жадным (пожирающим, GREEDY) называется следующий алгоритм решения задачи (9.4): begin Упорядочить е так, что w(e[1]) >= w(е[2]) >=... >= w(е[n]); S:=Æ; for i:= 1 tо n dо if (S Ç {e[i]}) Î J then S:= S Ç {е[i]}; еnd. Замечание. Для упрощения определения GREEDY алгоритма мы, не теряя общности, считаем, что после упорядочения элементов множества Е они получили имена (и номера) е[1], е[2],..., е[n]. Типичной иллюстрацией частного случая использования GREEDY алгоритма является стратегия «иди в ближайший» для задачи о крат-чайшем пути в графе. Очевидно, что сложность GREEDY алгоритма определяется слож-ностью задачи сортировки n-элементного множества и может быть оце-нена как 0(n). Простота GREEDY алгоритма делает его привлекатель-ным и определяет важность постановки следующей проблемы. Каким условиям, должно удовлетворять семейство J из задачи 9.3. чтобы GREEDY- алгоритм правильно решал эту задачу для произвольной функции w? Оказывается, для решения поставленной проблемы достаточно, чтобы пара <Е,J> образовывала так называемый матроид. Определение 9.2. Матроидом называется пара М=<Е,J>, где Е - конечное множество. J Í 2Е - семейство его подмножеств, удовлетворяющих условиям: М1) пустое множество принадлежит J и, если АÎ J и ВÍ А, то BÎ J; М2) для любых множеств А и В таких, что АÎ J, BÎ J и |В| = |А| + 1, найдется элемент е Î{В \ А} такой, что {АÇ{e}}Î J. Множества семейства J называются независимыми, а остальные множества из { 2E \ J }- зависимыми. Определение 9.3. Максимальным независимым подмножеством множества С Í Е называется такое независимое подмножество А Í С, что не существует независимого множества В, удовлетворяющего включениям: А Ì В Í С. Условия М1) и М2) в определении 9.2 иногда называют аксиомами матроида. Теорема 9.1. Пусть Е - конечное множество, J Í 2Е и J удовлетворяет условию М1. Тогда пара М = <Е,J> является матроидом в том и только том случае, если выполняется условие: МЗ) для произвольного подмножества С Í Е каждые два максимальных независимых подмножества множества С имеют одинаковую мощность. Теорема 9.1 устанавливает эквивалентность аксиом М2 и МЗ матроида. Определение 9.4. Мощность максимального независимого подмножества множества Е называется рангом этого множества;
Очевидно, что подмножество С Í Е является максимальным независимым подмножеством тогда и только тогда, когда r(С) = |C|. Определение 9.5. Каждое максимальное независимое подмножество множества Е из определения матроида М = <Е,J> называется базой этого матроида, а ранг r(E) - рангом матроида. Следствие 9.1. Каждые две базы матроида равномощны. Теорема 9.2. (Радо-Эдмондса) Если м = <Е,J> - матроид, то множество S, найденное GREEDY- алгоритмом при решении задачи 9.3, является независимым множеством с наибольшим весом w: Е ® Ñ+, что множество S, найденное GREEDY- алгоритмом. не будет множеством с наибольшим весом. Доказательство. Пусть М = <Е,J> - матроид и Теперь предположим, что М = <Е,J> не является матроидом. Тогда нарушается хотя бы одна из аксиом матроида М1, М2. Пусть не выполняется М1. Тогда найдутся подмножества А и В такие, что AÎ J, B Í А и BÏ J. Определим функцию w так:
Множество BÏ J не будет содержаться во множестве S, выбранном жадным алгоритмом. Поэтому w(S) < w(B) = w(A). и тогда S не является множеством с максимальным весом. Если же не выполняется аксиома М2, то найдутся множества А Î J и B Î J такие, что |А| = k, |B| = k+1, и для любого eÎ{B\A} будет иметь место {A Ç{e}} Ï J. Обозначим р = |A È B|; р<k. Пусть 0 < ε < 1/(k-р). Определим функцию w так: w(e)= Тогда жадный алгоритм сначала выберет все элементы множества А, затем во всех случаях отбросит элементы множества {B\A}. Будет получено множество S с весом w(S) = w(A) = k(1+ε) которое не будет множеством максимального веса, т.к. вес BÎ J равен w(B) = p(1+ ε) +(k+1- p) ·1 = k + p ε + 1= =k + k ε - k ε + p ε +1 = k(1+ ε)+1- ε (k-p)
Поскольку ε < 1/(k-p) • 1 – ε(k-p) > 0, получаем: w(B) =k(1+ ε) + 1 – ε(k - p) > k(1+ ε) = w(S) Теорема доказана. Таким образом, мы установили, что если в задаче 9.3 (9.4) множество допустимых решений J является набором независимых множеств некоторого матроида <Е,J>, то эта задача легко решается GREEDY-алгоритмом.
Содержание Введение. 3 1. Алгоритмы. 4 2. Класс Р и эффективные вычисления 7 3. Недетерминированные алгоритмы и класс NP 9 4. Класс NР- полных задач 12 5. Теорема Кука: первая NР- полная задача 14 6. Другие NР- полные задачи 21 7. Пример доказательства NР- полноты задачи, методом сведения 24 8. Список NР- полных задач. 27 9. Матроиды и жадные алгоритмы. 28
Список рекомендованной литературы. 1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. -М.: Мир,1982,416 с. 2. Компьютер и задачи выбора. / под ред. академика Ю.И. Журавлева. - М.: Наука, 1989, 207 с. 3. Лекции по теории графов / Емеличев В.А., Мельников О.И. и др., -М.:Наука, 1990,384 с. 4. Липский В. Комбинаторика для программистов. -М.:Мир,1988, 214с. 5. Современное состояние теории исследования операций / под ред. академика Н.Н. Моисеева. -М.:Наука, 1979. 464 с. 6. Шоломов л.А. Основы теории дискретных логических и вычис-лительных устройств. М.:Наука,1980, 400 с. 7. Кук С.А. Сложность процедур вывода теорем //Кибернетический сборник, вып.12. М.:Мир,1975, с.5-15. 8. Карп Р.М. Сводимость комбинаторных задач //Кибернетический сборник, вып.12. М.:Мир,1975, с.16-38. 9. Левин А.А. Универсальные задачи перебора //Проблемы передачи информации, том 9, №3, 1975, с. 115-116. 10. Сапоженко А.А. Дизъюнктивные нормальные формы. Изд. МГУ, 1975 - 90с.
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 837; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

 . Требуется найти такое подмножество ее элементов, что: а) в каждом столбце матрицы содержится не более одного элемента из этого подмножества и б) сумма выбранных элементов максимальна.
. Требуется найти такое подмножество ее элементов, что: а) в каждом столбце матрицы содержится не более одного элемента из этого подмножества и б) сумма выбранных элементов максимальна.
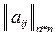 , причем каждый раз - наибольший из оставшихся, проверяя при этом выполнение условия (9.2). Алгоритм такого типа называется жадными или пожирающими (в англоязычной литературе - GREEDY). Жадные алгоритмы похожи на градиентные алгоритмы в численных методах непрерывной математики.
, причем каждый раз - наибольший из оставшихся, проверяя при этом выполнение условия (9.2). Алгоритм такого типа называется жадными или пожирающими (в англоязычной литературе - GREEDY). Жадные алгоритмы похожи на градиентные алгоритмы в численных методах непрерывной математики.

 в искомое подмножество исключает из дальнейшего рассмотрения (в силу заданных ограничений) элементы
в искомое подмножество исключает из дальнейшего рассмотрения (в силу заданных ограничений) элементы 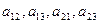 . Поэтому из второго столбца выбирается
. Поэтому из второго столбца выбирается  и затем - из третьего столбца
и затем - из третьего столбца  . Имеем
. Имеем  . Но это решение не экстремальное: подмножество
. Но это решение не экстремальное: подмножество  удовлетворяет ограничениям и
удовлетворяет ограничениям и  .
. (
( - булеан множества Е) и функция
- булеан множества Е) и функция т. е. с наибольшим суммарным весом.
т. е. с наибольшим суммарным весом.
 мно-жество, построенное GREEDY- алгоритмом. Тогда S - база матроида, поскольку каждый элемент
мно-жество, построенное GREEDY- алгоритмом. Тогда S - база матроида, поскольку каждый элемент  , не включенный в S на некотором шаге алгоритма, не может пополнить окончательно построенное множество S без нарушения условия SÎ J. Все базы матроида - максимальные независимые подмножества множества Е - равномощны, поэтому с учетом предварительного упорядочения. элементов множества Е построенное множество S будет иметь наибольший суммарный вес.
, не включенный в S на некотором шаге алгоритма, не может пополнить окончательно построенное множество S без нарушения условия SÎ J. Все базы матроида - максимальные независимые подмножества множества Е - равномощны, поэтому с учетом предварительного упорядочения. элементов множества Е построенное множество S будет иметь наибольший суммарный вес.