
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Введем вспомогательную функциюСодержание книги Поиск на нашем сайте
Пустъ машина обозревает ячейку с номером s, в которой записан символ запись в этой ячейке не изменяется; в противном случае
где выражение в квадратных скобках соответствует тому, что на шаге Т на ленте записаны символы l(пусто) и 1, причем единица содержится не более чем в одной ячейке; сомножитель Приведенные выше выражения позволяют заключить, что формула Ф = В & C & D & Е & F & G, является КНФ, если привести проме-жуточные эквивалентные преобразования:
Ф = 1 равносильно тому, что найдется такое допустимое, значение у, при котором машина, начав работу в конфигурации Если задача z имеет положительный ответ, то для некоторого допустимого у выполнено R(x,y)=1. В этом случае, назначив значения переменных в этом наборе определяют слово у, такое, что машина переводит Очевидно, что длина записи формулы Ф при любом способе ее представления в виде слова над конечным алфавитом ограничена некоторым полиномом от размера входа задачи n, и сведение задачи z к задаче Теорема полностью доказана. Другие NР- полные задачи.
После открытия С. Куком «первой» NР- полной задачи стало воз-можным доказывать NР- полноту других задач, NР- полными оказа- лись: задача выполнимости 3-КНФ, когда в выражении каждая дизъюнкция
задача о вершинном покрытии графа, о существовании гамильтонова цикла в графе, задача коммивояжера в экстремальной постановке, задача целочисленного линейного программирования, задача минимизации дизъюнктивной нормальной формы произвольной булевой функции, задача синтеза бинарного решающего дерева с минимальным числом листьев и многие другие [1]. Важно учитывать, что доказательство NР- полноты всегда произ-водится для любой исходной информации, допустимой для рассматри- ваемой задачи. При этом вполне возможно, что для некоторых исходных данных задача окажется полиномиально разрешимой: известны разрешимые с полиномиальной сложностью частные случаи для задачи минимизации ДНФ монотонной булевой функции, задачи целочис-ленного линейного программирования и многие другие. Задача называется NР- трудной, если к ней полиномиально сводится какая-нибудь NР- полная задача. Класс всех NР- трудных задач обозначают NРН. Задача z Î NРH по крайней мере так же трудна, как и любая задача из NР, но классу NР может не принадлежать. Практическое применение теории NР- полных задач позволяет при изучении каждой новой трудно решаемой задачи определить, целесообразно ли продолжать отыскивать точный эффективный алго-
ритм ее решения. Для этого необходимо установить, принадлежит ли задача классу NРС или NPH. Если такая принадлежность имеет место, то, возможно, имеет смысл искать её приближенное решение, опреде-ляемое следующим образом. Пусть требуется найти экстремум функции f(x) при условии х Î W, Если ε - приближенным называют любое решение х, удовлетворяющее неравенству
Практически важным является выделение подклассов задач из NРС. для которых нахождение ε - приближенных решений позволяет понизить сложность настолько, чтобы перевести решаемую задачу в класс Р. Существенной является и возможность работы с какой - либо одной задачей из NРС для изучения общих подходов к решению; часто в качестве таковой выбирают задачу коммивояжера, задачу минимизации ДНФ. Теория NР - полных задач, как видно из изложенного выше, опе-рирует с задачами вычисления свойств. Поэтому нужно отметить при-менимость теории к дискретным оптимизационным задачам. Если в оптимизационной задаче среди всех структур данного типа ищется структура, имеющая минимальную «стоимость» (например, среди всех маршрутов отыскивается маршрут минимальной длины, как в задаче коммивояжера), то этой задаче можно сопоставить задачу распоз-навания (вычисления) свойства, в котором в качестве дополнительного параметра фигурирует числовая граница В, а вопрос ставится о сущест-вовании структур данного типа, стоимость которых не превосходит В (например, маршрут длины не более В). Задача распознавания не может быть сложнее соответствующей задачи оптимизации. Действительно, имея маршрут минимальной дли-ны и длину этого маршрута, для решения задачи распознавания свой-ства нужно только сравнить ее с заданной границей В. Поэтому если задача вычисления свойства полной, то и задача, Если значения функции f(x) целочисленные и
Пример доказательства NP- полноты задачи методом сведения.
Пусть Г =(Х,U) - конечный граф, Х - множество вершин графа, U - множество дуг. Не теряя общности, можно обозначить вершины натуральными числами: Х = {1,2,..., n}, а дуги задать булевой матрицей Граф называют полным, если любые его две вершины соединены дугой. Граф Задача о полном подграфе состоит в том, чтобы по заданному графу Г выяснить, существует ли в Г полный подграф с Теорема 7.1. Задача о полном подграфе является NP- полной, Доказательство. Для удобства обозначим задачу о полном подграфе информацией о задаче /* Предположим, k-полный подграф существует */ УСПЕХ:= TRUE; /* Недетерминированный выбор k вершин */ Set:= [1..n]; for i:= 1 to k dо begin node:= сhoose(Sеt); v[i]:= node; Set:=Set\(nodе); еnd; /* Полиномиальная проверка */ for i:= 1 tо k-1 do for j:= i+1 tо k dо if u(v[i],v[j])=0 then УСПЕХ:=FALSE; write(УСПЕХ); Очевидно, что сложность приведенной N-программы может быть оценена как О(n(n-1)/2), т.е. полиномиально, откуда следует, что
б) Докажем, что
Пусть
есть произвольная k скобочная КНФ. Поставим во взаимно-однозначное соответствие каждому литералу из Ф вершину некоторого графа Г. Этот граф будет содержать номером скобки, в которую этот литерал входит, т.е. парой
Соединим дугой те, те и только те пары полученных вершин
для которых одновременно выполняются два условия: а) б) Таким образом, построен граф Г =(X,U) с указанными вершинами и дугами. Предположим, - что Ф - выполнима и Обратно, пусть граф Г полный подграф с k вершинами
зададим переменным с номерами
если k < n, зададим произвольно, получая набор
Поскольку эти литералы соответствуют вершинам полного подграфа, то они относятся к разным скобкам КНФ Ф, откуда следует, что Теорема доказана.
Список NР- полных задач.
Ниже приведена лишь небольшая часть задач. NР- полнота кото-рых установлена [1]. Эти задачи могут использоваться для доказа-тельства NР- полноты других задач и представляют известный прак-тический интерес. 8.1. Задача выполнимости КНФ. 8.2. Задача выполнимости 3-КНФ, когда дизъюнкция КНФ содержит не более 3 литералов. 8.3. Задача построения минимальной дизъюнктивной нормальной формы. 8.4. Истинность булевой формулы с кванторами вида
где
один из кванторов " или $. F 8.5. Задача о существовании конечного автомата не более чем с k внутренними состояниями, распознающего заданное подмножество последовательностей. 8.6. Существование бинарного дерева (БРД) решений не более чем с m листьями и задача синтеза БРД с минимальным числом листьев. 8.7. Задача о существовании вершинного покрытия графа мощности k. 8.8. Задача о раскраске графа в k цветов (каждая пара вершин, соеди-ненных дугой, - в разные цвета). 8.9. Задача о существовании гамильтонова цикла в графе и задача коммивояжера. 8.10. Задача распознавания в заданном графе Г1 подграфа, изо-морфного заданному графу Г2. 8.11. Задача о существовании в графе с размеченными дугами разреза с суммой весов дуг не меньшей k. 8.12. Задача о многопроцессорном расписании с заданным дирек-тивный сроком. 8.13. Задача составления учебного расписания. [1, стр. 311]. 8.14. Задача целочисленного линейного программирования, 8.15. Задача о ранце (иногда называется также задачей о рюкзаке). 8.16. Разрешимость квадратных диофантовых уравнений. 8.17. Разрешимость алгебраического уравнения и поле GF(2). 8.18. Задача о покрытии множества не более чем k его подмно- жествами.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |


 , если на шаге t, находясь в состояний
, если на шаге t, находясь в состояний  ,
, ,и смена состояния и записи в ячейке осуществляется в соответствии с программой, причем при отсутствии головки над ячейкой s
,и смена состояния и записи в ячейке осуществляется в соответствии с программой, причем при отсутствии головки над ячейкой s .
.

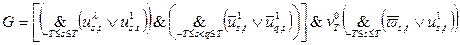
 соответствует нахождению машины на шаге Т в состоянии
соответствует нахождению машины на шаге Т в состоянии  ; последняя конъюнкция обеспечивает условие наличия в обозреваемой ячейке символа 1. '
; последняя конъюнкция обеспечивает условие наличия в обозреваемой ячейке символа 1. '
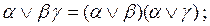
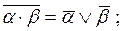

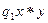 перейдёт в конфигурацию
перейдёт в конфигурацию 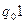 согласно тьюринговской программе полиномиаль-ной проверки.
согласно тьюринговской программе полиномиаль-ной проверки. на основе работы машины над начальной конфигурацией
на основе работы машины над начальной конфигурацией 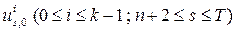
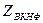 осуществимо за полиномиальное время.
осуществимо за полиномиальное время.
 может иметь не более трех членов, например:
может иметь не более трех членов, например:
 -оптимальное решение, то
-оптимальное решение, то
 , является NР-
, является NР- по крайней мере, столь же сложна.
по крайней мере, столь же сложна. при
при 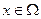 (в этом случае функция принимает не более М - m+1 значений на множестве W), то решить оптимизационную задачу можно путем повторения решения задачи вычисления свойства, выбирая границу В из целочисленного отрезка (m, M). Число шагов решения оптимизационной задачи при таком решении будет в константу раз больше числа шагов решения задачи вычисления свойства. Поэтому оптимизационная целочисленная задача относится к тому классу сложности, что и соот-ветствующая задача вычисления свойства.
(в этом случае функция принимает не более М - m+1 значений на множестве W), то решить оптимизационную задачу можно путем повторения решения задачи вычисления свойства, выбирая границу В из целочисленного отрезка (m, M). Число шагов решения оптимизационной задачи при таком решении будет в константу раз больше числа шагов решения задачи вычисления свойства. Поэтому оптимизационная целочисленная задача относится к тому классу сложности, что и соот-ветствующая задача вычисления свойства. такой, что
такой, что  , если дуга (i,j) имеется в графе Г, и
, если дуга (i,j) имеется в графе Г, и  , если дуги (i,j) в графе Г нет.
, если дуги (i,j) в графе Г нет. называют подграфом графа Г, если
называют подграфом графа Г, если  и
и  .
. верши-нами.
верши-нами. . Начальной
. Начальной
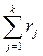 вершин. Пометим для удобства каждую вершину соответствующим ей литералом и порядковым
вершин. Пометим для удобства каждую вершину соответствующим ей литералом и порядковым
 и
и 
 (литералы принадлежат разным скобкам);
(литералы принадлежат разным скобкам); (один литерал не является отрицанием другого).
(один литерал не является отрицанием другого). -набор, на котором
-набор, на котором  Тогда в каждом наборе КНФ Ф найдется хота бы один литерал, обращающийся в единицу. Выберем произвольно по одному такому (обращающемуся в единицу) литералу из каждой скобки. Будет выбрано ровно k литералов. Рассмотрим соответствующие именно этим литералам k вершин графа Г и убедимся, что любая пара из них соединена дугой. Действительно, пометки этих вершин удовлетворяют условиям а) и б), т.к. литералы принадлежат разным скобкам и одновременно принимают единичное значение, поэтому один из них не может быть инверсией другого.
Тогда в каждом наборе КНФ Ф найдется хота бы один литерал, обращающийся в единицу. Выберем произвольно по одному такому (обращающемуся в единицу) литералу из каждой скобки. Будет выбрано ровно k литералов. Рассмотрим соответствующие именно этим литералам k вершин графа Г и убедимся, что любая пара из них соединена дугой. Действительно, пометки этих вершин удовлетворяют условиям а) и б), т.к. литералы принадлежат разным скобкам и одновременно принимают единичное значение, поэтому один из них не может быть инверсией другого.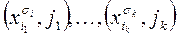
 значения:
значения: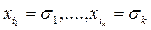 , а остальные переменные,
, а остальные переменные,
 может быть осуществлено с полиномиальной сложностью.
может быть осуществлено с полиномиальной сложностью. F
F 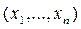
 -
-


