Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Кука: первая NР - полная задачаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исторически первой задачей, для которой С. Куком [7] было дано доказательство NР - полноты, была задача выполнимости КНФ (конъюнктивной нормальной, формы). КНФ называется формула вида
Задача выполнимости состоит в том, чтобы по заданной КНФ узнать, обращается ли реализуемая ею функция алгебры логики в единицу хотя бы на одном наборе Теорема_5.1. (Сoоk S.A., 1971). Задача выполнимости КНФ является NР- полной. Доказательство: Достаточно убедиться, что: а) б) что любая задача из NР полиномиально сводится к а) Недетерминированный алгоритм, решающий задачу
-недетерминированным оператором выбрать - просмотреть в каждой из m скобок не более, чем n значений
Очевидно, для этого недетерминированного алгоритма сложность может быть оценена как o(mn) и является полиномиальной, поэтому
б) Покажем, что любая задача из NP полиномиально сводима к
Сначала отметим, что любая задача вычисления свойств может быть представлена следующим образом: по заданному объекту х, выяснить, существует ли объект у такой, что R(x,y)=1. В нашей задаче объект х - формула, а у - набор значений переменных. Свойство R(x,y) состоит в том, что на наборе у формула х выполнима. Любая задача из NP может быть сформулирована как задача вычисления свойства. Суть дальнейшего доказательства состоит в указании процедуры, которая для любого полиномиального недетерминированного алгоритма вычисления свойства (выходом которого являются ответы «истина» или «ложь») и для любой допустимой начальной информации такого алгоритма строит одно логическое выражение в виде КНФ, которое является выполнимым тогда и только тогда, когда алгоритм определяет ответ «истина», причем построение этого логического выражения из формального описания недетерминированного алгоритма и его входной информации можно выполнить за полиномиальное число шагов. Построение этой процедуры выполняется в терминах алгоритмической системы Тьюринга. Итак, произвольная задача z вычисления свойства R(x,y) из
класса NР может быть выполнена на НДМТ с полиномиальной проверкой, т.е. за число шагов, ограниченное полиномом от размера задачи l(х)+l(y) = n. Полиномиальной при этом будет и длина рабочей зоны ленты НДМТ Т = Р(n) P(,) - некоторый полином, ячейки НДМТ обозначим целочисленными номерами.... -2, -1, 0,+1,+2,.... Расположение начальной информации на ленте представлено на рис. 5.1. в ячейках с номерами 1,……, n
начальная информация Рис. 5.1 Вычисления при любом допустимом значении объекта у происходят в зоне ленты [-Т, Т] и завершаются не более чем за Т шагов (тактов работы НДМТ). Машина начав работу в конфигурации Построим КНФ Ф, такую, что любая задача проверки (распознания) свойства - в общем виде: - полиномиально сводится к проверке выполнимости КНФ Ф = В & C & D & Е & F & G, где В, С, D, E, f, g - дизъюнкты, имеющие следующий смысл: В = 1 • на каждом шаге головка машины обозревает ровно одну ячейку ленты:
С = 1 • в каждой ячейке на каждом шаге записан в точности один символ; D = 1 • на каждом шаге работы машина находится ровно в одном состоянии; Е = 1 • начальная конфигурация машины имеет вид F = 1 • машина работает по тьюринговской программе; G = 1 • заключительная конфигурация машины имеет вид если Р(х,у) = 1. Обозначим и внутренний алфавиты НМДТ; t - шаги выполнения алгоритма,
Введем следующие логические переменные:
иначе эта переменная равна нулю.
номером s, иначе эта переменная равна нулю. Используя введенные логические переменные, можно записать в виде формул следующие логические условия;
никакие две одновременно, т. к. Тогда
В начальном положении (t=0) головка машины обозревает ячейку с номером 1 в состоянии q1, а в первых n - ячейках записаны символы слова Х = х(1)...х(n), за ним - разделительный знак «*», после чего - слово Y и далее - пустые ячейки. Выполнение такой начальной конфигурации равносильно Е = 1, где
где l - пустой символ. Полиномиальная программа проверки свойства состоит из тьюринговских команд:
|
|||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |


 (5.1)
(5.1) значений переменных
значений переменных  . Будем обозначать эту задачу
. Будем обозначать эту задачу 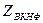 .
. и
и ;
; литералов
литералов 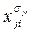 и дать ответ «выполнима», если в каждой скобке найдется хотя бы один литерал, принимающий значение 1, иначе дать ответ «не выполнима».
и дать ответ «выполнима», если в каждой скобке найдется хотя бы один литерал, принимающий значение 1, иначе дать ответ «не выполнима». произвольное начало отсчета
произвольное начало отсчета

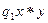 останавливается в конфигурации
останавливается в конфигурации 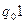 , если свойство R(x, y) выполнено, и в
, если свойство R(x, y) выполнено, и в  - в противнем случае.
- в противнем случае.
 ,
,  - внешний
- внешний ; s - номера ячеек,
; s - номера ячеек,  ; i и j - текущие номера символов алфавитов А и Q,
; i и j - текущие номера символов алфавитов А и Q, 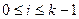 ,
, 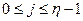 .
. , если на шаге t, обозревая ячейку s,. машина воспринимает символ с номером 1, иначе эта переменная равна нулю;
, если на шаге t, обозревая ячейку s,. машина воспринимает символ с номером 1, иначе эта переменная равна нулю; , если на шаге t машина находится в состоянии с номером j,
, если на шаге t машина находится в состоянии с номером j, , если на шаге t головка машины обозревает ячейку с
, если на шаге t головка машины обозревает ячейку с
 на шаге t машина обозревает хотя бы одну ячейку и при этом
на шаге t машина обозревает хотя бы одну ячейку и при этом


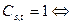 на шаге t в ячейке s записан ровно один символ. Тогда
на шаге t в ячейке s записан ровно один символ. Тогда

 на шаге t машина находится ровно в одном состоянии. Тогда
на шаге t машина находится ровно в одном состоянии. Тогда